#Javaで学ぶアルゴリズム < テイラー展開 >
はじめに
Javaは授業で触れただけで全くの初心者であり,何もわかっていない.なので,基本的なアルゴリズムをJavaで実装し,アルゴリズムの理解を深めるとともに,Javaにも慣れていきたい.
その第9弾としてテイラー展開を扱う.
テイラー展開
テイラー展開は,近似的に式の値を求めることによく用いられる数学的手法の1つである.以下に例を示す.※テイラー展開としているが,厳密にはマクローリン展開である.マクローリン展開については後述する.
例①:exp(x)
$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^{k-1}}{(k-1)!}+\frac{k}{k!}+...$
例②:cos(x)
$cos(x)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+...$
実装
ここでは,$e^x (x\ge0)$と$e^x (x\le0)$と$cos(x)$を例に実装する.ここで,プログラムを組むにあたって,先ほどの式に説明を加える.次にそれを示す.
$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^{k-1}}{(k-1)!}+\frac{k}{k!}+...$
$\ \ \ \ \ \ \ \ |------d------|$
$\ \ \ \ \ \ \ \ |-------s-------|$
$d$: $(k-1)$項までの和
$s$: $k$項までの和
この式は無限級数であるから,実際の計算においては,有限回で打ち切らなければならない.打ち切る条件は,$k-1$項までの和を$d$,$k$項までの和を$s$としたとき,$\frac{|s-d|}{|d|}<EPS$となったときである.
$|s-d|$を打ち切り誤差,$\frac{|s-d|}{|d|}$を相対打ち切り誤差という.$EPS$は許容範囲であり,必要な精度に応じて適当に設定する.
ここから,ソースコードとそのときの出力を示す.
ソースコード①:exp(x)
//2021/03/03
//@Yuya Shimizu
//-------------------------------
//* テイラー展開(exp(x)) *
//-------------------------------
import java.awt.*;
import java.awt.event.*;
//パネルの設定
class taylor1_Panel extends Panel{
double myexp(double x){
final double ESP = 1e-08; //許容誤差
double s = 1.0, e = 1.0, d = 1.0; //テイラー展開の初期値(初項)
int k;
for (k=1; k<=200; k++){
d = s; //(k-1)項までの和
e = e*x/k; //k番目の項
s = s + e; //k項までの和
if (Math.abs(s - d) < ESP*Math.abs(d)){ //打ち切り誤差
return s; //k項までの和をテイラー展開値として出力
}
}
return 0.0; //収束しないとき
}
//表示
public void paint(Graphics g){
double x;
g.drawString(" x myexp(x) exp(x)", 0, 20);
for (x=0; x<=40; x=x+10){
g.drawString(""+x, 20, (int)x*2+40);
g.drawString(""+myexp(x), 80, (int)x*2+40);
g.drawString(""+Math.exp(x), 260, (int)x*2+40);
}
}
}
//フレームの設定
class taylor1_Frame extends Frame{
public taylor1_Frame(){
setSize(450, 200);//450×200の大きさでフレームを作成
//×ボタンを押したら終了
addWindowListener(new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}
});
Panel p = new taylor1_Panel(); //パネルオブジェクトpに先ほど設定したパネルを指定
add(p); //フレームにそのパネルを貼り付け
}
}
//クラス
public class taylor1{
//メイン関数
public static void main(String[] args){
Frame w=new taylor1_Frame();
w.show();
}
}
出力
上記のプログラムでは,負の値に対応できない.
ソースコード②:exp(x)--負の値に対応
//2021/03/03
//@Yuya Shimizu
//-------------------------------------------------------
//* テイラー展開(exp(x)改良版): 負の場合にも対応 *
//-------------------------------------------------------
import java.awt.*;
import java.awt.event.*;
//パネルの設定
class taylor2_Panel extends Panel{
double myexp(double x){
final double ESP = 1e-08; //許容誤差
double s = 1.0, e = 1.0, d = 1.0, a; //テイラー展開の初期値(初項)
int k;
a = Math.abs(x);
for (k=1; k<=200; k++){
d = s; //(k-1)項までの和
e = e*a/k; //k番目の項
s = s + e; //k項までの和
if (Math.abs(s - d) < ESP*Math.abs(d)); //打ち切り誤差
if (x > 0)
return s; //k項までの和をテイラー展開値として出力
else
return 1.0/s; //k項までの和が負値⇒逆数をテイラー展開値として出力
}
return 0.0; //収束しないとき
}
//表示
public void paint(Graphics g){
double x;
g.drawString(" x myexp(x) exp(x)", 0, 20);
for (x=-40; x<=40; x=x+10){
g.drawString(""+x, 20, (int)(x+40)*2+40);
g.drawString(""+myexp(x), 80, (int)(x+40)*2+40);
g.drawString(""+Math.exp(x), 260, (int)(x+40)*2+40);
}
}
}
//フレームの設定
class taylor2_Frame extends Frame{
public taylor2_Frame(){
setSize(450, 250);//450×250の大きさでフレームを作成
//×ボタンを押したら終了
addWindowListener(new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}
});
Panel p = new taylor2_Panel(); //パネルオブジェクトpに先ほど設定したパネルを指定
add(p); //フレームにそのパネルを貼り付け
}
}
//クラス
public class taylor2{
//メイン関数
public static void main(String[] args){
Frame w=new taylor2_Frame();
w.show();
}
}
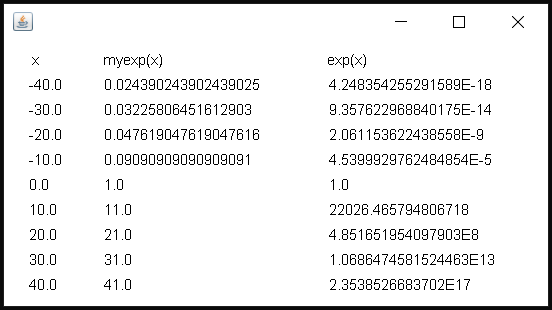
出力
ソースコード③:cos(x)
//2021/03/03
//@Yuya Shimizu
//-------------------------------
//* テイラー展開(cos(x)) *
//-------------------------------
import java.awt.*;
import java.awt.event.*;
//パネルの設定
class taylor3_Panel extends Panel{
double mycos(double x){
final double ESP = 1e-08; //許容誤差
double s = 1.0, e = 1.0, d = 1.0; //テイラー展開の初期値(初項)
int k;
x = (x - (int)x + (int)x%360) * 3.1415927/180; //xの値を0~2πに納める
for (k=1; k<=200; k++){
d = s; //(k-1)項までの和
e = -e*x*x/(k*(k+1)); //k番目の項
s = s + e; //k項までの和
if (Math.abs(s - d) < ESP*Math.abs(d)); //打ち切り誤差
return s; //k項までの和をテイラー展開値として出力
}
return 9999.0; //収束しないとき
}
//表示
public void paint(Graphics g){
double x;
g.drawString(" x mycos(x) cos(x)", 0, 20);
for (x=0; x<=180; x=x+10){
g.drawString(""+x, 20, (int)x*2+40);
g.drawString(""+mycos(x), 80, (int)x*2+40);
g.drawString(""+Math.cos(x*3.1415927/180), 260, (int)x*2+40);
}
}
}
//フレームの設定
class taylor3_Frame extends Frame{
public taylor3_Frame(){
setSize(450, 450);//450×450の大きさでフレームを作成
//×ボタンを押したら終了
addWindowListener(new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}
});
Panel p = new taylor3_Panel(); //パネル変数
add(p);
}
}
//クラス
public class taylor3{
//メイン関数
public static void main(String[] args){
Frame w=new taylor3_Frame();
w.show();
}
}
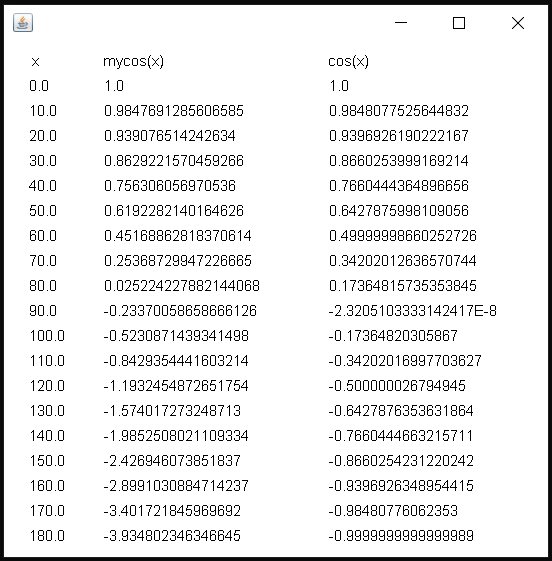
出力
マクローリン展開
まず,$f(x)$の$x=a$におけるテイラー展開を示す.
$f(x)=f(a)+f'(a)\frac{x-a}{1!}+f''(a)\frac{(x-a)^2}{2!}+...$
$a=0$のときのテイラー展開を特にマクローリン展開という.つまり,マクローリン展開はテイラー展開の特殊な場合ということである.マクローリン展開の式を次に示す.
$f(x)=f(0)+f'(0)\frac{x}{1!}+f''(0)\frac{x^2}{2!}+...$
これで,上で示していた例は厳密にはマクローリン展開であることが理解できる.
桁落ち
例えば,有効桁数8桁で,$1234567.7+0.14556-1234567.9$という計算を考えてみる.
$1234567.7+0.1456\approx1234567.8$(有効桁数8)となり,真値($1234567.8456$)に対して大きな誤差はないが,$1234567.8-1234567.9=-0.1$となり,真値($-0.0544$)に対して,約50%もの誤差となる.
このように,上位の正しい桁が減算によりなくなった場合,それまで小さかった誤差が相対的に増大してしまう現象を桁落ちという.ここでは,はじめの2項を計算した時点で有効桁数に従い,無視した$0.0456$の部分が,3項目との計算時に上位の数字が減算によりなくなったことにより,相対的に大きくなったということである.
感想
テイラー展開とマクローリン展開の復習ができた.また,桁落ちについての理解も改めて深まった.
参考文献
Javaによるはじめてのアルゴリズム入門 河西 朝雄 著 技術評論社