決定木を学ぶ

はじめに

決定木は一連の判断に基づいて決定を下すというモデルです。
RPGの選択肢によって分類する感じのあれですね。

手法

・情報利得が最大となる特徴量でデータを分割する。
・この分割を条件分岐ごとに繰り返す。
・分割されたデータが純粋になるまで繰り返す

という手法です。
完全に分割されるまでやると過学習に陥りやすいので深さには制限を設ける場合がおおいです。

情報利得の定義

情報利得はInformation GainらしいのでIGというように定数化されることが多みたいです。
IGは以下のように定義されます。

IG(D_p, f) = I(D_p) - \sum_{j=1}^{m} \frac{N_j}{N_p}I(D_j) \\

f: 分割を行う特徴量\\
D_p:親のデータセット\\
D_j:j番目のデータセット\\
N_p:親データ数\\
N_j：子データ数\\
I:不純度

不純度は何らかの指標なので一旦何らかの数値とすることにします。すると親の不純度から、子の不純度を引いたものが情報利得となります。

ここで一旦理解のために親ノード１に対して子ノードが二つ(子ノード１、子ノード２)に別れた場面を想定します。

IG(D_p, f) = I(D_p) - \sum_{j=1}^{m} \frac{N_j}{N_p}I(D_j) \\
=  I(D_p) - (\frac{N_1}{N_p}I(D_1) + \frac{N_2}{N_p}I(D_2) )\\

D_1:子ノード１のデータセット\\
D_2:子ノード2のデータセット\\
N_p:親データ数\\
N_1：子ノード１のデータ数 \\
N_2：子ノート２のデータ数 \\

つまり、情報利得は、子ノードの不純度の合計が最小になるような特徴量を選択することが目的となるような指標なのです。

不純度

では不純度とは一体なんのか。

よく使用される不純度の指標は

• ジニ不純度
• エントロピー
• 分類誤差

です。

　ジニ不純度

I_G(t) = \sum_{i=1}^{c} P(i|t)(1 - p(i|t)) = 1 - \sum_{i=1}^{c} P(i|t)^2 \\

P(i|t): ノードtでクラスiに属する割合\\

よってIは　0〜１をとりえます。
このジニ不純度が最小である０になるのはP(i|t)が１になる時です。つまり完全に分類され切った時になります。
逆に最大になるのは、P(i|t)=0.5の時です。２分類となった時、片方のノードに全てのデータが振り切られたのであれば、

I_G(t) = \sum_{i=1}^{c} P(i|t)(1 - p(i|t))　= 1 - ( 1 + 0 ) = 0

となります。

エントロピー

I_H(t) = -\sum_{i=1}^{c} P(i|t)log_2 P(i|t)\\

P(i|t): ノードtでクラスiに属する割合\\

こちらもさっきと同様にP(i|t)が１になった時、エントロピーが０になります。

I_H(t) = -\sum_{i=1}^{c} P(i|t)log_2 P(i|t) = -(log_2 1 + 0)= -(0 + 0) = 0 \\

になります。

分類誤差

I_E(t) = 1 - max\{ P(i|t) \}

こちらはすごく単純に、子ノードのラベルの最大値が大きいものの割合を１から引いたものになります。
つまり、

ラベル１：20
ラベル２：３０

あったとするなら

p(1|t) = 20 / 50 =  \frac{2}{5}\\
p(2|t) = 30/50 = \frac{3}{5} \\

なので

I_E(t) = 1 - \frac{3}{5}

となります。
これも同じようにp(i|t)=1となればI_E(t) = 0 になります。

敏感度

３つ不純度を表すための手法があるんですが、それぞれ推定するため不純なものが入っていることを検知するための度合いがことなります。

分類誤差　＜　ジニ不純度 < エントロピー

という順番に検知能力が異なります。

決定木の構築

scikitlearnを使った場合DecisionTreeClassifierを使うと行うことができます。

結果としてはこんなものができあがるんですが、じゃあ一体、この閾値ってどう決めてるの？
とか、よくわからないので深追いして行きましょう。

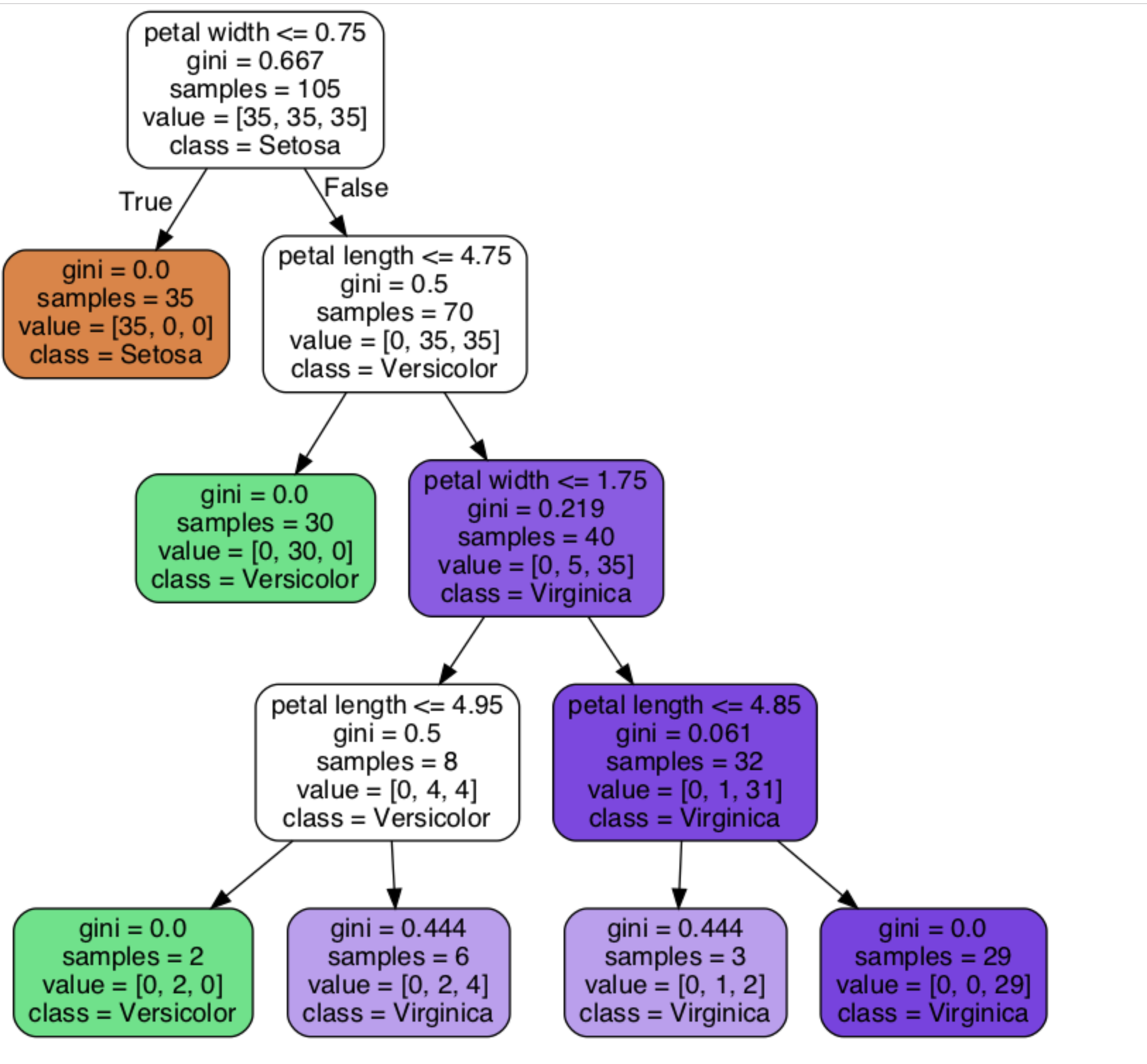
ですが、それ使っちゃうとそれまでになるので、詳細なアルゴリズムをおって行きます。

決定木アルゴリズムを実装してみる
を参考にさせていただきました。。

決定木を具体的に決めるためにはどうやって決めるか。

結局のところ、情報利得が最大になるような分割をすればいいと言ってしまえばそこまでなんですが、実際にはどうやっているのかを僕なりに咀嚼して書きます。
この記事では、情報利得(IG)というものが出てきました。情報利得は親の不純度から、子の不純度を引いたもので、うまく分割できているほど大きくなると言う寸法でした。

計算手順

• 1.特徴量をランダムに決定する。
• 2.各特徴量のユニークな値を求め、中間値を求め、閾値とする。
  • [1,2,3,4]　であれば、[1.5, 2.5, 3.5]となる。
• 3.2で求まった閾値を元にそれぞれ分割を行う。
• 4.3で分割されたノードを元にIGを算出。
• 5.全ての閾値ごとに行い、もっともIGの高い閾値を採択（閾値の比較）
• 6.全ての特徴量で同じように計算を行い、もっともIGの高い特徴量を算出（特徴量の比較）
• 7.規定の深さになるまで演算を繰り返す

という

ランダムフォレスト

よく使われる。取り合えずやっとけという声もよく聞く。
アンサンブル学習という学習法を取り入れた決定木です。

アンサンブル学習

３人寄れば文殊の知恵とはよくいったものでそれを体現した学習方法です。
複数のモデルを作り、それらを多数決で組み合わせたモデルを作ります。
故に、学習できてない、学習しすぎという問題について緩和することができます。
この詳細はおいおい！。

ランダムフォレストでは、

• 1.データを復元抽出
• 2.抽出した標本から、特徴量を非復元抽出
• 3.抽出した特徴量を使って分割を行う
• 4.一定数1-3を繰り返し、多数決でモデルを作成する

という方法。
一般的にはノイズ混みのデータにも強い。