Go to Qiita Advent Calendar 2024 Top
LoginSignup
41
33

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

MATLAB/SimulinkAdvent Calendar 2021Day 16
@YutaNakamurajp(Yuta Nakamura)

MATLABを使った卒論・修論・論文向けグラフ作成方法まとめ（補助線・2軸グラフ・疑似カラープロット・アノテーション・拡大図の書き方etc）

Last updated at Posted at 2021-12-15

はじめに

12月も半ばとなり、卒論・修論の時期ですね。皆さんは進捗いかかでしょうか。もう執筆終わった、半分くらい終わった、とりあえず書くための結果が出た、論文構成だけできた、（頭の中では）とっくに終わった・・・など、人それぞれかと思います。

今回はMATLABを使った卒論や修論、また論文にも使えるようなグラフの作成方法についてまとめました。既に論文書いたという人も参考になれば幸いです。

この記事で作成できるグラフ例

この記事でこんなグラフを作成することができます。サンプルコードはこちらで公開しています。

グラフ例1
Result.jpg

グラフ例2
Color.jpg

グラフ例3

2axes.jpg

留意点

ここで挙げるグラフ作成方法はあくまでも一般的な内容であり、分野や研究室（先生）によって推奨されない部分もありますので、自分の関連分野の論文の図と併せて参考にしてください（結構重要だったりします）。

関連内容

参考にした文献は末尾にまとめていますが、関連する記事も踏襲しているつもりです。

動作環境

Windowsで動作検証していますが、Macでも動作すると思います。

プログラムと結果ファイルの構成

グラフの作成方法について説明する前に、個人的におすすめする結果（データ）の管理方法について説明しておきます。ここでしっかり整理しておくと、グラフ作成が比較的楽にできます。特に学生の方は下記について一読ください。

結果ファイルの管理の重要性 多くの研究・論文では、既に開発されている手法と論文で提案あるいは開発した手法等の、複数の結果で比較するかと思います。各結果のデータが少なければ管理にそれほど注力する必要はありませんが、各結果を計算するためのプログラム複雑になってくると、再計算するとき、また卒業して後輩に引き継ぎする際に後悔するので、面倒がらずに管理にも気を使いましょう。
結果ファイルの管理方法例 例えば、以下のようなフォルダ構成を作り、その中でプロジェクト(prj)ファイルやgitを作成させます。MATLABにおけるgitを用いた管理や共有方法については[Projectによる継続的なチーム開発の実現](https://jp.mathworks.com/videos/continuous-team-development-using-project-1638877903151.html)にまとめられています。また、それぞれの計算に共通するパラメータ変数をaとすると、a=1、 a=2の結果に対応する名前がわかるように、フォルダあるいはmatファイルを作成しておくと良いでしょう。プログラム実行時に自動で結果ファイルを作成・結果を格納する方法は[こちら](https://qiita.com/bbhomejp/items/fac60f397685f6fb8050)を参考にしてください。rootフォルダ以下を1つのプロジェクトとするか、input.mat（入力・設定）ファイルを作成するかは、プログラムの規模で変わってくるので、好きに変えてください。ただし、重要なことはグラフに使用する結果（mat）ファイルまでの構成・変数名を統一したルールに従っていることですので、そこからは逸脱しないようにしましょう。また、+Functionフォルダの"+"は パッケージ フォルダーを特定するために使っています（詳細は[パッケージによる名前空間の作成](https://jp.mathworks.com/help/matlab/matlab_oop/scoping-classes-with-packages.html)参照）。
フォルダ例
root/
 ├+Function/  
        ├+ZoomPlot/   %拡大グラフ作成パッケージ(3.3にて解説)
           ├BaseZoom.m 　%拡大グラフ作成関数(3.3にて解説)
 ├graph.mlx  %グラフ作成プログラム
 ├ Conventional/  %従来手法プログラムフォルダ（ケース名）
        ├ Conventional.prj  %従来手法プロジェクト
        ├ calculation.mlx  %従来手法計算プログラム
        ├ result/       %従来手法計算結果フォルダ
　　　　　　 ├ a_1/       %a=1の結果フォルダ
          　　 ├ input.mat %入力matファイル
          　　 ├ result.mat %結果matファイル
　　　　　   ├ a_2/       %a=2の結果フォルダ
        　　　 ├ input.mat %入力matファイル
        　　　 ├ result.mat %結果matファイル
  ├ Proposed/    %提案手法プログラムフォルダ（ケース名）
        ├ Proposed.prj  %提案手法プロジェクト
        ├ calculation.mlx  %提案手法計算プログラム
      　├ result/　　  %提案手法計算結果フォルダ
　　　　　　 ├ a_1/       %a=1の結果フォルダ
        　　　 ├ input.mat %入力matファイル
        　　　 ├ result.mat %結果matファイル
　　　　　   ├ a_2/       %a=2の結果フォルダ
        　　　 ├ input.mat %入力matファイル
        　　　 ├ result.mat %結果matファイル

次項では本題である、ルートフォルダ直下にあるgraph.mlxでのグラフの書き方について説明していきます。

グラフ作成用プログラム

これから本題に入ります。まず、このプログラム(graph.mlx)は「それぞれの結果データを取得し、グラフを書くためのプログラム」であり、基本的に計算はしません。1つの論文に対して1つのプログラムとし、同じデータであってもグラフのテンプレ等が違うので「卒論用」と「学会発表用」など、わけるようにすると良いでしょう。（私は研究ミーティング単位でグラフ用プログラムファイルを作成しています）。
ライブスクリプト上でコーディングしてグラフを作成すると、ちょっとした打合せなどであれば「コードを非表示」でグラフだけを見せることもできますし、PDF/Word/LaTex/Markdown (livescript2markdown 関数を使用)などにもエクスポートできます。

タイトルと見出し

まずタイトルですが、ライブスクリプトを新規作成した後、"#"を打ち 「グラフ作成プログラム」等と入力し、Enter で入力しましょう。ライブスクリプトでは見出しが見出し1～3まで用意されており、Markdown記法のように書くことができますので、

  • 見出し1(##):論文の章や節
  • 見出し2(###):大きな分類（例：入力データ、特定のパラメータの結果、など）
  • 見出し3(####):1つのグラフ（図）
    としておくと、目次にしたときにわかりやすいかと思います。見出しの切り替えは"#"をレベルの数で変わりますが、文字を入力した後の変更は ctrl+shift+1(2,3) が便利です。また、1つのグラフにつき1つのセクションにしておくと、1グラフ単位の実行も容易になります。グラフの順番は章や節といった論文におけるグラフの順序に合わせると、後々管理が楽です。

0.データの読み込み

最初に「データ読み込み」などの見出しを作り、各データの結果を読み込みましょう。このとき、1つのcell配列かstruct配列にしておくと良いでしょう。ここでは，"ResCell"を作成し，1行目にケース名（"Conventional","Proposed") ，2行目に入力データ，3行目に出力データとします。

clear; %プログラム初期化

CaseName={'Conventional','Proposed'}; %ケース名
nCase=size(CaseName,2);

ResCell=cell(3,nCase);  %結果を格納するcell配列
ResCell(1,:) =CaseName;            %1行目:ケース名

Path = fullfile(CaseName, 'result'); %フォルダのパス名取得

for iCase=1:nCase
	List = dir(Path{iCase});        %各ケースのフォルダの情報取得
 folderName ={List(3:end).name};  %各ケースの結果フォルダ名（例ではa_1など）
 FolderPath ={List(3:end).folder};%各ケースの結果フォルダパス
 %各ケースにある各フォルダ（a_1,a_2）の読み込み
 for iFolder =1: length(FolderPath)
     % 入力データ
     ResCell{2,iCase}.(string(folderName(iFolder)))=load(fullfile(FolderPath{iFolder},folderName{iFolder},'input/input.mat'));
     % 結果データ
     ResCell{3,iCase}.(string(folderName(iFolder)))=load(fullfile(FolderPath{iFolder},folderName{iFolder},'output/result.mat'));
 end
end

cell配列じゃなくて構造体が良い人は以下で変換するのもありです。上のコードはcell2structでの変換を意識したものになっておりますので、cell配列の行方向に対するフィールド名をオプション指定すれば簡単に構造体に変換できます。

% 構造体に変換
ResStruct= cell2struct(ResCell,{'CaseName','InputData','ResultData'});

また必要に応じて配列（ResCellまたはResStruct） をmatファイルに保存しましょう。

save('ResCell.mat','ResCell');    %cell配列
save('ResStruct.mat','ResStruct'); %構造体

こうすると各ケース・各パラメータと結果の対応関係が明確になります。ただし、グラフを書くたびに上記を実行する必要はありません（公開しているプログラムはmatファイルがない場合のみ実行します）。

グラフの設定手順

やっと(?)本題です。グラフは

  1. データのプロット：グラフにするデータの指定・軸や凡例の追加
  2. 共通事項（基本設定）：同一のサイズ・型・フォントの設定
  3. （必要に応じて）アノテーション・拡大図の追加
  4. グラフの出力：ファイル出力、クリップボードへコピー等

の順番に書くようにします。

例を使って説明します。

1.データのプロット

ここではplot関数を用いてプロットしますが、オプションの指定は関数で指定する方法とハンドルを用いてプロパティから指定する方法があります。ハンドルを用いた場合のイメージはこちらに記載されています。

データのプロット
clf;
figure();

p1=plot(ResCell{3,1}.a_1.y,'--k'); %プロット（線種・色を一括指定する場合）
hold on %グラフの追加
p2=plot(ResCell{3,2}.a_1.y);       %プロット（Lineプロパティで指定する場合）
p2.LineStyle='-';
p2.Color=[0,0,0];
hold off
1-1.jpg

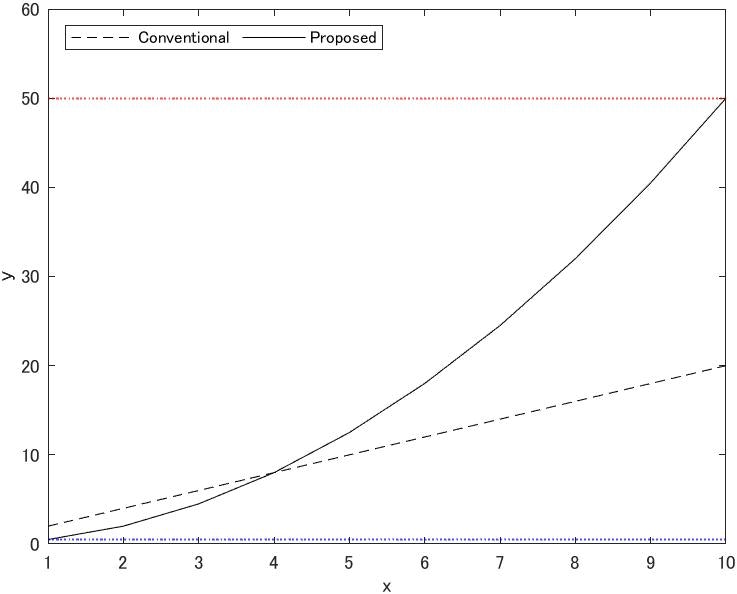
補助線（x,y平行線)

場合によって補助線を引くことがあるでしょう。x軸またはy軸に平行な線はxline、ylineを使います。ここでは、最大値と最小値に異なる色で線を引きます。線の太さは'LineWidth'(標準=0.5)で設定できます（線種が点線 ':'だと線が見えにくいのでいつも太めにしています） .なお、2つのプロパティを一括して設定したい場合は、コンマ区切りリストとdeal関数を用いると1行で書けます。

補助線（x,y平行線)
maxY=max([ResCell{3,1}.a_1.y;ResCell{3,2}.a_1.y],[],"all");　%y軸平行線の高さ(最大値)
minY=min([ResCell{3,1}.a_1.y;ResCell{3,2}.a_1.y],[],"all");  %y軸平行線の高さ(最小値)

yl=yline([maxY,minY],':','LineWidth',1.0);  % 2本のy軸補助線 (線種のみ一括指定）
[yl.Color]=deal([1,0,0],[0,0,1]); % 2本のy軸補助線 (色を個別に指定）
1-2.jpg

x,y軸のラベルとグラフ領域

x軸・y軸のラベルを付け、グラフ領域（x,y軸の上下限）を設定します。

x,y軸のラベルとグラフ領域
xlabel('x');
ylabel('y');
xlim([1 10]);
ylim([0 60]);

凡例

凡例はlegend関数で作成できます。また、ハンドルを指定することで必要な項目を限定することができます。
凡例の場所と列数は、"location"と"NumColumns"で指定しておくと便利です。

凡例
legend([p1;p2],{ResCell{1,:}},"Location","northwest","NumColumns",2);

※legend関数だけでないですが、オプション 'Interpreter'を'tex'と指定するとギリシャ文字などの特殊文字も扱うことができます（下記に例あり）。

1-3.jpg

2軸グラフ

2軸グラフは yyaxis right, yyaxis left と変えることでそれぞれの軸のグラフを作成することができます。yyaxisで切り替えした後の設定は1軸グラフと同じです。特に色の指定がない場合は、グラフ中の線の色と対応するy軸の色が対応しているとわかりやすいです。（例では第1軸が赤、第2軸が黒）

2軸グラフ
clf;
figure();

yyaxis left %左軸
inputp=plot(ResCell{2,2}.a_1.x,'--r');       %プロット（Lineプロパティで指定する場合）
ylim([0,10]);
ylabel('入力');

yyaxis right  %右軸
resultp=plot(ResCell{3,2}.a_1.y,'-k');       %プロット（Lineプロパティで指定する場合）
ylabel('計算結果');
ylim([0,50]);

ax=gca;
[ax.YAxis.Color]=deal([1,0,0],[0,0,0]); %各軸の色の設定

xlim([1,10]);
xlabel('横軸');
legend([inputp;resultp],{'入力','計算結果'},"Location","northwest","NumColumns",2); %凡例
1-4.jpg

時系列グラフとケース単位のグラフ

時系列グラフもplot関数でグラフにできますが、グラフ編集の拡張性の観点から、横軸は数値でプロットさせた方が柔軟性が高いです。具体的には、TimeTable型変数TTをプロットする場合は

横軸をdatetime型時刻
p=plot(ResCell{3,2}.a_1.TT.Time,ResCell{3,2}.a_1.TT.Var1,'-k');

よりも

横軸をシリアル日付値
p=plot(datenum( ResCell{3,2}.a_1.TT.Time ), ResCell{3,2}.a_1.TT.Var1,'-k');

とした方が、良いということです。以下にdatetime型の時刻（年間）と対応する値Varのグラフを作成する例を示します。なお、目盛は月単位としていますが、月によって日数が異なりますので、カレンダー期間の月数を計算するcalmonths関数を用いています。このままでは横軸がただの数値になりますので、最後にdatetick関数を用いて適切な日付フォーマットを指定し、目盛を維持するように 'keepticks'オプションを指定します。また、ケース間で結果を比較する場合はfor文で数値Var部分のみ変えると良いでしょう 。このあたりがプログラムと結果ファイルの構成をきちんと決めた恩恵ですね。

時系列グラフとケース単位のグラフ
clf;
for iCase=1:nCase　% ケース単位でグラフを作成する場合
   figure();   
   Time=ResCell{3,iCase}.a_1.TT.Time;
   Var =ResCell{3,iCase}.a_1.TT.Var1;　% iCase毎に変化する部分 
   %1.データのプロット 
   p=plot(datenum( Time ), Var,'-k'); %横軸をシリアル日付値 
   ylabel('計算結果');    % 日付軸の範囲と目盛 
   xlim(datenum([Time(1), Time(end)])); 
   xticklabels(datenum( Time(1):calmonths(1):Time(end))); 
   xticks(datenum( Time(1):calmonths(1):Time(end))); 
   datetick('x','mm月','keepticks'); 
   xlabel('日付');
end

「左がConventional、右がProposed」というように、簡単に結果を比較することができます。
1-5-6.jpg

指標の計算と疑似カラープロット

例として、各ケース・各パラメータの結果(y)の平均値をグラフにするとします。指標の計算は、for文を使って全ケース・全パラメータを対象としましたが、まとめ方によってはcellfun関数またはstructfun関数でスマートにできるかもしれません。

指標の計算
% 指標の計算parameter={'a_1','a_2'}; %グラフに使用するパラメータ
Z=zeros(nCase+1,length(parameter)+1);
for X=1:nCase 
  for YYY1:length(parameter) 
       Z(X,Y)=mean(ResCell{3,X}.(string(parameter(Y))).y);   
   end
end

この場合、3Dグラフで書く方法もありますが、ここではpcolor関数を用いて、平均値を色で示す疑似カラープロットでグラフを書きます。ここで紹介するグラフは heatmap関数でも書けますが、最初に例示したような「カラープロットの上に補助線を引く」などの操作の柔軟性はpcolor関数の方が高いと思われます。

疑似カラープロット
clf;
figure();% 疑似カラープロット
s=pcolor(0.5:(nCase+1),0.5:(length(parameter)+1),Z);
xticks([1:nCase]);
xticklabels(ResCell(1,:));
xlabel('Method');
yticks([1:length(parameter)]);
yticklabels(parameter);
ylabel('Parameter value');
1-7.jpg

色の指定・変更はcaxis関数で'manual'、 上下限値を指定することで設定できます。グラフにはcolorbarも付けましょう。

疑似カラープロットの色合いの指定
caxis('manual'); %手動へ変更
caxis([10,40]);  %上下限値
colorbar         %カラーバーの表示
1-8.jpg

グラフの種類

個人的によく使用するグラフは、これらの他にも

  • scatter関数:散布図
  • bar関数: 棒・積み上げ棒グラフ

などがありますが、基本的にはplot関数と同じになりますので、今回は割愛します。希望があれば書きます。

また、「論文に貼るグラフを決めたい」などとりあえずグラフを作りたい、眺めたい場合は、tiledlayoutを用いて複数のグラフを作ると良いかもしれません（詳細はこちら）。

2.共通事項（基本設定）

基本的に論文で同一のサイズ・型に沿ったグラフを作るかと思いますので、共通事項を関数として定義しておくと良いでしょう。以下は、設定の例を示しております。

グラフの共通事項を設定するfigset関数
function figset(Option)
arguments    
Option.figPosition=[0 0 9 6];   %デフォルトFigサイズ指定
 Option.axPosition=[1 1 7.5 4.5];%デフォルトaxサイズ指定
end
fig=gcf; %Figure ハンドル番号の取得
fig.Units='centimeters';  %サイズ指定のために1度 cm単位へ変更
fig.Position=Option.figPosition;%サイズ指定
fig.Units='normalized';   %規格化単位に戻す

ax=gca;  %軸ハンドル番号の取得
ax.Units ='centimeters';       %サイズ指定のために1度 cm単位へ変更
ax.Position = Option.axPosition; %サイズ指定
ax.Units='normalized';         %規格化単位に戻す
%ax.FontName = 'MS 明朝'; %日本語の場合
ax.FontName = 'Times New Roman'; %英語の場合
ax.FontSize = 7; %フォントサイズ
grid on     %目盛り線box on      %グラフの枠
ax.GridColor=[0,0,0]; %グリッドの配色
end

左が変更前、右が変更後のグラフです。
2-1.jpg

グラフ毎に変えたいパラメータは構造体Optionで変更できるように、argumentsに宣言を追加し、この関数の引数で指定するようにしましょう。ここでは、Figサイズと軸のサイズを変えるようにしました。グラフ例2はカラーバーの分だけ狭くしています。各プロパティの詳細はFigure のプロパティ、Axes のプロパティを参照してください。なお、また各プロパティでUnitsを2回設定していますが、これはサイズ指定のためです。通常cmで指定した方がサイズ感がわかりやすいものの、（3.アノテーション・拡大図の追加 含む）File exchange等で公開されている多くの関数が規格化('normalized')サイズをベースとしていますので、エラーがでないように元に戻しています。

3.アノテーション・拡大図の追加

グラフをかっこよく、よりわかりやすくするための工夫ですが、グラフのうちの特定の部分を拡大したり、数値として示したりしたいことが（たまにですが）あります。アノテーションはグラフ領域内に文字や矢印などを挿入するものを示します。

3.1 矢印の追加

annotation関数に'textarrow'を指定し、 x,yの値を[始点,終点]とすることで矢印を引くことができますが、x,yは規格化サイズなので、グラフ軸の値から規格化するように変換する関数sizeconvを用意します。annotation関数のハンドルを取得し、矢印のサイズ変更もできます。

矢印の追加
nsizeValueFrom=sizeconv(8.5,12); %矢印の始点(x,yの値を規格化ベースに変換)
nsizeValueTo=sizeconv(9,16);   %矢印の終点(x,yの値を規格化ベースに変換)
x=[nsizeValueFrom(1,1) nsizeValueTo(1,1)];
y=[nsizeValueFrom(1,2) nsizeValueTo(1,2)];
ta=annotation('textarrow',x,y,'String','y=\lambda*x (\lambda=2)','Interpreter','tex'); %矢印の挿入
ta.HeadLength=8; %矢印のサイズ

矢印は始点(X,Y)=(8.5,12)から終点(X,Y)=(9,16)で書かれています。
3-1.jpg

sizeconv関数は以下のように設定しています。

sizeconv
function normalizedValue=sizeconv(XpositionValue,YpositionValue)
    ax=gca;  %軸ハンドル番号の取得
    normalizedValue(1,1)=ax.Position(1)+(XpositionValue-ax.XLim(1))/ (ax.XLim(2)-ax.XLim(1)) * ax.Position(1,3);
    normalizedValue(1,2)=ax.Position(2)+(YpositionValue-ax.YLim(1))/ (ax.YLim(2)-ax.YLim(1)) * ax.Position(1,4);
end

3.2 グラフ領域中の数値の追加

特筆すべき数値がある場合はannotation関数に'text'関数を指定し、数値を入れるのも有効だと思います。下記は2本の補助線の高さmaxY、minYを示した例です。

グラフ領域中の数値の追加
nsizeValue=sizeconv(X,maxY); %X,maxYの文字開始位置(Xは固定)
num2glf(nsizeValue,string("max="+num2str(maxY,'%3.1f')),"Color",[1,0,0]); %グラフ領域中の数値の追加
nsizeValue=sizeconv(X,minY);  %X,maxYの文字開始位置(Xは固定)
num2glf(nsizeValue,string("min="+num2str(minY,'%3.1f')),"Color",[0,0,1]); %グラフ領域中の数値の追加

グラフに表示する値および位置（高さ）は変数にしていますので、文字の位置も自動的に変更します。
3-2.jpg

num2glf関数は自作した関数であり、引数で指定された位置、文字、オプション（色）に従いannotation関数を設定するようにします。

グラフ領域中に数値を追加するnum2glf関数
function num2glf(normalizedValue,text,Option)
arguments    
   normalizedValue double;
   text(1,1)=string();    
   Option.Color(1,3) double  =[0,0,0];
end

ax=gca;  %軸ハンドル番号の取得
position(1,1:2) =normalizedValue;
position(1,3) =0.2; %テキストボックスの枠のサイズ(横)
position(1,4) =0.1; %テキストボックスの枠のサイズ(縦)
annotation('textbox',...
    position(1,:),...
    'Color',Option.Color,...
    'String',text,... 
   'LineStyle','none',...
    'FitBoxToText','off',...
    'FontName',ax.FontName);
end

3.3 拡大図

拡大図はFile Exchangeで公開されている ZoomPlot が非常に充実していますので、そちらを使うのがおすすめです。現在の最新版 (ZoomPlot v1.2)はマウス操作で拡大図の配置箇所と拡大箇所を指定できますので、非常に便利です。

ZoomPlot
ax=gca; %元のグラフの軸ハンドル番号の取得
zp = Function.ZoomPlot.BaseZoom();
zp.plot();
zp.subAxes.FontName = ax.FontName; %元のグラフと拡大図のフォントの統一

このコードでは、マウス操作の入力待ちになりますので、プログラムが一時停止したようになります。したがって、下記のように拡大図配置領域を設定し、右クリックで確定します。その後、拡大箇所領域を設定・右クリックで確定をすればプログラムが続行します。

ZoomPlot.gif

このような機能を使えば所望のグラフが大体できます。

4.グラフの出力

出力は主に2通りあります。

4.1 グラフ毎にコピー&ペースト（ワードに貼る場合）

ワードに貼る場合はこちらが最善かと思います。この方法も「Figureウィンドウからエクスポートする方法」と「copygraphics関数をする方法」に分かれます。作成したグラフを微調整せずにそのまま貼りたい場合はcopygraphics関数

Figをクリップボードにコピー
copygraphics(fig);

を使い、調整する場合はFigureウィンドウ上で修正すると良いでしょう。

4.2 ファイル出力（LaTeXに貼る場合や別ソフトでグラフを加工する場合）

この記事を閲覧する皆さんはこちらが多い気もしますが、LaTeXに貼る場合は貼りたい場所のファイル名を一致するように設定しておけば自動的に反映されるので、こちらの方が圧倒的に良いでしょう。また、別ソフトでグラフを加工する場合もこちらの方が良いと思います。ファイル出力は exportgraphics関数

グラフのファイル出力
exportgraphics(fig,filepath);

を指定すれば出力されます。

おわりに・配布プログラム

長くなりましたが、これで基本的なグラフはかけると思います。ここで紹介したグラフを作成するプログラム(graph.mlx)およびフォルダ構成をgitにまとめて公開しております。

MATLABを使った卒論・修論・論文にも使えるグラフ作成方法まとめ（補助線・2軸グラフ・疑似カラープロット・アノテーション・拡大図の書き方etc）

なお、こちらで解説していますので、プログラム中のコメントは最小限となっています。ご要望があれば追加していきます。

ZoomPlotは現在のバージョンV1.2を入れたままにしておりますが、不具合があるかもしれません。詳細はオリジナルを参照してください。

また、おすすめのデータ管理方法やグラフ作成がございましたら、ご教授頂ければ幸いです。

関連記事・参考サイト

gitで公開したプログラムに関連する記事

gitで公開しているプログラムの機能に関するリンク（MATLABプログラム勉強中の方はこちらもどうぞ）

41
33
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
41
33

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?