\newcommand{\argmin}{\mathop{\rm argmin}\limits}
\newcommand{\bm}{\boldsymbol}
こんにちは.YutaKです.
今回は普段の機械学習・数理最適化の研究を行っている「線形数理・機械学習モデルに基づく情報の秘匿化(抽象化)」に関する記事を執筆します.(LT回で使い回そう)
線形数理・機械学習モデルに基づく情報の秘匿化は機密データ解析の文脈で用いられます.機密情報・個人情報を隠す処理なんだぜって,わかりやすいように最初に秘匿化と書きましたが,厳密には抽象化のような柔らかい呼び方をすることが多いです.この抽象化の処理を行うことで,データの重要な特徴は残したままに,情報からリスク性を排除することができるため,様々な安全なデータ解析への応用が可能となります.
通常の暗号化・復号のフレームワークとは異なり,抽象化処理では抽象化したデータ(中間表現)は復号せずに解析を行うことも特徴の一つです.
今回はその抽象化で実際にデータが秘匿化されているのかを見ていきたいと思います.その中で,線形手法に基づく抽象化前の元データの推定を試み,抽象化の処理で秘匿化が実現され,元データの個人情報・機密情報を復元できないことを確認します.
実験
コードの実装についてはJupyter Notebookでの動作を想定しています.
ソースコード
関数の定義など
まず,全体で用いる関数などを示します.
import numpy as np
import os
import pickle
from PIL import Image
def unpickle(file):
with open(file, 'rb') as fo:
dict = pickle.load(fo, encoding='bytes')
return dict
def load_cifar10(DATA_ID):
# ファイル読み込み(num: 10000)
if DATA_ID == 1:
file_path = os.path.join(DATA_PATH, 'cifar_10/data_batch_1')
elif DATA_ID == 2:
file_path = os.path.join(DATA_PATH, 'cifar_10/data_batch_2')
elif DATA_ID == 3:
file_path = os.path.join(DATA_PATH, 'cifar_10/data_batch_3')
elif DATA_ID == 4:
file_path = os.path.join(DATA_PATH, 'cifar_10/data_batch_4')
elif DATA_ID == 5:
file_path = os.path.join(DATA_PATH, 'cifar_10/data_batch_5')
file = unpickle(file_path)
# Loading...
dataset = np.array(file[b'data'])
labels = np.array(file[b'labels'])
return dataset, labels
def plot_cifar10_image(data):
# data is shown as `dataset[index]`
# データの再形成(32x32x3)
image = data.reshape(3, 32, 32).transpose(1, 2, 0)
# 画像の表示
plt.imshow(image)
plt.show()
def load_and_transform_image(image_path):
# 画像の読み込み
with Image.open(image_path) as img:
# 画像をNumPy配列に変換
img_array = np.array(img)
# RGBA画像の場合、RGBに変換
if img_array.shape[2] == 4:
img_array = img_array[:, :, :3]
return img_array.transpose(2, 0, 1).reshape(3072)
def cosine_similarity(a, b):
return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))
CIFAR-10データ読み込み
CIFAR-10のデータは次のとおり読み込みます.リポジトリにも含めていますが,
からダウンロードしてもOKです.
# data-path
DATA_PATH = "/src/data/"
# imports
import os
import numpy as np
import matplotlib.pyplot as plt
DATA_ID = 1
dataset, labels = load_cifar10(DATA_ID)
print(f"dataset: {dataset.shape}, labels: {labels.shape}")
PCAによる抽象化関数の作成
主成分分析(PCA)は多次元データを人間が理解しやすい形に変換する手法です.(特に2・3次元化など)
- 512次元(ピクセル比 1/2)
- 256次元(ピクセル比 1/4)
- 128次元(ピクセル比 1/8)
- 64次元(ピクセル比 1/16)
の4種類の主成分分析による次元削減関数を今回は抽象化関数として扱います.
オリジナルのCIFAR-10の画像データ,
\bm{X} \in \mathbb{R}^{10000 \times 3072}
に対して,ここで次のような,標準正規分布に基づく乱数値で生成されたダミーデータ,
\bm{X}^{\mathrm{anc}} \in \mathbb{R}^{r \times 3072}
が存在することを考えます.今回扱う機密データ解析の文脈では一般に$r \gg 3072$(元データの次元数)であるため,今回の実験では元データの次元数の10倍に$r$の値を設定しています.
ダミーデータに対しても同様に主成分分析の関数を適用します.行列$\bm{F}$は主成分分析に該当する関数です.
\tilde{\bm{X}}^{\mathrm{anc}} = \bm{X}^{\mathrm{anc}} \bm{F} \in \mathbb{R}^{r \times \tilde{m}}
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# アンカーデータの生成
anc = np.random.randn(30720, 3072)
# データの標準化
scaler = StandardScaler()
dataset_scaled = scaler.fit_transform(dataset)
anc_scaled = scaler.transform(anc)
# PCAの適用
pca_512 = PCA(n_components=512)
pca_256 = PCA(n_components=256)
pca_128 = PCA(n_components=128)
pca_064 = PCA(n_components=64)
dataset_intermediate_512 = pca_512.fit_transform(dataset_scaled)
dataset_intermediate_256 = pca_256.fit_transform(dataset_scaled)
dataset_intermediate_128 = pca_128.fit_transform(dataset_scaled)
dataset_intermediate_064 = pca_064.fit_transform(dataset_scaled)
anc_intermediate_512 = pca_512.transform(anc_scaled)
anc_intermediate_256 = pca_256.transform(anc_scaled)
anc_intermediate_128 = pca_128.transform(anc_scaled)
anc_intermediate_064 = pca_064.transform(anc_scaled)
元データ推定のための一般化逆行列の作成
$\bm{X}$を推定する際に条件として$\bm{X}$,$\bm{F}$はデータ復元作業時には未知であるとします.その代わり,$\bm{X}^{\mathrm{anc}}$,$\tilde{\bm{X}}^{\mathrm{anc}}$は既知となります.
このようなヒントが存在するのはセキュリティ上の困難性を上げてしまいます.しかし,このデータが存在することによって機密データ解析手法上のメリットが出てくるので,機密データ解析の文脈ではこのような困難性を上げてしまう条件を前提として考える必要が出てきます.
ここで,元データを推定する関数にあたる行列$\bm{G}$は次のように与えられます.
\argmin_{\bm{G}'} \|
\bm{X}^{\mathrm{anc}} - \tilde{\bm{X}}^{\mathrm{anc}} \bm{G}'
\| = \bm{G} \in \mathbb{R}^{\tilde{m} \times 3072}
\Longrightarrow \bm{G} = (\tilde{\bm{X}}^{\mathrm{anc}})^\dagger \bm{X}^{\mathrm{anc}}
\left(
2{\tilde{\bm{X}}^{\mathrm{anc}}}^\top \tilde{\bm{X}}^{\mathrm{anc}}\bm{G} - 2{\tilde{\bm{X}}^{\mathrm{anc}}}^\top \bm{X}^{\mathrm{anc}}=\bm{O},
\bm{G}=({\tilde{\bm{X}}^{\mathrm{anc}}}^\top \tilde{\bm{X}}^{\mathrm{anc}})^{-1} {\tilde{\bm{X}}^{\mathrm{anc}}}^\top \bm{X}^{\mathrm{anc}} = (\tilde{\bm{X}}^{\mathrm{anc}})^\dagger \bm{X}^{\mathrm{anc}}
\right)
from numpy.linalg import pinv
# 一般化逆行列の計算
g_512 = pinv(anc_intermediate_512) @ anc
g_256 = pinv(anc_intermediate_256) @ anc
g_128 = pinv(anc_intermediate_128) @ anc
g_064 = pinv(anc_intermediate_064) @ anc
各次元数設定における元データの推定
元データの推定処理は次の通り行います.行列$\bm{G}$による変換と,標準化の逆処理をかましています.
dataset_collaborative_512 = scaler.inverse_transform(dataset_intermediate_512 @ g_512).astype(int)
dataset_collaborative_256 = scaler.inverse_transform(dataset_intermediate_256 @ g_256).astype(int)
dataset_collaborative_128 = scaler.inverse_transform(dataset_intermediate_128 @ g_128).astype(int)
dataset_collaborative_064 = scaler.inverse_transform(dataset_intermediate_064 @ g_064).astype(int)
このように推定された画像は元画像と比べて次のような状態です.indexは0〜9999枚目のどの画像について確認するかを示すパラメータです.今回は限定的に最初のデータについて添付しています.
index = 0
plot_cifar10_image(dataset[index])
plot_cifar10_image(dataset_collaborative_512[index])
plot_cifar10_image(dataset_collaborative_256[index])
plot_cifar10_image(dataset_collaborative_128[index])
plot_cifar10_image(dataset_collaborative_064[index])
元画像
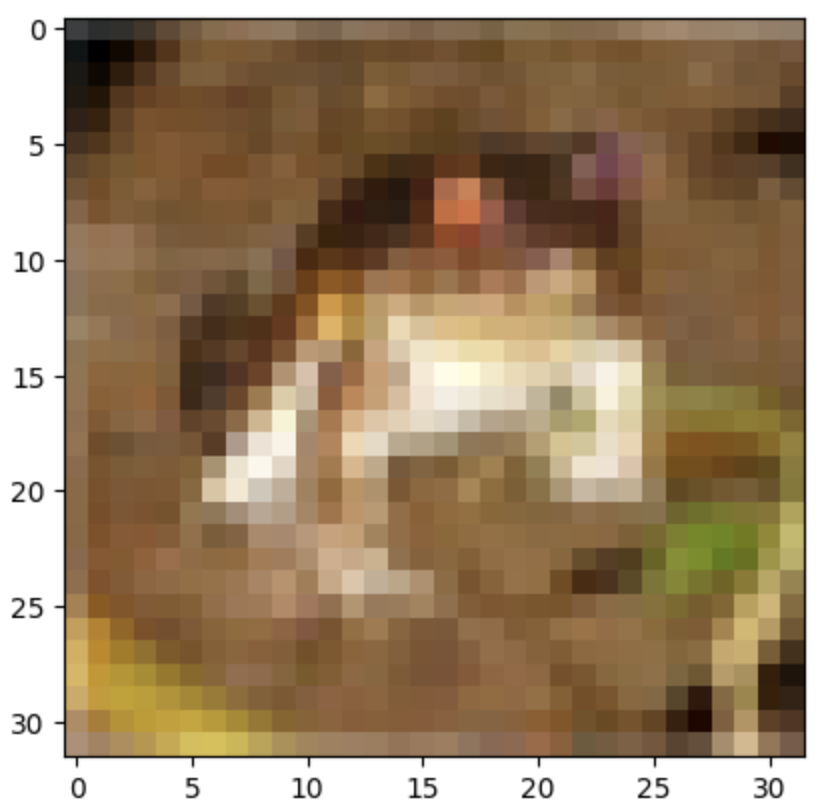
512次元(ピクセル比 1/2)

256次元(ピクセル比 1/4)

128次元(ピクセル比 1/8)

64次元(ピクセル比 1/16)
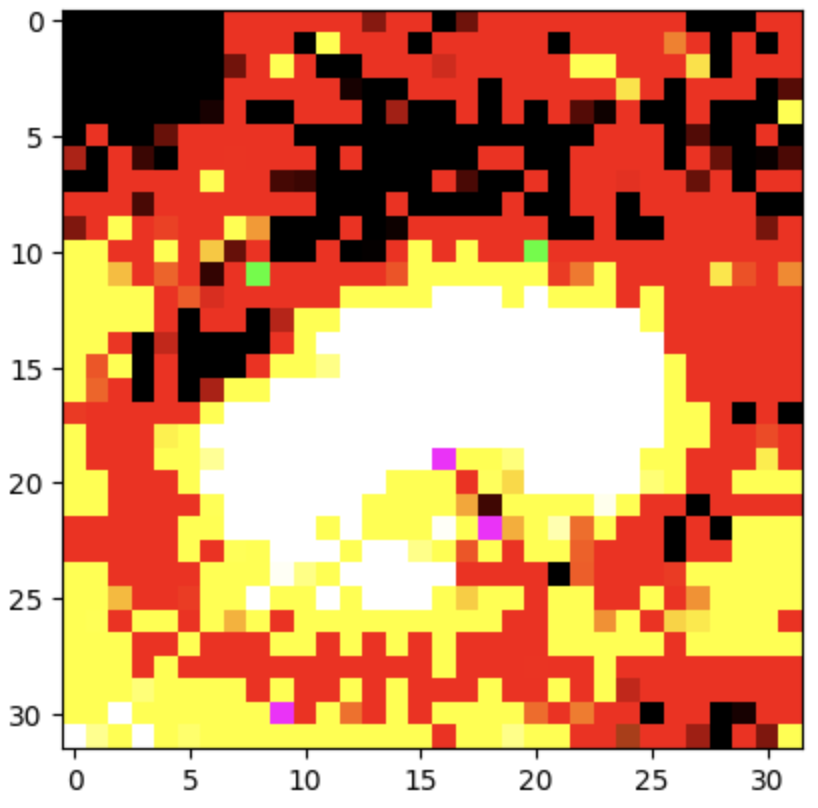
出力に基づく直感的なセキュリティ性の考察
以上のとおり,セキュリティ上の困難性があったとしても,線形数理・機械学習モデルに基づき情報を抽象化・低次元化することで形状以外の情報を画像から省くことができると視覚的に確認できました.この傾向は低次元であればより顕著です.
手法にもよりますが,CIFAR-10の10クラス分類問題ではこのような次元削減によって,次元削減を行なってもある程度の次元数を残していれば,データの解析精度はあまり変化がありません.一見,人間の資格では形状以外認識できない状況ですが,つまり,この画像には人間には見えない形で情報が埋め込まれていることになります.
人間に抽象化・元データ推定・類似度評価を行ってみる
では,人の顔画像などでも同じ傾向が見られるのでしょうか?
残りの部分ではその部分の検証を進めていきます.
512次元と64次元の2パターンを実験します.
今回は1024ピクセル版の 私 と 五条先生 に来てもらいました!
次のコードで私と五条先生を召喚できます.
# 関数の使用例
image_path = '/src/data/五条悟_32.png'
gojo_array = load_and_transform_image(image_path)
gojo_scaled = scaler.transform(gojo_array.reshape(1, -1))[0]
image_path = '/src/data/私_32.png'
watashi_array = load_and_transform_image(image_path)
watashi_scaled = scaler.transform(watashi_array.reshape(1, -1))[0]
plot_cifar10_image(gojo_array)
plot_cifar10_image(watashi_array)
アウトプット


どうみても私と五条先生(学生時代)です.
私と五条先生の元データの類似度
まずは1024ピクセル画像における類似度評価をベースラインとして確認してみましょう.今回は類似度にコサイン類似度を使用します.
「1で似てる,0で関係ない,-1で真逆」という指標になります.
print(
cosine_similarity(
gojo_scaled,
watashi_scaled,
)
)
# output => 0.066
私は 人間であること と カラーグラスをつけていること だけが共通点であるとリカいしました()
私と五条先生の抽象化と元データの推定
まずは構築済みの主成分分析に基づく抽象化関数$\bm{F}$を用いて,私と五条先生の512次元,64次元への抽象化を行います.
# 抽象化
gojo_intermediate_512 = pca_512.transform(gojo_scaled.reshape(1, -1))
gojo_intermediate_064 = pca_064.transform(gojo_scaled.reshape(1, -1))
watashi_intermediate_512 = pca_512.transform(watashi_scaled.reshape(1, -1))
watashi_intermediate_064 = pca_064.transform(watashi_scaled.reshape(1, -1))
次に先ほど学習させた線形モデル(線形関数の行列 $\bm{G}$)を用いて,元画像の推論を行います.
# 元データの推定
gojo_collaborative_512 = scaler.inverse_transform(gojo_intermediate_512 @ g_512).astype(int)
gojo_collaborative_064 = scaler.inverse_transform(gojo_intermediate_064 @ g_064).astype(int)
watashi_collaborative_512 = scaler.inverse_transform(watashi_intermediate_512 @ g_512).astype(int)
watashi_collaborative_064 = scaler.inverse_transform(watashi_intermediate_064 @ g_064).astype(int)
次のコードで出力を行うと,次のアウトプットが得られました.
plot_cifar10_image(gojo_collaborative_512)
plot_cifar10_image(watashi_collaborative_512)
plot_cifar10_image(gojo_collaborative_064)
plot_cifar10_image(watashi_collaborative_064)
アウトプット: 512次元(ピクセル比 1/2)


アウトプット: 64次元(ピクセル比 1/16)

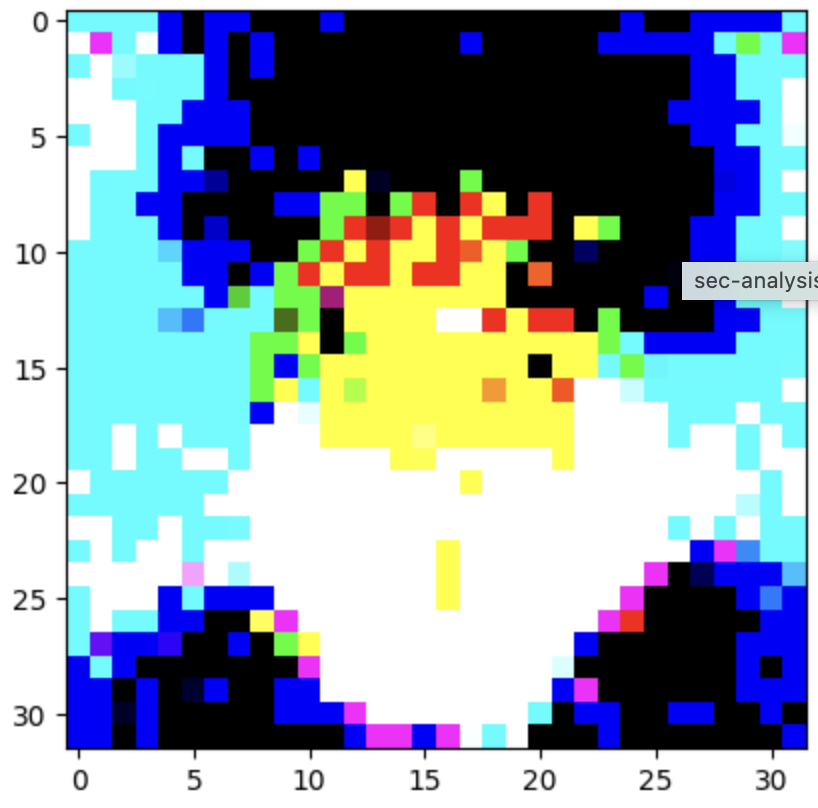
私と五条先生の推定データの類似度
次のコードでコサイン類似度を測定しました.
512次元(ピクセル比 1/2)
print(
cosine_similarity(
gojo_collaborative_512_scaled,
watashi_collaborative_512_scaled,
)
)
# output: 0.035
64次元(ピクセル比 1/16)
print(
cosine_similarity(
gojo_collaborative_064_scaled,
watashi_collaborative_064_scaled,
)
)
# output: 0.004
出力に基づく直感的な考察
私と五条先生の抽象化データの推論結果を見ると,CIFAR-10のデータセットと同様に次元を小さくしすぎると,情報が崩壊しすぎる傾向を確認できました.
ただし,個人が特定される情報を排除しながらも,大まかな特徴が保持されていることも,視覚的には解釈できる結果となりました.
あと,どこかの設定値でミスって俺=五条悟=最強にならないかな?って思ったんですけどちゃんと情報が保持されていたようで,私は五条悟の領域から除外される結果になりました.類似度の傾向は抽象化された情報でも維持されていました.
どうやってこの抽象化関数を解析するの?
(LT回では省略するよ)
今回は抽象化関数による変換前の元データを推定するために行列$\bm{G}$を行いました.しかし,解析を行う上で元データを推定する処理は自明にデータ解析につながるとは言えません.
また,推定処理は機密データ解析のフレームワークを扱う上では,可能性を狭める処理にもなりかねません.
機密データ分析の文脈では,この行列$\bm{G}$をより解析に適した空間への写像に使います.
書いていくと論文が出来上がってしまうので,興味がある方は別途お話ししましょう.
注意書き
線形手法に限った話になります.
抽象化におけるセキュリティ性は非線形ではどうなるんですかね?(論文調査しないと...)
最後に人探し
一緒にお仕事したいという方がいればお声がけいただけると嬉しいです!!!
Kaggleコンペ出場チームメンバーも募集中です!!!(コンピュータリソースは自分持ち,知識・経験よりモチベーション重視)
今晩飲みにいく人も探してます!!!
来年の拠点に福岡が増えそうなので,福岡の友達増やしたいです!!!
連絡待ってます!