Unityの基本的なColliderの形状完全に理解した

TL; DR

箱はなるべく大きさを保とうとする
円・球はとにかく大きいほうが優先される

事の発端

VRアプリでモノを持てる範囲を可視化したく、コライダーの範囲を調べていたら、スケール・回転が絡んだ際にメッシュの見え方と異なる奇妙な動きを見せたので、調査してみました

環境

Unity 2020.3.26f1 Personal for Windows

コライダーの種類

現在、Unity3Dには以下のコライダーが実装されています。

• Terrain Collider
• Mesh Collider
• Sphere Collider
• Box Collider
• Capsule Collider
• Wheel Collider

このうち、本稿で扱うのはWheel Collider以外の5つです。

各コライダーの形状

それでは、各コライダーについてそれぞれ見ていきましょう。
Sphere、Box、Capsuleはそれぞれ最後にコードを載せています。

Terrain Collider

まずはTerrain Colliderですが、なぜこれから始めたかというと、「一番単純だから」です。
Terrainは仕様上、Transformで回転・スケール変更させることができません。(参考1(回転))(参考2(スケール))
すなわち、Terrain Colliderの形状は「同じ場所にオブジェクトを設置し、同じTerrainを描画する」だけで表示できます。
なお、これは「表示」のみであり、「形状をMeshとして取得する」はそれらしき関数が見つかりませんでした。(情報提供求ム)

Mesh Collider

次にMesh Colliderですが、こちらは完全にTransformの影響を完全に受けるため、変な変形をしても見た目通りの位置にコライダーが配置されます。すなわち、同じようにMeshRendererを配置してあげれば問題なく描画できます。


この画像は、Unity標準のPlaneを以下のように配置し、Y軸正→負の向きに(真上から)見たものです。

• 親オブジェクト pos=(0,0,0) rot=(-45,-30,45) scl=(4,3,2)
  • 子オブジェクト pos=(0,0,0) rot=(0,0,0) scl=(2,3,4) ←Plane

このような形状になっても、Mesh Colliderは見た目通りに配置されます。

Mesh Colliderに関して注意点が2つあります。
1つはオブジェクトの配置です。このような変な変形を加えたものをオブジェクトとは別に描画する場合、描画用オブジェクトを配置するために親オブジェクトを最低1個置く必要となってきます。理論上、親が1個あればどんな変形がされていても再現はできるのですが、Matrix4x4を使った高度な計算が必要なので、不安な場合はRootからのTransformを再現しましょう。
もう1つはConvex設定です。Convex(凸多面体)でないメッシュに対してこのチェックを入れるとコライダーが自動で凸多面体に変形され、元のメッシュから形状が変わってしまいます。このようなコライダーの形状を調べる関数はなさそうです(情報求ム)。そのため、このようなオブジェクトを表示したい場合、予めBlenderなどで凸多面体化したメッシュを作っておくのが無難です。

余談ですが、Planeは単純な形状の割には画像のように細かくメッシュを割っていたり、薄いBox Colliderで済ませればよいところをわざわざMesh Colliderを使っていたりで重いので、基本的には使わないようにしましょう。

Sphere Collider

さて、ここからが本題です。RotationやScaleが絡むと難解になるシリーズが3つ続きます。

まずは、玉転がしゲームでおなじみ、Sphereです。
SphereにはCenterとRadiusという2つのパラメータがあり、それぞれ球の中心Cと半径Rを指定できます。(以下、CやRはこのパラメータを表します。) さて、このコライダーの「中心」、どのように計算されているでしょう？

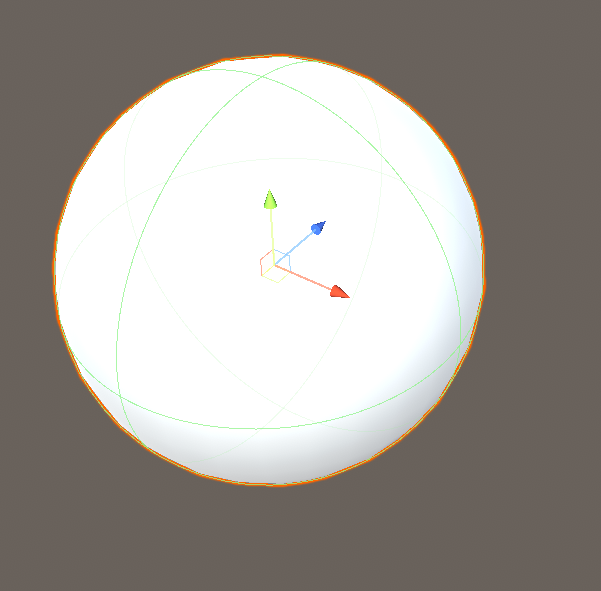
初期値が(0,0,0)であること等から、この数値はオブジェクトのローカル座標を使っています。オブジェクトを回転させればちゃんとそれに合わせて回転します。下の画像で、左の画像はCenterを(0,1.5,0)にしたもの、右の画像はそれをさらに(0,0,90)だけ回転させたものです。なお、この後出てくるSphereの画像は全てRを初期値の0.5としています。

では、左のオブジェクトのScaleを(1,0.5,1)にするとどうなるでしょう？
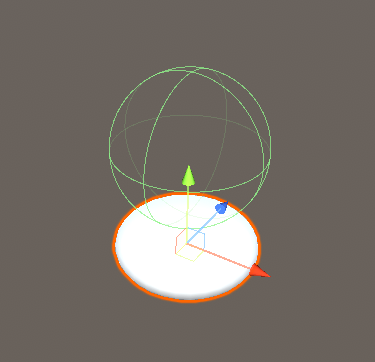
こうなります。メッシュはつぶれるのにコライダーはつぶれていません。また、コライダーの中心が(0,0.75,0)に来ました。

中心が移動するのは納得できますね？Centerで指定する座標はローカル座標なのでY方向の1.5の移動は0.5倍されて0.75になりました。
ちょっと分かりづらくなってしまうので、Cを(0,0,0)に戻して真横から見てみましょう。見づらいのでLightを消し、大きさの比較とするためScaleを(1,1,1)にしたCubeを下に置いておきます。

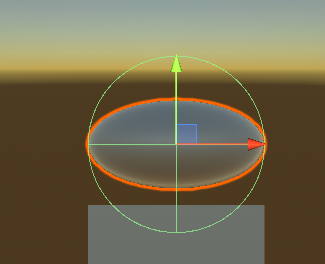
見た目は縦につぶされているのに、コライダーの緑の線は完全な球のままです。

この状態で、Scaleを(0.7,0.5,1.2)とし、さらに変形を加えてみましょう。


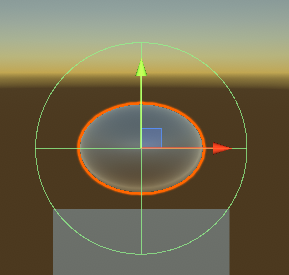
半径が広がりました。

ここで着目すべき点は、「いくら変形してもコライダーは球のまま」であるという点です。Mesh ColliderではScaleを変更すれば同様に引き延ばされたりつぶされたりするので、明らかに挙動が異なります。

ここで、1つの仮説が生まれます。それは「半径は(自身のScaleの3値の最大値)×Rの値で決まる」というものです。実際、この画像でも、半径は(0.7,0.5,1.2の最大値である1.2)×R=0.6となっています。

しかし、この仮説は以下の検証で否定されます。

このSphereを、Scaleが(0.5,0.5,0.5)な空GameObjectの子に置いてみましょう。もちろん、SphereのTransformの値は変更せず。仮説通りであれば、SphereのTransformは変更していないので半径は変化しないはずです。


はい、明らかに小さくなっています。半径がちょうど半分になりました。

すると、次の可能性として「すべての親のScaleを掛け合わせた値の最大値」を考えたくなりますが、その可能性はすぐに消えます。なぜなら、Scaleの同じ成分が同じ方向での伸縮を指すことが保証できないためです。例えば、親オブジェクトで(0,90,0)の回転を行うと子オブジェクトで(1,1,2)の拡大を加える操作は親オブジェクトでは(2,1,1)の拡大と同じことになります。これが90度単位ならよいですが、任意の角度を回転させられるUnityの仕様上、このようなことはうまくいきません。

ではどう考えるか、ということですが、いくらかの実験の結果、次のような説を生み出しました。それは、

(ローカル座標において(R,0,0),(0,R,0),(0,0,R)の3つの点を置いたときに(0,0,0)の点からワールド座標上で最も遠い点との距離)を半径に用いる

というものです。別の説明をすると、

Sphere ColliderのあるオブジェクトAの子に3つのオブジェクトX,Y,Zを置き、それぞれlocalPositionを(R,0,0),（略）としたとき、Aを中心とし、X,Y,Zの3点を内包する最小の球の位置にコライダーが配置される

ともいえます。

Scaleの問題があると言っても、Rootからたどれば位置と回転は必ず計算でき、上記のようなScaleに頼る必要がありません。

幸いなことに、Unityでは「ローカル座標をワールド座標にする」ことが以下のように簡単にできます。

Matrix4x4 calcMat = transform.localToWorldMatrix;
Vector3 worldPosition = calcMat.MultiplyPoint3x4(localPosition));

このlocalPositionにVector3.rightなどを代入すれば、transformの座標系からワールド座標に変換することができます。

Sphere Colliderの形状通りにMesh Rendererを配置するスクリプトの例を置いておきます。

/*
 * 描画用オブジェクトを用意し、MeshFilter(Unity標準のSphere)とMeshRendererをアタッチしておく
 * */
SphereCollider spc; // 範囲を描画したいSphere Collider
Vector3 position; Vector3 scale; // 描画用オブジェクトの位置とスケール
Transform baseTF = spc.transform;
Matrix4x4 calcMat = spc.transform.localToWorldMatrix;
{
    position = calcMat.MultiplyPoint3x4(spc.center);
    scale = Vector3.one * spc.radius * 2 * Mathf.Max(
        (calcMat.MultiplyPoint3x4(Vector3.left)-baseTF.position).magnitude,
        (calcMat.MultiplyPoint3x4(Vector3.up)-baseTF.position).magnitude,
        (calcMat.MultiplyPoint3x4(Vector3.forward)-baseTF.position).magnitude
    );
}

Sphere Colliderは以上です。ここまでぶっ通しで読んでくださっている方はそろそろ頭が疲れている頃かと思うので一度休憩を取りましょう。これと同じような重量のコライダーがあと2つあります。(ただ、Sphere Colliderと似ている点も多いので、ここまでのことを覚えておくと少しは軽量になります)

Box Collider

みんな大好きBox Collider。扱いやすく軽量なので、床・壁・スイッチとあらゆる場所に便利。今日はこれをぐちゃぐちゃにしていきます。
まず基本ですが、Box ColliderにはCenter(C)とSize(S)の設定があり、それぞれx,y,zが設定できます。CenterについてはSphere Colliderと同じくオブジェクトのローカル座標でズレを作ります。
問題はSizeです。これもまた奇妙な動きを見せます。一旦(1,1,1)にして様子を見ましょう。

左図はCubeの親にScale=(1.5,1,1)なオブジェクトを置きCube自身の回転を(0,30,0)にしたもの、右図はそれを真上から見たものです。ハイ、もう崩れました。 もうヤダUnity嫌い

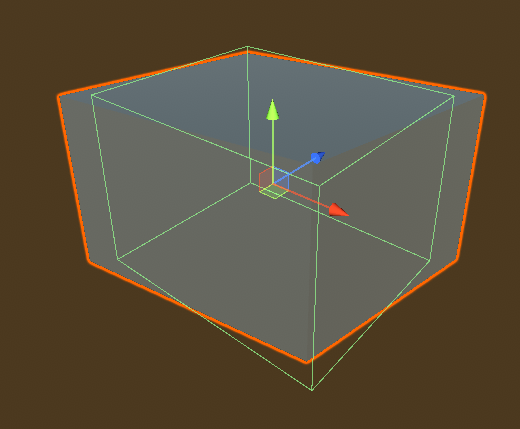
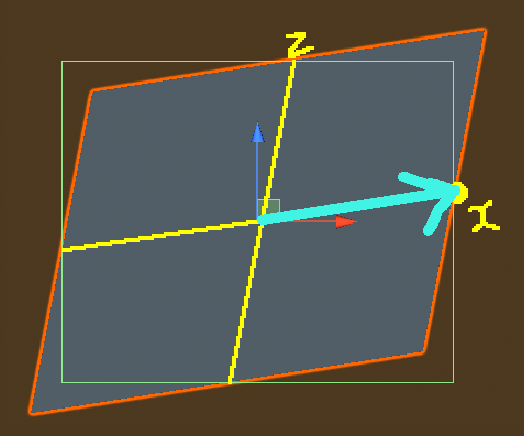
この図を見て、何か取っ掛かりを探しましょう。まず、このコライダーは長方形になっていますが、オブジェクトの「前方」（青の矢印）、「左方」（赤の矢印）と並行な辺があります。このことから、どれだけ変な変形をしていようが、コライダーはオブジェクトのtransform.rotationだけ回転しているようです。
また、上から見たとき、オブジェクトの各辺の中心はコライダーの各辺の中心と同じ場所にあります。また、このような状況においても、Sを変化させると線形的に大きさが変化します。このような状況証拠から、大きさについてこのような説が立ちます。

ローカル座標系で2点O(0,0,0)・P(S.x,0,0)に点を置いたときのワールド座標系における(P→O)ベクトルについて、回転のみ適用したローカル座標系におけるx成分の長さをx方向の大きさとする(y,zについても同様)

なるほどわからん
先ほどの例を使って、一つずつ読み解いていきましょう。ここから先、画面全体を(0,-30,0)だけ回しているので、先ほどの画像とはオブジェクトの向きが少しだけ異なります。

ローカル座標系で2点O(0,0,0)・P(S.x,0,0)に点を置いたとき

この「ローカル座標」は図のようになっています。


図にある黄色の線が"位置における"x軸とz軸、黄色の点がPにあたる点です。なお、赤と青の矢印はBoxColliderのあるオブジェクトの"向きにおける"x軸とz軸を表します。
ここで新たに"位置における"軸と"向きにおける"軸という2つの単語が出てきました。これらは用語ではなく単に説明のために作った語です。"位置における"軸とは、x,y,zのいずれかの数字以外が0となる座標の集合からなる線です。例えば、"x軸"と言うと「y=z=0である点の集まり」を表します。一方、"向きにおける"軸とは、位置とスケールを一切考慮せず、回転をrootから順に自身まで適用していった際の、自身の向きを表します。
通常であればこれらは重なるのですが、図のように歪められた図形ではオブジェクトの向きと座標軸の向きが一致しないことがしばしばあります。

ワールド座標系における(P→O)ベクトルについて

ここは分かりやすいですね。図の水線のようなベクトルです。

回転のみ適用したローカル座標系におけるx成分の長さ

あと一息です。先ほど"位置における"軸と"向きにおける"軸を説明しましたが、今度は"向きにおける"軸を利用します。


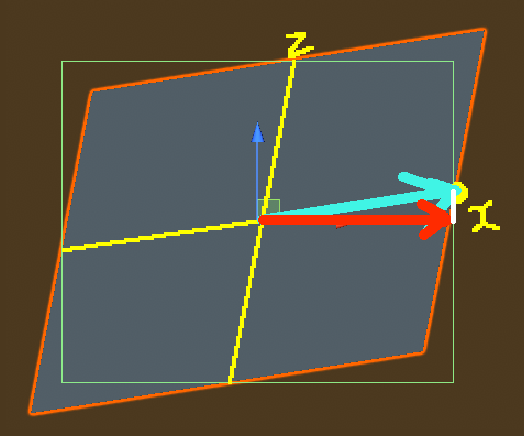
水色のベクトルを"向きにおける"軸に投影し、赤色のベクトルで表しました。Box Colliderはどうやらこの長さぶんの横幅を持っているようです。
ただし、実際のスクリプトでは「投影」は行わず、水色のベクトルを"向きにおける"軸での座標系に変換した上でベクトルのxの値を取るようにしています。

この説を使い、Box Colliderの形状通りにMesh Rendererを配置するスクリプトの例です。このスクリプトではscaleの一部要素が負になることがあるため、負のScaleが支障をきたすスクリプトが付近で動いている場合はMathf.Abs等をかませて下さい。

/*
 * 描画用オブジェクトを用意し、MeshFilter(Unity標準のCube)とMeshRendererをアタッチしておく
 * */
BoxCollider bc; // 範囲を描画したいSphere Collider
Vector3 position; Quaternion rotation; Vector3 scale; // 描画用オブジェクトの位置・回転・スケール
Transform baseTF = spc.transform;
Matrix4x4 calcMat = spc.transform.localToWorldMatrix;
{
    position = calcMat.MultiplyPoint3x4(bc.center);
    rotation = baseTF.rotation;
    scale = new Vector3(
        (Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.left * bc.size.x) - baseTF.position)).x,
        (Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.up * bc.size.y) - baseTF.position)).y,
        (Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.forward * bc.size.z) - baseTF.position)).z
    );
}

疲れましたか？書いている自分も疲れています(
さて、次はこれまでの話の集大成です。

CapsuleCollider

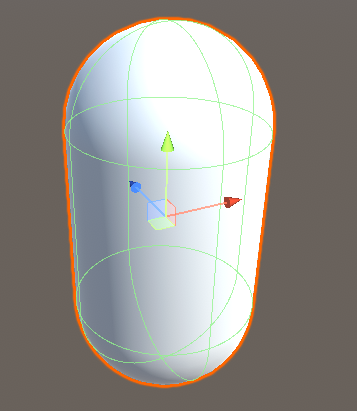
ハイ、本稿のラスボスです。Capsule Colliderの形状に関するパラメータはCenter(C)・Radius(R)・Height(H)・Directionの4つです。このうちDirectionはX-axis,Y-axis,Z-axisの3つから選ぶことになりますが、ひとまずY-axisで説明をします。なお、CはSphereやBoxと同じなので割愛します。
様々な実験の結果、Capsult Colliderは上記で説明したSphereとBoxの合わせ技のようなものと推測できます。コライダーの形状は主に以下の2つのパラメータで説明できます。

• 半径r
• 胴の長さh

図ではこのように表せます。求める順番としてはr→hの順なのでその順に説明します。

半径

半径はSphere Colliderと同じような考え方をします。つまり、rは

自身の"位置に関する"ローカル座標上に3点O(0,0,0),X(R,0,0),Z(0,0,R)を配置し、O→XとO→Zをそれぞれ自身の"回転に関する"ローカル座標に投影したベクトルのうち長いほうの長さ

となります。

胴の高さ

胴の高さについてはBox Colliderと同様に考えます。ただし、(0,H,0)は胴内ではなく球体の部分に乗るため、hは

自身の"位置に関する"ローカル座標上に2点O(0,0,0),Y(0,H,0)を配置し、O→Yを自身の"回転に関する"ローカル座標に投影したベクトルの長さ - R

となります。なお、h<0の場合、hは0とみなされ、半径rの球の形状となります。

このような計算によりrとhを導いたらあとは描画だけなのですが、あいにく胴の長さが可変なカプセル状モデルがUnity公式にはありません。無理やりScaleで変えてしまうと球体の部分が潰れます。そこで、CapsuleColliderはBlendshapeなどで変形できるようように編集しておく必要があります。編集方法は本稿の範囲を外れるため割愛しますが、下記スクリプトで用いるモデルは、Blendshapeを1つだけ作成し、0でh=0、100でh=(r×20)となるようなモデルとなっています。

この説を使い、Capsule Colliderの形状通りにMesh Rendererを配置するスクリプトの例です。axisごとに処理があるため大型スクリプトのように見えてしまいますが、各axisでやっていることは同じです。

/*
 * 描画用オブジェクトを用意し、MeshFilter(セットアップ済みCapsule)とMeshRendererをアタッチしておく
 * */
CapsuleCollider cc; // 範囲を描画したいCapsule Collider
Vector3 position; Quaternion rotation; Vector3 scale; // 描画用オブジェクトの位置・回転・スケール
Transform baseTF = cc.transform;
Matrix4x4 calcMat = cc.transform.localToWorldMatrix;
{
    position = calcMat.MultiplyPoint3x4(cc.center);
    float height; // h
    float radius; // r
    Vector3 objectCenterPoint = cc.transform.position;
    switch (cc.direction)
    {
        case 0: // X-axis
            {
                rotation = Quaternion.Euler(0, 0, 90);
                Vector3 topPoint = calcMat.MultiplyPoint3x4(Vector3.right * cc.height / 2);
                float sqrTopDistanceFromForwardVector = (Vector3.Cross((topPoint - objectCenterPoint), baseTF.rotation * Vector3.right).sqrMagnitude) / (baseTF.rotation * Vector3.right).sqrMagnitude;
                radius = Mathf.Max(
                    Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.forward * cc.radius) - baseTF.position)).z),
                    Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.up * cc.radius) - baseTF.position)).y)
                );
                height = (Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.right * (cc.height / 2)) - baseTF.position)).x) - radius);
                height = Mathf.Max(0, height);
            }
            break;
        case 1: // Y-axis
            {
                rotation = Quaternion.identity;
                Vector3 topPoint = calcMat.MultiplyPoint3x4(Vector3.up * cc.height / 2);
                float sqrTopDistanceFromForwardVector = (Vector3.Cross((topPoint - objectCenterPoint), baseTF.rotation * Vector3.up).sqrMagnitude) / (baseTF.rotation * Vector3.up).sqrMagnitude;
                radius = Mathf.Max(
                    Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.right * cc.radius) - baseTF.position)).x),
                    Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.forward * cc.radius) - baseTF.position)).z)
                );
                height = (Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.up * (cc.height / 2)) - baseTF.position)).y) - radius);
                height = Mathf.Max(0, height);
            }
            break;
        case 2: // Z-axis
            {
                rotation = Quaternion.Euler(90, 0, 0);
                Vector3 topPoint = calcMat.MultiplyPoint3x4(Vector3.forward * cc.height / 2);
                float sqrTopDistanceFromForwardVector = (Vector3.Cross((topPoint - objectCenterPoint), baseTF.rotation * Vector3.forward).sqrMagnitude) / (baseTF.rotation * Vector3.forward).sqrMagnitude;
                radius = Mathf.Max(
                    Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.right * cc.radius) - baseTF.position)).x),
                    Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.up * cc.radius) - baseTF.position)).y)
                );
                height = (Mathf.Abs((Quaternion.Inverse(baseTF.rotation) * (calcMat.MultiplyPoint3x4(Vector3.forward * (cc.height/2)) - baseTF.position)).z) - radius);
                height = Mathf.Max(0, height);
            }
            break;
        default:
            throw new Exception("Unknown direction "+cc.direction);
    }
    scale = Vector3.one * radius * 2;
    ObjectCoverRenderer.sharedMesh = mesh;
    ObjectCoverRenderer.SetBlendShapeWeight(0, Mathf.Clamp(height / radius / 2, 0, 100f));
}

あとがき

オブジェクトは歪ませないことが一番