ライブラリのインポート

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
%matplotlib inline 
from scipy.stats import skew
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

データの読み込み


train = pd.read_csv("train.csv")

外れ値処理

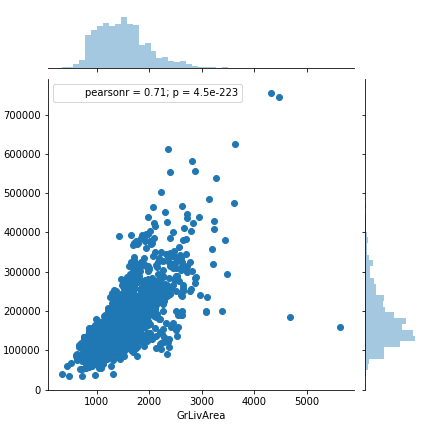
外れ値処理は前回と同様に下図の外れ値とあまりに住宅価格の低いものを処理した。


train = train[~((train['GrLivArea'] > 4000) & (train['SalePrice'] < 300000))]

新たな変数の設計

築年数

前回と同様にこのデータが2011年のものであることから、2011年の時の築年数をあらわす変数を更新した。さらに、改装した場合も改装してからどのくらい経つのかが需要であるので、同様に更新した。


train['YearBuilt'] = 2011 - train['YearBuilt']
train['YearRemodAdd']= 2011- train['YearRemodAdd']

さらに、ひと手間加えようと思う。改装した場合、部屋などは新築と同様にきれいになるので、改装した年を築年数の基準の年に更新してもよいだろう。
よって、築年数に上書きする形で一つ変数でまとめようと思う。

train['YearBuilt'][train['YearBuilt']!=train['YearRemodAdd']]
=train['YearRemodAdd']

面積と質

"TotalSF" は前回と同様に導入した。質（Quality）が高く、面積（SF）が大きければ、住宅価格は高くなると思ったので、新たに、"TotalQual"を'OverallQual'と"TotalSF"の積で表すことにした。また、アメリカでは竜巻が起こることから、地下室が充実していることも大事な要素と考えらるので、地下室も同様のやり方で新たに変数"TotalBsmtSFQual"をつくった。

train["TotalSF"] = train["TotalBsmtSF"] + train["1stFlrSF"] + train["2ndFlrSF"] + train['GarageArea']
train["TotalQual"]=train["TotalSF"] *train['OverallQual']
train["TotalBsmtSFQual"]=train["TotalBsmtSF"] *train['BsmtQual']

欠損値処理

今回、オブジェクト型の変数で扱うのは上でも出てきた'BsmtQual'のみである。
欠損値処理前の状態を見てみよう。

array(['Gd', 'TA', 'Ex', nan, 'Fa'], dtype=object)

nanは0として補い、LabelEncorderで全体を補うことにした。

train = train.fillna(0)
from sklearn.preprocessing import LabelEncoder
for i in range(train.shape[1]):
    if train.iloc[:,i].dtypes == object:
        lbl = LabelEncoder()
        lbl.fit(list(train.iloc[:,i].values))
        train.iloc[:,i] = lbl.transform(list(train.iloc[:,i].values))
train["BsmtQual"].unique()

欠損値処理後はしたのようになった。

array([3, 4, 1, 0, 2], dtype=int64)

対数変換

こちらも前回同様の処理であるので、説明は省く。

train = np.log1p(train)

特徴量の重要度

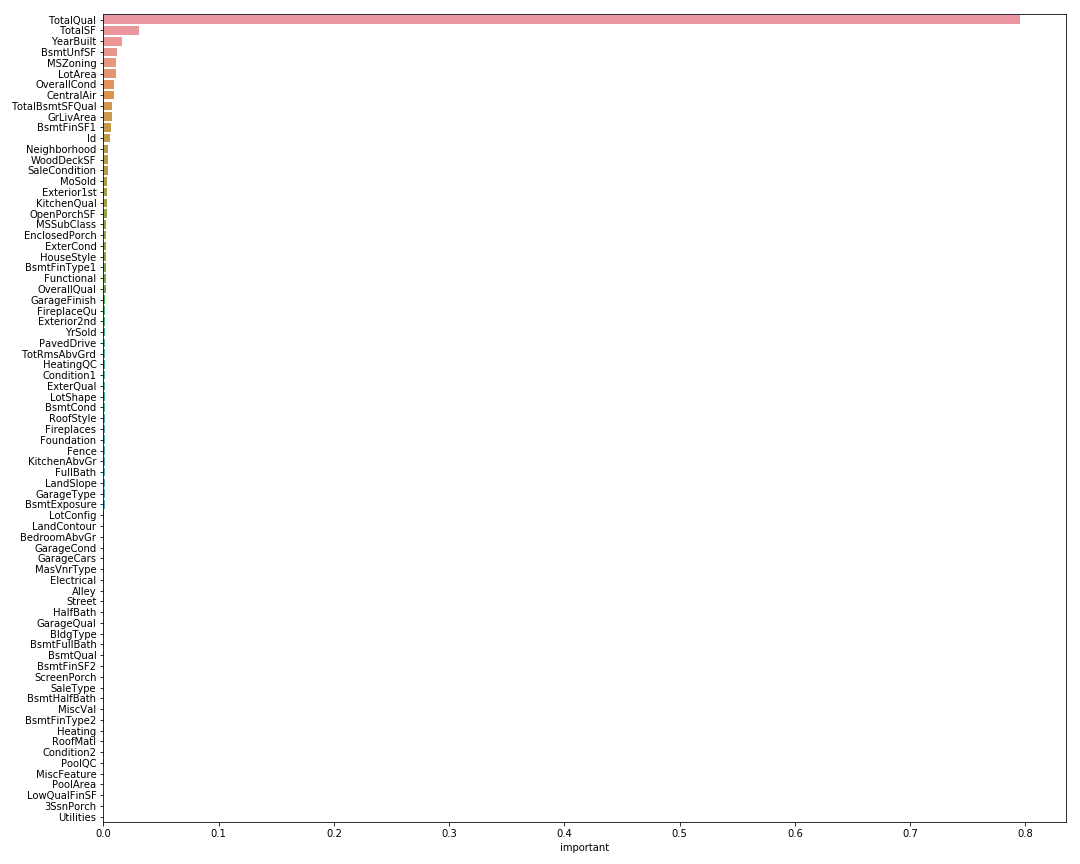
ランダムフォレストを利用して特徴量の重要度を観察してみよう。

新たに設計した変数 "TotalQual" がかなり重要度が高いことが分かる。
今回はこの重要度の高い5つを採用することにした。

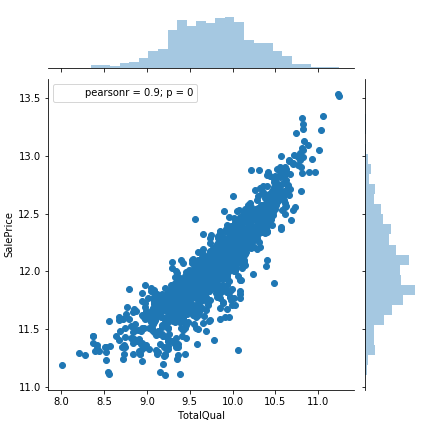
"TotalQual"と"SalePrice"

sns.jointplot("TotalQual","SalePrice",data= train)

かなりSalePriceとつよい関係があることが分かる。自分で作った変数がここまできれいな関係があるとうれしい。

学習

前回と同様にLasso回帰で行った。

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 0)
las = Lasso(alpha=0.001)
las.fit(X_train, y_train)
print("ラッソ回帰でのRMSE：",np.sqrt(mean_squared_error(las.predict(X_test), y_test)))

ラッソ回帰でのRMSE： 0.14472654344982308

考察

前回より結果は悪かったが、変数を絞り、自分で新たな変数を作ることでデータ分析の難しさと楽しさを感じれた。前回に加えてということもありだいぶ省いたため、26日までに修正を加えたい。

Kaggle House Prices