PRML 演習問題 5.23（標準） 解答

問題

２層ネットワークの正確なヘッセ行列に関する 5.4.5 節の結果を、入力から出力へ直接つながる、層を飛び越えた結合を含むように拡張せよ。

本文に書いてあったこと

層を飛び越えた結合がない場合、ヘッセ行列の各要素は

\delta_k = \frac{\partial E_n}{\partial a_k}, 
\ \ \ \ \ 
M_{kk'} = \frac{\partial^2 E_n}{\partial a_k \partial a_{k'}}
\tag{5.92}

を用いて以下のように書ける。

１. 両方の重みが第２層にある：

\frac
{\partial^2 E_n}
{\partial w_{kj}^{(2)} \partial w_{k' j'}^{(2)} }
= z_j z_{j'} M_{kk'}
\tag{5.93}

２. 両方の重みが第１層にある：

\frac
{\partial^2 E_n}
{\partial w_{ji}^{(1)} \partial w_{j' i'}^{(1)} }
= 
x_i x_{i'} h''(a_{j'}) I_{jj'}
\sum_k w_{kj'}^{(2)} \delta_k +
x_i x_{i'} h'(a_{j}) h'(a_{j'}) 
\sum_k \sum_{k'} w_{kj}^{(2)} w_{k'j'}^{(2)} M_{kk'}
\tag{5.94}

３. 重みは１つの層に１つずつある：

\frac
{\partial^2 E_n}
{\partial w_{ji}^{(1)} \partial w_{j' k}^{(2)} }
= 
x_i h'(a_j)
\left\{
\delta_k I_{jj'} + 
z_{j'} \sum_{k'} w_{k'j}^{(2)} M_{kk'}
\right\}
\tag{5.95}

方針

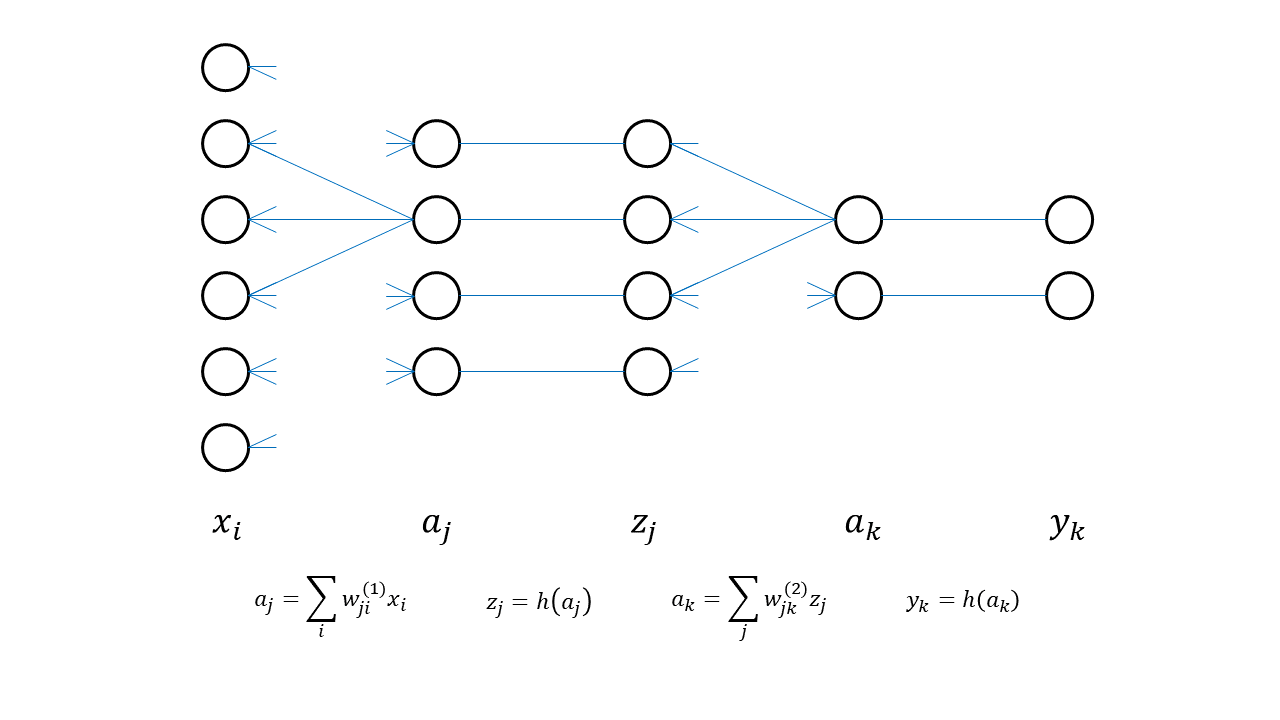
下に本文、および演習5.22で扱ったモデルを図示した。

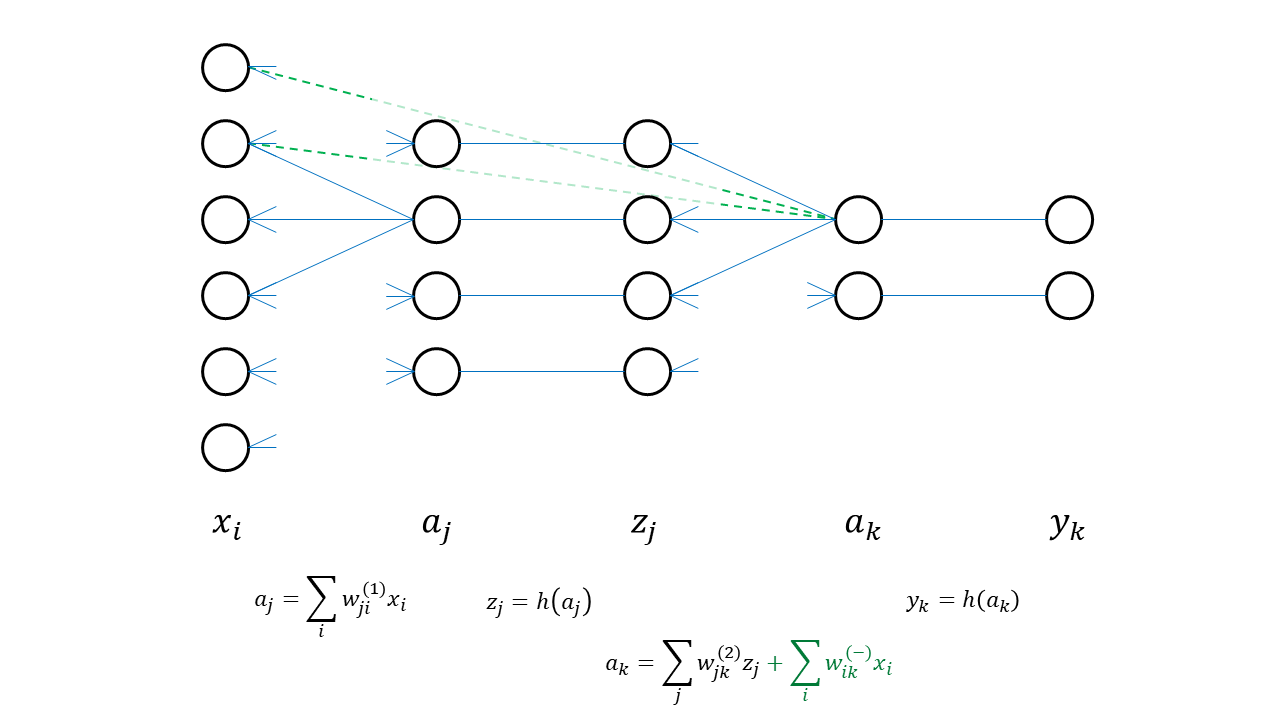
一方、この演習問題で扱う「入力から出力へ直接つながる、層を飛び越えた結合を含む」モデルはこのように表されると考えられる。

層を飛び越えた結合がない場合、第１層と第２層のそれぞれに対応する２種類のパラメータが存在したため、２回微分はそれらの組み合わせである３種類を考える必要あった。しかしこの問題の場合、層を飛び越すためのパラメータが加わるため、２回微分はそれらの組み合わせである６種類に増える。

しかし実際に計算すると、重複する３種類は層を飛び越えた結合がない場合と等しくなることが分かる。

解答

命題１

両方の重みが第２層にあるときのヘッセ行列の要素

\frac
{\partial^2 E_n}
{\partial w_{kj}^{(2)} \partial w_{k' j'}^{(2)} }

は式 $(5.93)$ で与えられる。

証明　$\partial / \partial w_{kj}^{(2)}$ を $\partial / \partial a_k$ で表すと以下のようになる。

\frac{\partial}{\partial w_{kj}^{(2)}}

= \frac{\partial a_k}{\partial w_{kj}^{(2)}}
\frac{\partial}{\partial a_k} 

= z_j \frac{\partial}{\partial a_k}
\tag{ex5.23.1}

これは層を飛び越えた結合がない場合と等しい。（証明終）

命題２

両方の重みが第１層にあるときのヘッセ行列の要素

\frac
{\partial^2 E_n}
{\partial w_{ji}^{(1)} \partial w_{j' i'}^{(1)} }

は式 $(5.94)$ で与えられる。

証明　$\partial / \partial w_{ji}^{(1)}$ を $\partial / \partial a_k$ で表すと以下のようになる。

\begin{align}
\frac{\partial}{\partial w_{ji}^{(1)}}

&= \frac{\partial a_j}{\partial w_{ji}^{(1)}}
\frac{\partial z_j}{\partial a_j}
\sum_k \left\{
\frac{\partial a_k}{\partial z_j}
\frac{\partial}{\partial a_k} 
\right\}
\\

&= \frac{\partial a_j}{\partial w_{ji}^{(1)}}
\frac{\partial z_j}{\partial a_j}
\sum_k \left\{
\frac{\partial}{\partial z_j}
\left(
\sum_{j'} w_{j'k}^{(2)} z_{j'} + \sum_{i'} w_{i'k}^{(-)} x_{i'}
\right)
\frac{\partial}{\partial a_k} 
\right\}
\\

&= \frac{\partial a_j}{\partial w_{ji}^{(1)}}
\frac{\partial z_j}{\partial a_j}
\sum_k \left\{
\frac{\partial}{\partial z_j}
\left(
\sum_{j'} w_{j'k}^{(2)} z_{j'}
\right)
\frac{\partial}{\partial a_k} 
\right\}\\

&= x_i h'(a_j)
\sum_k \left\{
w_{j'k}^{(2)}
\frac{\partial}{\partial a_k} 
\right\}
\tag{ex5.23.2}
\end{align}

これは層を飛び越えた結合がない場合と等しい。また、$j=j'$ の際の２回微分の計算に現れる $\partial h'(a_j) / \partial w_{ji}^{(1)}$ も

\frac{\partial}{\partial w_{ji}^{(1)}} h'(a_j)
= \frac{\partial a_j}{\partial w_{ji}^{(1)}}
\frac{\partial}{\partial a_j} h'(a_j)
= x_i h''(a_j)
\tag{ex5.23.3}

で与えられ、これは層を飛び越えた結合がない場合と等しい。（証明終）

命題３

重みが１つの層に１つずつあるときのヘッセ行列の要素

\frac
{\partial^2 E_n}
{\partial w_{ji}^{(1)} \partial w_{j' k}^{(2)} }

は式 $(5.95)$ で与えられる。

証明　命題１と命題２の証明内容から、$\partial / \partial w_{ji}^{(1)}, \partial / \partial w_{kj}^{(2)}$ は層を飛び越えた結合がない場合と等しいことが示されている。また、$j=j'$ の際の２回微分に現れる $\partial z_j / \partial w_{ji}^{(1)}$ も

\frac{\partial z_j}{\partial w_{ji}^{(1)}}

= \frac{\partial a_j}{\partial w_{ji}^{(1)}}
\frac{\partial z_j}{\partial a_j}

= x_i h'(a_j)
\tag{ex5.23.4}

で与えられ、これは層を飛び越えた結合がない場合と等しい。（証明終）

命題４

両方の重みが層を飛び超えた結合のものであるときのヘッセ行列の要素は

\frac{\partial^2 E_n}{\partial w_{ik}^{(-)} \partial w_{i' k'}^{(-)} }
= x_i x_{i'} M_{kk'} \tag{ex5.23.5}

である。

証明　１階微分は以下のようになる。

\frac{\partial E_n}{\partial w_{ik}^{(-)}}

= \frac{\partial a_k}{\partial w_{ik}^{(-)}}
\frac{\partial E_n}{\partial a_k}

= x_i \frac{\partial E_n}{\partial a_k}
\tag{ex5.23.6}

これは、第２層の重みによる１回微分

\frac{\partial E_n}{\partial w_{jk}^{(2)}}
= z_j \frac{\partial E_n}{\partial a_k}
\tag{ex5.23.7}

の $z_j$ を $x_i$ で置き換えたものである。従って、求める値も式 $(5.93)$ の $z_j$ を $x_i$ で置き換えた式 $({\rm ex} 5.23.5)$ になる。（証明終）

命題５

片方の重みが第２層にあり、もう片方の重みが層を飛び超えた結合のものであるときのヘッセ行列の要素は

\frac
{\partial^2 E_n}
{\partial w_{ik}^{(-)} \partial w_{j k'}^{(2)} }
= x_i z_j M_{kk'}
\tag{ex5.23.8}

である。

証明　

\begin{align}
\frac{\partial^2 E_n}
{\partial w_{ik}^{(-)} \partial w_{j k'}^{(2)} }

&= z_j \frac{\partial}{\partial w_{ik}^{(-)}}
\frac{\partial E_n}{\partial a_k'} \\

&= z_j \frac{\partial a_k}{\partial w_{ik}^{(-)}} 
\frac{\partial}{\partial a_k} 
\frac{\partial E_n}{\partial a_k'} \\

&= z_j x_i M_{kk'}
\end{align}
\tag{ex5.23.9}

より、示された。（証明終）

命題６

片方の重みが第１層にあり、もう片方の重みが層を飛び超えた結合のものであるときのヘッセ行列の要素は

\frac
{\partial^2 E_n}
{\partial w_{ik}^{(-)} \partial w_{ji'}^{(1)} }
=
x_i x_{i'} w_{kj}^{(2)} h'(a_j) M_{kk}
\tag{ex5.23.10}

である。

証明

\begin{align}
\frac
{\partial^2 E_n}
{\partial w_{ik}^{(-)} \partial w_{ji'}^{(1)} }

&= \frac{\partial}{\partial w_{ik}^{(-)}}
\left[
x_{i'} h'(a_j) \sum_{k'}
\left\{
w_{k'j}^{(2)} \frac{\partial E_n}{\partial a_{k'}}
\right\}
\right] \\

&= x_{i'} h'(a_j)
w_{kj}^{(2)}
\frac{\partial}{\partial w_{ik}^{(-)}}
\frac{\partial E_n}{\partial a_{k}} \\

&= x_{i'} h'(a_j)
w_{kj}^{(2)}
\frac{\partial a_k}{\partial w_{ik}^{(-)}}
\frac{\partial}{\partial a_k}
\frac{\partial E_n}{\partial a_{k}} \\

&= x_{i'} h'(a_j)
w_{kj}^{(2)} x_i M_{kk}
\tag{ex5.23.11}
\end{align}

より、示された。（証明終）