■初めに
ベイズ統計に関して学んだことをpythonのコード付きで解説しています(大した実装ではないですが)。
実際に動かしてみたい場合にはnotebookを下記のGitHubレポジトリにアップしていますので、クローンしてお使いください。
https://github.com/YusukeOhnishi/BayesianStatistics
■ベイズ推定の考え方
ベイズ推定では結果から原因を推定するという考え方を行います。
これを具体的に見ていくために袋に入った球を例として考えていきます。下記のような状況を与えます。
・袋A:白色の球3つ、黒色の球7つが入っている。
・袋B:白色の球6つ、黒色の球4つが入っている。
このとき、まず袋を選び球をランダムに引くという問題を考えると、これは数式的には条件付き確率で与えられます。
p(Y|X) \\
Y:袋の選択 \\
Y:球の選択
これは袋に関しての情報(X)が確定したうえで球に関しての情報(Y)を確率で得ようとしています。
X,Yを具体的に与えた場合、下記のようになることがわかると思います。
p(Y=白色の球|X=Aの袋)=\frac{3}{10}\\
p(Y=黒色の球|X=Aの袋)=\frac{7}{10}\\
p(Y=白色の球|X=Bの袋)=\frac{3}{5}\\
p(Y=白色の球|X=Bの袋)=\frac{2}{5}
当然ではありますが、どちらの袋を選ぶのかによって、白または黒色の球を引く確率は変化し、この意味で条件付き確率は袋と球の相関情報を含んでいるということがわかります。
次に、もし仮に選んだ袋がわからないが、その袋から選ばれた球が何色なのかは与えられているという問題設定を考えます。この状況下で例えば、袋から5回球を引き、黒色の球が4回、白色の球が1回出たとします。このとき直感的に考えると、袋Bに比べて袋Aの方が黒色の球が出やすいのでおそらく袋Aから球を引いているということが推察できます。
このように結果(球の色)が与えられた上で原因(袋)を推定するのがベイズ推定の基本的な考え方になります。
■ベイズの定理
上記のような事象を抽象化して、原因をX、結果をYと書くことにします。このとき原因についても確率を考えられるとき(例えば上記の例では2分の1の確率で袋Aを選び、2分の1の確率で袋Bを選ぶなど)、同時分布p(X,Y)を考えることができます。この同時確率は以下の2通りの方法で記述することができます。
p(X,Y)=p(X|Y)p(Y)\\
p(X,Y)=p(Y|X)p(X)
この2式の左辺が同じなので代入しすることで、下記のような式を与えることができます。
p(X|Y)=\frac{p(Y|X)p(X)}{p(Y)}
これをベイズの定理呼びます。この式は上記の例にて問題として設定した、結果(Y)がわかっている場合に原因(X)についての確率を与える式となっています。ベイズ統計においてはこれらの各式に対して名前がついており、それぞれ下記のようになります。
| 項 | 名前 | 意味 |
|---|---|---|
| p(X|Y) | 事後確率 | 結果が与えられた状態での原因の条件付き確率 |
| p(Y|X) | 尤度関数 | 原因と結果を紐づける |
| p(X) | 事前分布 | 原因についての事前知識の確率分布 |
| p(Y) | エビデンス | 事後分布の規格化定数 |
従来の統計学では原因が決まった後に結果を求めるということを行っています。そもそも原因(X)は確率変数ではなく定数だと考えているため、確率分布は存在しません。また信頼区間というものを用いて、その区間に収まっているかいないかで、真偽の推定を行っています。
それに対してベイズ統計学では、原因を確率変数だと捉えて確率分布を求めます。また、ベイズ統計においても信頼区間というものがあり、原因(X)が特定区間に含まれる確率という形で表現します。
■ベイズ統計の流れ
ベイズ統計の流れとしては下記の3つの段階を踏みます。
1.問題の背景を調べ、原因と結果の関係の仮説を立てる。(下調べ)
2.1の情報に基づいて、統計モデルを作成する。(統計モデルの作成)
3.得られたデータから事後分布を推定する。(事後分布の取得)
これらを1つずつ例を交えて見ていきます。
▶下調べ
下調べは次の統計分布作成に際して、事前分布はどうするか、原因の確率分布として何を持ってくるのかということを決めるために行います。
例えば、上記の袋の例であれば、「袋Aの方が少し大きいから袋Bより選ばれやすそうだ。」ということや「各袋に何個ずつ白黒の球がそれぞれ入っているのか。」(今回の場合は上記で示したp(Y|X)の全パターンの値がこれに対応)ということを調査します。
▶統計モデルの作成
ここでは、まず尤度関数を決めます。今回の例の場合ですと、既にp(Y|X)は下調べの段階で完全に求まっています。実際の場合はこれが求まっていることは稀なので、確率分布を仮定して、これを尤度関数として決定します。
次に事前確率を決めます。今回の例ですと、Aの方が選ばれやすいので下記のように下記のように設定します。
p(X=Aの袋)=0.6\\
p(X=Bの袋)=0.4
▶事後分布の取得
事後分布をベイズの定理に従って計算を行います。今回の場合ですと、値が確定しているため手計算にて求めることができますが、通常はマルコフ連鎖モンテカルロ法(MCMC)等を用いて計算を行います。
手計算を行う際にはベイズの定理右辺の分子のみを計算します。分母に関しても計算を行っても良いですが、これは結果が確定した状況においては定数であり、また、確率としての辻褄を合わせる項(確率を全部足すと1になるという性質に合わせる)のため、計算を行う必要はありません。そのため分子計算後に規格化されるように値を決めてしまいます。
例として、袋が選ばれた後に球を3回引いたところ白、黒、白の球が出たとします。このとき求めたい事後確率は下記のように変形できます。
p(X|Y=白、黒、白)\propto p(Y=白、黒、白|X)p(X)=p(Y=白|X)\times p(Y=黒|X)\times p(Y=白|X)p(X)
これを用いることで下記のように事後確率は計算されます。
p(X=Aの袋|Y=白、黒、白)\propto p(Y=白|X=Aの袋)\times p(Y=黒|X=Aの袋)\times p(Y=白|X=Aの袋)p(X=Aの袋)=\frac{3}{10}\times \frac{7}{10}\times \frac{3}{10}\times 0.6=0.0378
p(X=Bの袋|Y=白、黒、白)\propto p(Y=白|X=Bの袋)\times p(Y=黒|X=Bの袋)\times p(Y=白|X=Bの袋)p(X=Bの袋)=\frac{3}{5}\times \frac{2}{5}\times \frac{3}{5}\times 0.4=0.0576
これらを規格化するには
(0.0378+0.0576)/1=0.0954
で割れば良いので、
p(X=Aの袋|Y=白、黒、白)=0.0378/0.0954=0.39622... \\
p(X=Bの袋|Y=白、黒、白)=0.0576/0.0954=0.60377...
このようにして結果が得られます。この結果は、3回袋から球を引いて白、黒、白が出た場合に、自分が引いていたのがAの袋である確率は39.6%、Bの袋である確率は60.4%であるということを意味します。
前節「ベイズ統計の流れ」の「事後分布の取得」で見たようにベイズの定理を用いて、事後確率は計算されていました。前節の場合は3つのデータの場合を扱いましたが、今回はデータ数を4,5,・・・と増やした場合を考えます。またこれをPythonを用いて計算していきたいと思います。
このときベルヌーイ分布というものを考えると便利なので、これを導入します。ベルヌーイ分布Bは下記のように書くことができます。
B(y|\theta)=\theta^y(1-\theta)^{1-y}
この分布は2者択一の問題を扱う際に便利な分布です。このyは今回の場合は0を黒色のに1を白色に対応させます。このときΘの値はy=1に対応した色の出る確率を入れます。例えば袋aを選んだ場合には下記のようになります。
B(0,0.3)=0.7\\
B(1,0.3)=0.3
これを用いて実装を行います。まずは必要なライブラリをインポートします。
#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
%matplotlib inline
#グラフの見た目変更
plt.style.use("ggplot")
次にパラメータを設定します。
#Aの袋を選んだ場合に白球を選ぶ確率
p_a=3/10
#Bの袋を選んだ場合に白玉を選ぶ確率
p_b=3/5
#事前分布(Aの袋を選ぶ確率)
p_prior=0.6
#0:黒の球、1:白の球として引いた球の配列を準備
data=[1,0,1,1,1,0,1,0,0,0,1,1,1,0,1,0,0,1,1,0]
#何回目まで引くのかを指定
N_data=10
dataの配列適当に0か1を入れた配列を用意しています。またN_dataによって球を引く回数を指定しており、この場合10を格納しているので、dataの1番目から10番目までのデータを用いて、10回引いたことを表現します。
次に尤度関数を設定します。
#aの袋に対しての尤度関数
likehood_a=bernoulli.pmf(data[:N_data],p_a)
#bの袋に対しての尤度関数
likehood_b=bernoulli.pmf(data[:N_data],p_b)
このlikehood_a及びlikehood_bにはそれぞれ、下記のような値が入力されており、i番目の要素にはi回目の結果に応じた確率が入力されています。そのため、この配列の各要素の積をとることで尤度関数の値を求めることができます。
likehood_a [0.3 0.7 0.3 0.3 0.3 0.7 0.3 0.7 0.7 0.7]
likehood_b [0.6 0.4 0.6 0.6 0.6 0.4 0.6 0.4 0.4 0.4]
これらを用いて事後確率の計算を行います。
#事後分布に事前分布を代入
pa_posterior=p_prior
pb_posterior=p_prior
#事後分布を尤度関数で更新
pa_posterior*=np.prod(likehood_a)
pb_posterior*=np.prod(likehood_b)
#規格化因子を求める
norm=pa_posterior+pb_posterior
#事後分布を規格化
pa_posterior/=norm
pb_posterior/=norm
#結果の表示
print('Aの袋の確率:',pa_posterior)
print('Bの袋の確率:',pb_posterior)
この結果下記のような出力が得られます。
Aの袋の確率: 0.33902168431669183
Bの袋の確率: 0.6609783156833081
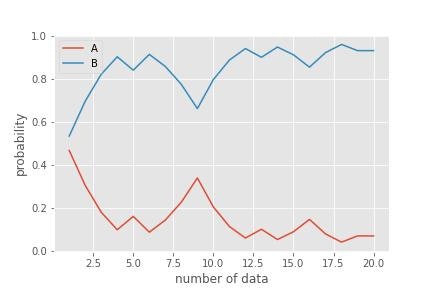
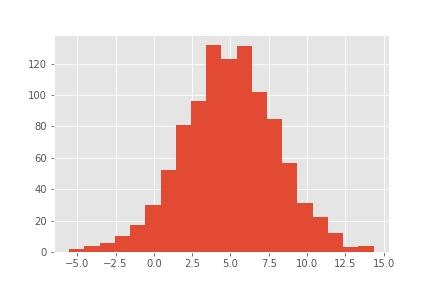
これは先ほど手計算にてデータ数が3の場合に実行したものとは異なっているということがわかります。データ数(N_data)1~20のそれぞれに対して同様に事後確率を計算した結果は下記のようになります。
この結果を見ると、データ数に応じて確率が徐々に変動していることがわかります。これはベイズ統計の大きな性質の一つで、初期で与えた事前確率がデータを与える度に変動していきます。これをベイズ更新と呼びます。
このようにベイズ統計では主観的に与えた事前確率(今回の場合は袋Aの方が大きいからおそらく選びやすいという判断の元60%を与えていた)データを与えること(ベイズ更新)で客観的な確率分布へ収束をさせていくというような動きをします。
■確率分布
上記の「ベイズ更新」においてはベルヌーイ分布にを用いましたがこれ以外にも、確率分布は様々あり、状況に応じて使い分ける必要があります。以下ではいくつかを取り上げて見ていきます。
▶ベルヌーイ分布
改めてベルヌーイ提示しておきます。これは2者択一の問題を扱う場合に用います。
ベルヌーイ分布の分布関数Bは下記のようになります。
B(x|\theta)=\theta^x(1-\theta)^{1-x}
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=\theta\\
V[X]=\theta(1-\theta)
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import bernoulli
▶二項分布
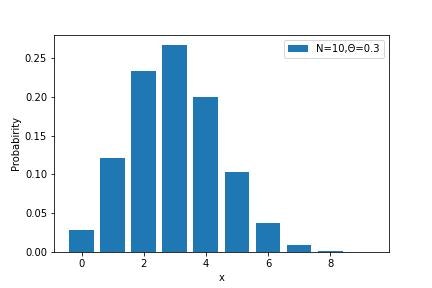
ベルヌーイ分布で与えられるような2者択一の問題を複数回実行した場合には二項分布という分布を用います。例えば、上記の例だとN回袋から引いた場合の黒の出る回数はどの程度かを与えるような確率分布になります。
試行回数をNとして、そのうちx回、Θで確率が与えられる事象が発生した場合の二項分布の分布関数Biは下記のように与えられます。
Bi(x|N,\theta)=\frac{N!}{x!(N-x)!}\theta^x(1-\theta)^{N-\theta}
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=N\theta\\
V[X]=N\theta(1-\theta)
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import binom
▶一様分布
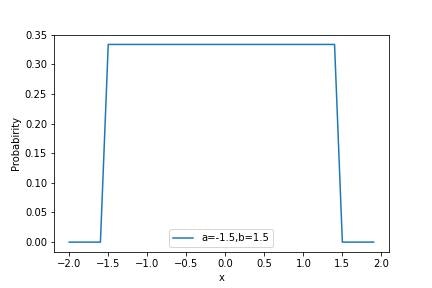
一様分布は事前分布や確率変数に特徴がいない場合に使用される分布で、全ての確率が均等になるような分布です。
あるa~b(b>a)の間の数字xが一様分布に従って生成されるとした場合、一様分布の分布関数Uniは以下のように与えられます。
Uni(x|a,b)=\frac{1}{b-a}
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=\frac{a+b}{2}\\
V[X]=\frac{(b-a)^2}{12}
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import uniform
▶ベータ分布
ベータ分布は確率変数が[0,1]の区間で定義されているような場合に用います。
ベータ分布の分布関数βは下記のように与えられます。
\beta(x|\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1\mathrm{d}t [t^{\alpha-1}(1-t)^{\beta-1}]}
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=\frac{\alpha}{\alpha+\beta}\\
V[X]=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import beta
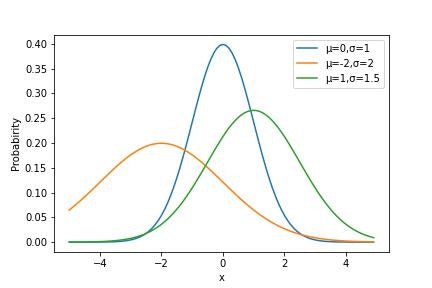
▶正規分布
正規分布は測定誤差など様々な箇所で用います。
正規分布の分布関数Nは下記のように与えられます。
N(x|\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\right)
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=\mu\\
V[X]=\sigma^2
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import norm
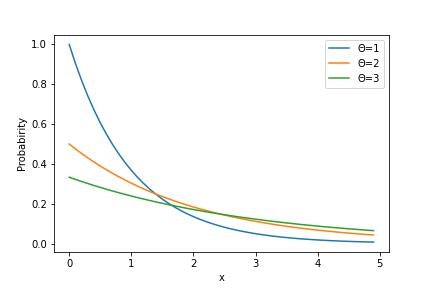
▶指数分布
指数分布は、機械の耐用年数・自身の起こる感覚などを表す際に用います。
指数分布の分布関数Exは下記のように与えられます。
Ex(x|\theta)=\frac{1}{\theta}\exp\left(-\frac{x}{\theta}\right)
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=\theta\\
V[X]=\theta^2
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import expon
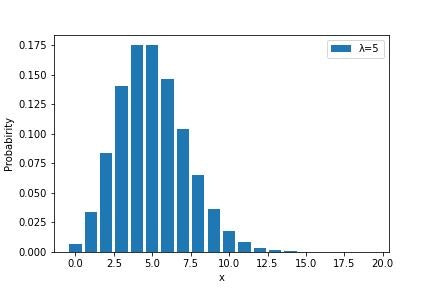
▶ポアソン分布
ポアソン分布は交通事故の数など二項分布において同じ事象ですが滅多に発生しない事象を扱う際に用います。
ポアソン分布の分布関数Poは下記のように与えられます。
Po(x|\lambda)=\frac{1}{x!}\lambda^x\exp(-\lambda)
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=\lambda\\
V[X]=\lambda
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import poisson
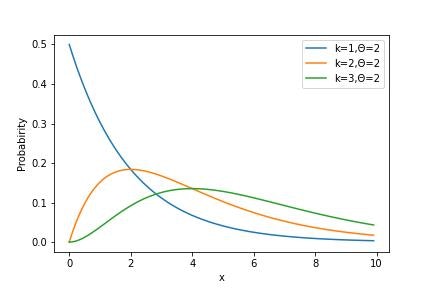
▶Gamma分布
Gamma分布は感染症の潜伏期間などを扱う際に用います。
Gamma分布の分布関数Gammaは下記のように与えられます。
Gamma(x|k,\theta)=\frac{1}{\gamma(k)\theta^k}x^{k-1}\exp\left(-\frac{x}{\theta}\right)\\
\Gamma(z)=\int^\infty_0\mathrm{d}[t^{z-1}e^{-t}]
またその期待値E[X]と分散V[X]はそれぞれ下記のようになります。
E[X]=k\theta\\
V[X]=k\theta^2
pythonにて用いる場合には下記のようにライブラリを呼び出します。
from scipy.stats import gamma
■自然共役事前分布
尤度関数に用いる分布関数として「確率分布」の節で提示したような形を用いることを見ていきました。例えば、ベルヌーイ分布の場合下記のような形でかけていました。
B(x|\theta)=\theta^x(1-\theta)^{1-x}
事後分布の計算はこの尤度関数と事前分布の積の形で与えられていたことを思い返すと例えば以下のような事前分布を選ぶと事後分布の形が綺麗にかけるということがわかります。
(事前分布)=\theta^2(1-\theta)^2\\
(事後分布)=\theta^{x+2}(1-\theta)^{3-x}
このように事後分布の形が事前分布の形と同じ(べき乗の違いはあるが)になるような事前分布を自然共役事前分布といいます。これを用いることで事後分布が解析的に書くことができるため、計算が単純化されるなどのメリットがあります。
下記はそれぞれの尤度関数に対する自然共役事前分布と、その結果計算される事後分布がどのような形になるのかを記した表になります。
| 尤度関数 | 自然共役事前分布 | 事後分布 |
|---|---|---|
| ベルヌーイ分布 | Beta分布 | Beta分布 |
| 2項分布 | Beta分布 | Beta分布 |
| ポアソン分布 | Gamma分布 | Gamma分布 |
| 正規分布の平均 | 正規分布 | 正規分布 |
■MAP推定・無情報事前分布
例えばデータが正規分布に従いそうだ(つまり尤度関数が正規分布に従いそうだ)ということがわかっていると仮定します。このとき正規分布のパラメータとなっているμ及びσを求める必要があります。またこれらを用いて、事後分布を求める必要があります。この事後分布の求め方には下記のような3つの方法があります。
・自然共役事前分布を用いて手計算
・事後分布が最大の点のみを求める(MAP推定)
・MCMCを用いて事後分布をサンプリング
この中で2番目に記載した、MAP推定を見ていきます。
最大となる点を求めるとありますが、これは確率分布をp(X|Y)として、このp(X|Y)が最大となるようなX(MAP推定値)を求めます。つまり確率分布の山の頂上の点を求めます。このとき事前分布をどうするのかという問題が発生します。特に何も情報が与えられていない場合には無情報事前分布というものをよく用います。これは事後分布に影響を与えないように選ばれます。例えば平均0分散100のような広い範囲で一定値をとるような関数です。
このとき無情報事前分布を用いた場合にMAP推定を行うと下記のように変形することができることから、尤度関数と事後分布の頂点の値は一致し、MAP推定値が最尤推定値と一致することがわかります。このような尤度関数を最大化するような値、すなわち最尤推定法は従来の統計学のやり方と整合しているということがわかるかと思います。
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\theta_{\mathrm{MAP}}=\argmax_X p(X|Y)=\argmax_X p(Y|X)p(X)
ここで無情報事前分布を考えていることから、
p(X)=\mathrm{const}
と書くことができるため、
\theta_{\mathrm{MAP}}=\argmax_X p(Y|X)
これをpythonにて実装していくためにさらに変形を進めて、下記のように記載します。
まずはlogが単調増加関数であることを用いて、
\theta_{\mathrm{MAP}}=\argmax_X p(Y|X)=\argmax_X (\log p(Y|X))
次にlog(p(Y|X))の最大化と-log(p(Y|X))の最小化が同じであることを用いて、
\theta_{\mathrm{MAP}}=\argmin_X (-\log p(Y|X))
とします。この最小化はscipyのoptimizeモジュールのminimizeを用いて実行できるため、これを用います。
この形自体は任意の確率分布に対して成り立ちますが、今回の場合は尤度関数は正規分布だと仮定していることから、ここからさらに式変形を行うことができます。ここでデータYはそれぞれのデータ点x_i(i=1,・・・,N)を表現していることを考えると、
-\log p(Y|X)=-\log N(Y|X)=-\log \prod_{i=1}^N N(x_i|X)=-\sum_{i=1}^N\log N(x_i|X)
と書くことができます。
それでは実装を行います。まずはライブラリのインポートと図のスタイルを指定します。
#ライブラリのインポート
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt
%matplotlib inline
#グラフの見た目変更
plt.style.use("ggplot")
次に今回用いるデータを生成します。μ=5,σ=3の正規分布に従うデータを下記では1000個作成しています。そのため、最終的なMAP推定の結果としては正規分布の場合は最大値をとる点が平均値μと一致するはずなので、このμ=5に近い値が得られれば推定成功となります。
#データの作成
#データ数
N=1000
#乱数のSeedを固定
np.random.seed(999)
#μ=5,σ=3の正規分布に従うデータを生成
value=np.random.normal(5,3,N)
次に尤度関数を返却する関数を定義します。
def likelihood(mu,*args):
li_tmp=-np.log(stats.norm.pdf(mu,loc=args))
li=np.sum(li_tmp)
return li
この尤度関数を用いて、最小化を行います。
#最小化させる
optimize.minimize(likelihood,1,args=value)
その結果下記のような出力が得られます。結果の見方の詳細については下記のscipyの公式ページを参照ください。今回注目したいのは一番下に出力されている値で、これが最小値を与えるとき値、すなわちMAP推定値となります。この場合は4.94369474という値になっており、当初想定していた、5と近い値が出ていることがわかります。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html#scipy.optimize.OptimizeResult
fun: 5719.839975249819
hess_inv: array([[0.001]])
jac: array([0.])
message: 'Optimization terminated successfully.'
nfev: 8
nit: 3
njev: 4
status: 0
success: True
x: array([4.94369474])