※このエントリには漫画「嘘喰い」に登場するゲームのルールの記載あるのでご注意ください。
先日「嘘喰い」を最後まで読みまして、最終章の「ハンカチ落とし」ゲームについては単純化すれば最適な戦略(ナッシュ均衡戦略)を求められそうだったのでやってみます。
ハンカチ落としゲーム
漫画内でのルール
二人で行い、片方がハンカチを落とす側、もう片方が振り返って確認する側です。
ゲームの詳細の解説は以下になります。後半エグいのでゲームの戦略にだけ興味がある方は飛ばしてください。
(Wikipedia 「嘘喰い」より)
ハンカチを落とす方を「ドロップ側」振り向いてハンカチが落ちたのを確認する方を「チェック側」とし、交互に担当していく。進行には時報を利用する。1ターンは1分間とし、ドロップ側は必ずその時間内に落とさなければならず、チェック側は必ず一度だけ振り向かなければならない。ドロップ側がハンカチを落とした瞬間からチェック側の「座視の際」がスタート、容器の中蓋が開きシリンダーに「臨死薬」が溜まっていく。振り向いてハンカチが落ちていればチェック成功となり中蓋が閉じるが逆に落ちていなければ「ペナルティ」が発動。「その時点で溜まっている臨死薬+1分間で溜まる量」をその場で注射(シリンダーに臨死薬が5分間分溜まった場合も即注射)される。そして脈拍が止まったのを確認してから「臨死」がスタート。ペナルティ秒数を消化したら臨死薬と対になる成分の「蘇生薬」を注射した上で15回限定の心臓マッサージ(約10秒間ほど)を行い、それで蘇生できたらゲーム続行、できなければ勝負あり。
簡略化ルール
上記ルールを大まかにまとめると、このゲームは2つの要素に分かれます。
- 一対戦(一分間)のハンカチ落としゲームの勝敗により、得点が与えられる
- 役割を入れ替えながらゲームを繰り返して、得点が一定量を超えたら勝利
本エントリではこのうち1の一回分のハンカチ落としゲームに絞って戦略を考察します。
得点はハンカチを落とす「ドロップ側」から見た値とし、細かい点を簡略化して以下のようなルールを考えます。
- 時刻 $t = 1,2,..,N$ のそれぞれで「ドロップ側(以下D)」「チェック側(以下C)」が行動を決定
- Cが振り向いた時刻を $i$、 Dがハンカチを落とした時刻を $j$ とする
- $i < j$ のとき、Dは 「落とされていないのに振り向いた」得点 $M$ 点 を獲得
- $i \geq j$ のとき、Dは 「落とされてからの経過時間」得点 $i - j$ 点 を獲得
- $N \geq 1, M \geq 1$
漫画では両者が同時($i = j$)だった場合には最低点の1点という扱いになっていますが、後ほど連続時間ゲームに拡張する上で同時を特別扱いすることが難しいため0点とします。
結論
1分間で連続時間拡張して、ペナルティ$M$が1分相当のとき、このゲームのナッシュ均衡戦略は
- ドロップ側は開始と同時に 約36.8% の確率で落とし、それ以降の時刻(1秒ごと)に落とす確率は 約0.6% から 約1.6% まで段々大きくしていく
- チェック側がある時刻に落とす確率は 約1.6% から 約0.6% までだんだん小さくしていき、最後まで振り返らない確率は 約36.8%
値を数式で表現すると、
- ドロップ側は開始と同時に $\frac{1}{e}$ の確率で落とし、それ以降は時刻 $t \space (0 \leq t \leq 1)$ に落とす確率密度は $e^{t - 1}$
- チェック側は時刻 $t$ に振り返る確率密度は $e^{-t}$ で、最後まで振り返らない確率は $\frac{1}{e}$
です。
解析
概観
このゲームでは、相手が既知の決定的戦略を取る場合にはこちらも対抗する決定的戦略を取ることで報酬を最大化できます。
例えばCが最後まで振り向かない戦略を取る場合、Dはゲーム開始と同時に(時刻 $t = 1$ で)ハンカチを落とすのが最善です。
逆にDが時刻 $t$ にハンカチを落とす場合、Cは同じ時刻 $t$ に振り向くのが最善です。さらにそのDの戦略に対しては時刻 $t$ までには落とさずいるのが最善です。
このように、相手の決定的な戦略に対する最適戦略を考え続けると堂々巡りすることになります。
ナッシュ均衡
「ナッシュ均衡戦略」はある種の最適性の一般的な定義であり、以下のように定義されます。
全てのプレーヤーにとって、戦略を変更することで得をしない状態
ナッシュ均衡になるような各プレーヤーの戦略をナッシュ均衡戦略と呼びます。
例えば○×ゲームやオセロのように一人ずつ順番にプレーするゲームにおけるナッシュ均衡戦略は、両者が最善の手を出し続ける戦略です。
一方でじゃんけんのような同時性のあるゲームにおいては一般的には混合戦略(確率的な戦略)がナッシュ均衡戦略となります。じゃんけんにおいてはグー、チョキ、パーからランダムに選んで出し続ける戦略がナッシュ均衡で、相手がこの戦略を取る以上、搾取することは不可能になります。
戦略定式化
このゲームにおける戦略を以下のように定義します。
- C側が時刻 $t$ に振り向く確率 $P_t$
- D側が時刻 $t$ にハンカチを落とす確率 $Q_t$
さらに表記の単純化のため、それぞれ行動を起こさずに終了した場合には時刻 $N+1$ に行動を起こしたことにします。(この問題設定では得点の定義を変更する必要はありません)
つまり$P,Q$それぞれの拘束条件として
\sum_{t=1}^{N+1} P_t = 1 \\
\sum_{t=1}^{N+1} Q_t = 1
このときD側から見た得点の期待値 $R$ は式(1)で表されます。
\begin{align}
R(P, Q) &= M \sum_{i=1}^{N+1} P_i (1 - \sum_{j=1}^{i} Q_j) + \sum_{i=1}^{N+1} P_i \sum_{j=1}^{i} Q_j (i - j)\\
&= \sum_{i=1}^{N+1} P_i (M + \sum_{j=1}^{i} Q_j (-M + i - j))
\end{align}
整理前の式にて、時刻 $i$ に振り向いたときに、左側の項がまだハンカチが落とされていない場合、右側の項が時刻 $j \space (\leq i)$ にすでに落とされていた場合です。
ナッシュ均衡の計算
ナッシュ均衡の定義から、確率の拘束条件を満たす中で期待得点を最大化(最小化)する $P, Q$ を求めれば良いです。
仮に全ての $t$ について $0 < P_t < 1, \space 0 < Q_t < 1$ ならば、ナッシュ均衡の $P, Q$ は拘束条件の下で式 $R$ における停留点(=微分して0になる点)となっているはずなので、ラグランジュの未定乗数法を適用できます。
Wikipedia「ラグランジュの未定乗数法」
未定乗数法では以下の偏微分=0の式から $P, Q$ を求めます。
\begin{align}
&F(P, Q, \gamma, \lambda) = R(P, Q) - \lambda (\sum_{i=1}^{N+1} P_i - 1) - \gamma (\sum_{i=1}^{N+1} Q_i - 1)
\\
&\frac{\partial F}{\partial P_t} = \frac{\partial F}{\partial Q_t} = \frac{\partial F}{\partial \lambda} = \frac{\partial F}{\partial \gamma} = 0
\end{align}
前二つを展開して整理
\begin{align}
&\frac{\partial F}{\partial P_t} = M + \sum_{j=1}^{t} Q_j (-M + t - j) - \lambda = 0\\
&\sum_{j=1}^{t} Q_j (-M + t - j) = \lambda - M = const.\\
&\frac{\partial F}{\partial Q_t} = \sum_{i=t}^{N+1} P_i (-M + i - t) - \gamma = 0\\
&\sum_{i=t}^{N+1} P_i (-M + i - t) = \gamma = const.
\end{align}
この式の意味するところは、時刻 $i$ と $j$ に対して $(P_i, P_j)$ を $(P_{i+d}, P_{j-d})$ に変化させても得点の期待値が変化しないということなので、ナッシュ均衡の定義に従っています。(未定乗数法を経由せずとも直接この式を立てられる)
この式の $t$ と $t + 1$ での差分から、$1 \leq t \leq N$ にて
\begin{align}
\frac{\partial F}{\partial P_t} &= \frac{\partial F}{\partial P_{t+1}}\\
\sum_{j=1}^{t} (-M + t - j) Q_j &= \sum_{j=1}^{t+1} (-M + t + 1 - j) Q_j\\
0 &= - M Q_{t+1} + \sum_{j=1}^{t} Q_j\\
Q_{t+1} &= \frac{1}{M} \sum_{j=1}^{t} Q_j
\end{align}
同様に
\begin{align}
\frac{\partial F}{\partial Q_t} &= \frac{\partial F}{\partial Q_{t+1}}\\
\sum_{i=t}^{N+1} (-M + i - t) P_i &= \sum_{i=t+1}^{N} (-M + i - t - 1) P_{i+1}\\
- M P_t &= -\sum_{i=t+1}^{N+1} P_j\\
P_{t} &= \frac{1}{M} \sum_{i=t+1}^{N+1} P_i
\end{align}
$P, Q$ それぞれに対して漸化式が定まったので、これと合計が1という条件を合わせれば答えが出ます。
ナッシュ均衡戦略(離散時間)
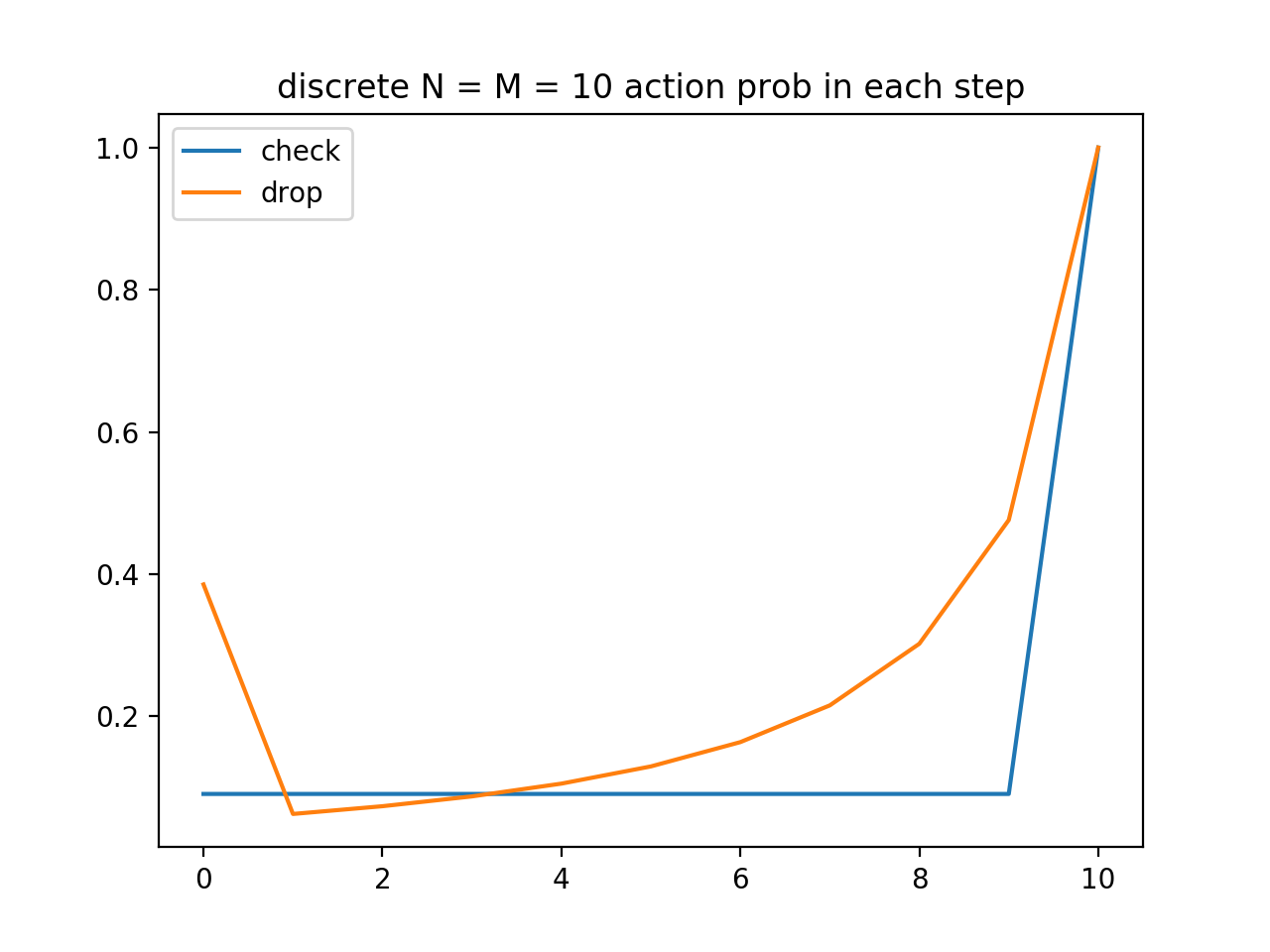
作中では $N = M = 60$ ですが見やすさのため10としています。
N = M = 10
# Q求解
Q, sumQ = [1], 1
for i in range(N):
Q.append(sumQ / M)
sumQ += sumQ / M
Q = [q / sumQ for q in Q]
# P求解
P, sumP = [1], 1
for i in range(N):
P.append(sumP / M)
sumP += sumP / M
P = list(reversed(P))
P = [p / sumP for p in P]
# 図示
import matplotlib.pyplot as plt
plt.plot(P, label='check')
plt.plot(Q, label='drop')
plt.legend()
plt.show()
チェック側(青)が時刻 $t$ に振り返る確率(割合)、ドロップ側(オレンジ)が時刻 $t$ にハンカチを落とす確率(割合)を図示しました。一番右端が最後まで何もしない確率を表しています。
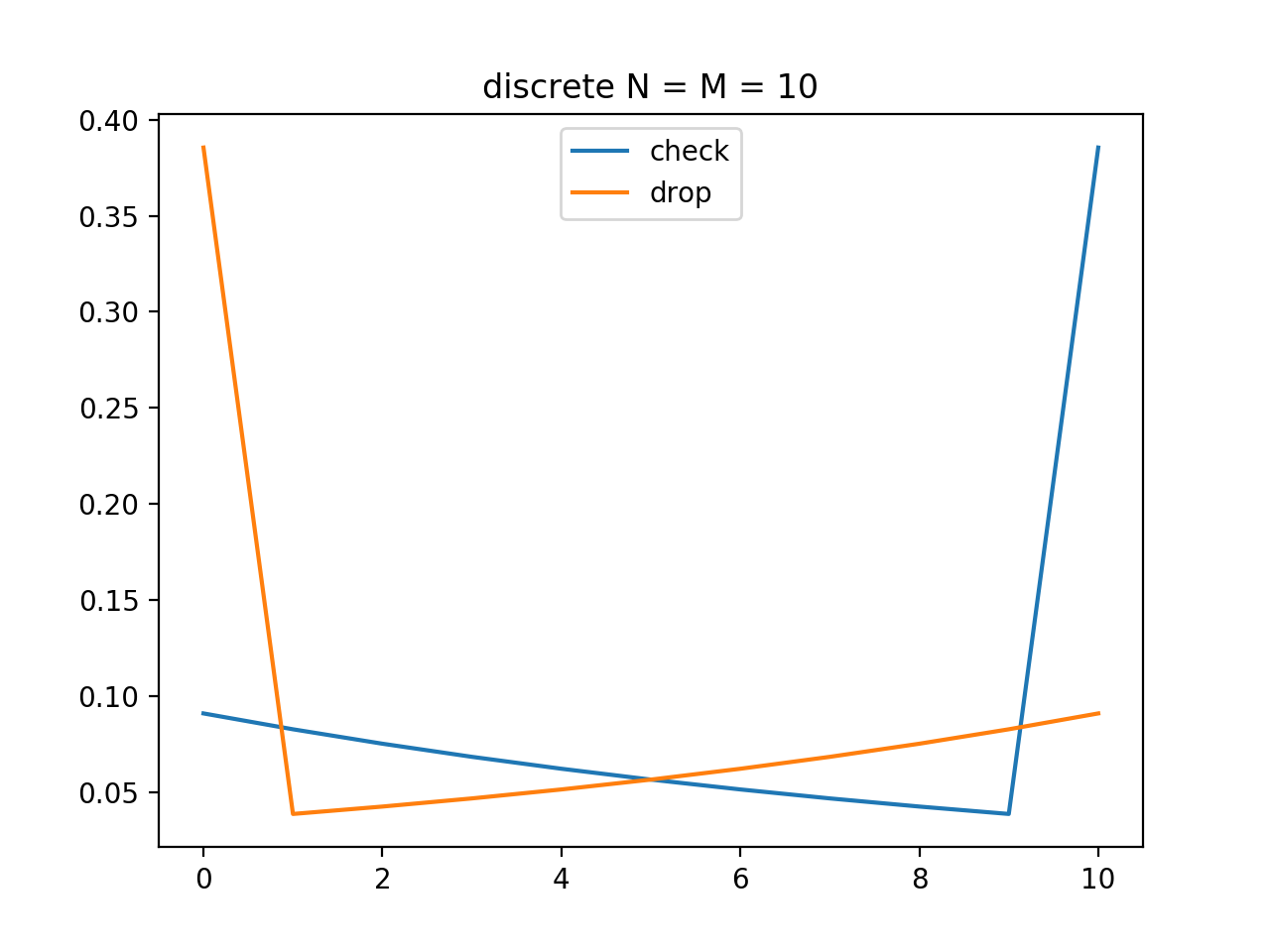
チェック側はある一定確率を「最後まで振り向かない」( $P_{t+1}$ の確率が最後まで振り向かないことを表す)に振ってあとは振り向く確率を段々と下げていき、一方ドロップ側は反対で「開始直後に落とす」確率が大きくあとは単調増加で確率を上げていく戦略となりました。
ナッシュ均衡戦略の解釈
$P, Q$ はどの時刻に行動を起こすのか分配する確率であり、「その時刻になったときに行動を起こす確率」とは違います。後者の確率による戦略表記をC側 $S$ 、D側 $T$ とすると
S_t = \frac{P_t}{1 - \sum_{i=1}^{t-1} P_t}\\
T_t = \frac{Q_t}{1 - \sum_{i=1}^{t-1} Q_t}
となり、実はC側の戦略はそれぞれの時刻で独立に同じ確率で振り向くかどうか決めているのと同じだとわかります。
チェック側が最後まで振り向かない確率が38%程度を占めるのは、振り向いてもしまだ落とされていなかった場合のペナルティが大きいため、振り向かない戦略が有効だからと考えられます。
一方でドロップ側が開始直後に落とす確率も同じく38%と大きいことはそれほど自明では無いです。開始直後に落としてしまっては相手の振り向き失敗を誘うことは不可能になりますし。
試しに振り向き失敗場合の得点 M を大きくしてみます。
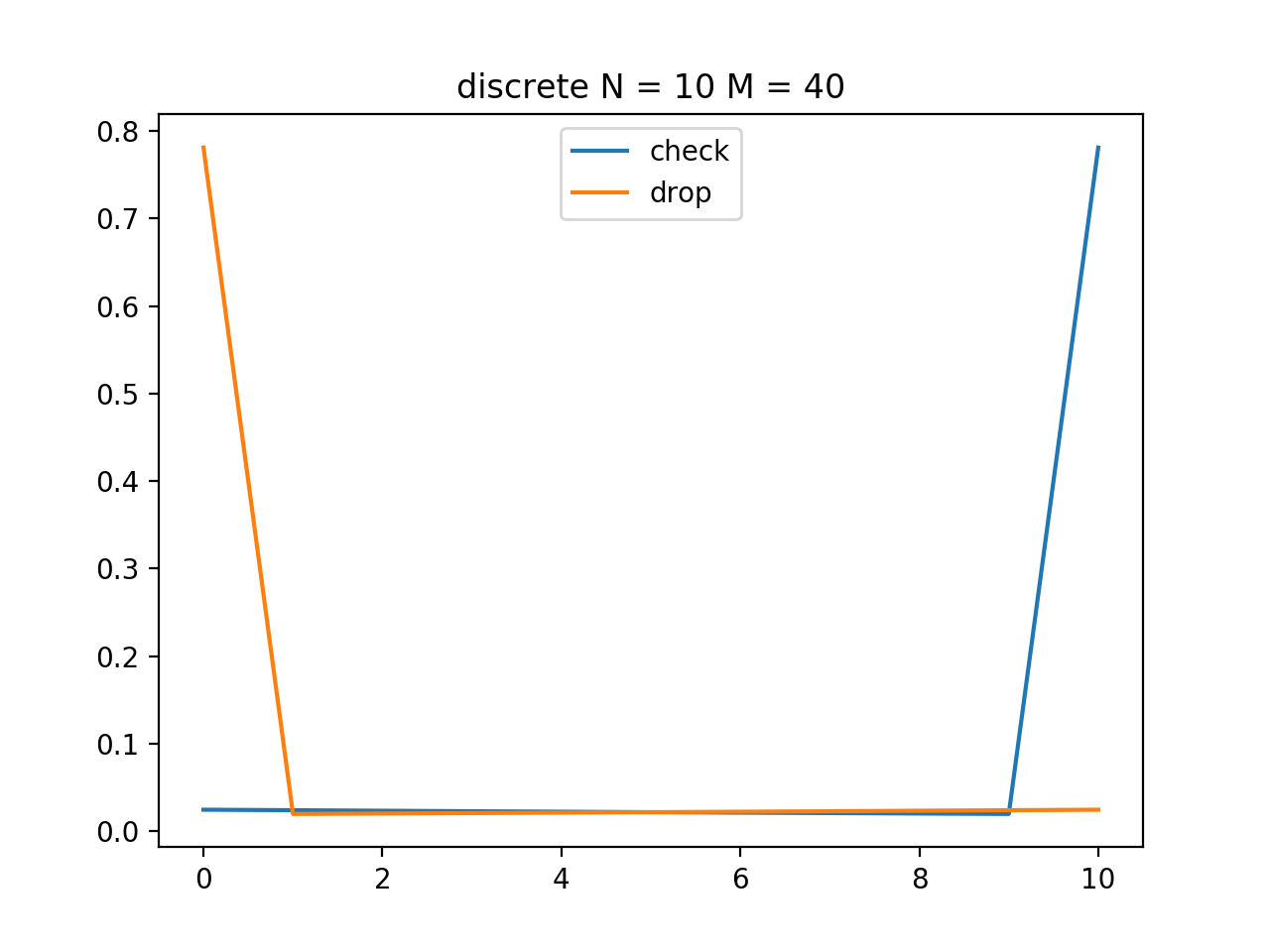
図の通り、「最後まで振り向かない」確率が大幅に上昇し同じように「開始直後に落とす」確率も上昇しました。
この結果から次のような解釈ができます。
- 振り向き失敗の得点が大きいほど、チェック側は振り向かなくなる
- ドロップ側は相手の振り向き失敗に期待できなくなり、早めに落とすことで少しでも得点を稼ぐことの価値が相対的に大きくなるため、開始直後に落とすようになる
実際に両者がこの戦略を取った場合の報酬を計算すると、 $N = M = 10$ で6.14点程度になります。
この戦略を $P_{*}, Q_{*}$として片方の戦略のみ変化させてみましょう。
# P, Q として P*, Q* が計算されているとする
def reward(P, Q):
# 添字が 0 ~ N になるので注意
return sum([P[i] * (M + sum([Q[j] * (-M + i - j) for j in range(i + 1)])) for i in range(N + 1)])
# 片方の戦略を変更
print(reward(P, Q))
print(reward(P, [0] * N + [1]))
print(reward(P, [1 / (N + 1)] * (N + 1)))
print(reward([1] + [0] * N, Q))
print(reward([1 / (N + 1)] * (N + 1), Q))
実行結果
6.144567105704683
6.144567105704684
6.144567105704682
6.144567105704683
6.144567105704682
相手の戦略によって得点期待値は変化していません。
ナッシュ均衡の定義通りではありますが、じゃんけんと同じく、ただ負けないだけで平均以上勝つこともありません。
少々むなしいですがナッシュ均衡とはそういうものです。
作中のゲームに近い繰り返しのあるゲームならば、勝っている側が安全策を取ったりなどダイナミックな戦略の変化が見られるはずです。…が、どちらにせよナッシュ均衡がその時点での期待勝率を上げも下げもしない地味な戦略であることは変わりありません。上手い話は無いというわけです。
想像を超えた方法による劇的な勝利を望む方はぜひ 「嘘喰い」の本編を一巻から読む ことをお勧めします!
漸近的挙動と連続時間への拡張
さて、離散の場合のナッシュ均衡戦略が求まりましたが、 $N(= M)$ を大きくしてみると、「振り向かない確率」「開始直後に落とす確率」はほとんど変化なく 定数$\frac{1}{e}$ に収束していき、それ以外の時刻で行動を起こす確率は0に近づいていくことがわかります。
そのため、ゲームを連続時間に拡張すると 開始時点と終了時点が特異点でありそれ以外の時刻では連続な確率密度関数 が得られることが期待できます。
ゲームの定義を以下のように変更します。
- 時刻 $0 \leq t \leq 1$ で落とすか振り向くか決められる。
- 時刻 $i$ に振り向き $j$ に落とす場合の得点 $i \geq j$ のとき $i - j$、$i < j$ のとき $K$ ($\frac{M}{N}$に相当)
このとき、離散の場合の極限と特異な確率 $\frac{1}{e}$ から $P(t)$ と $Q(t)$ は積分方程式で表せます。
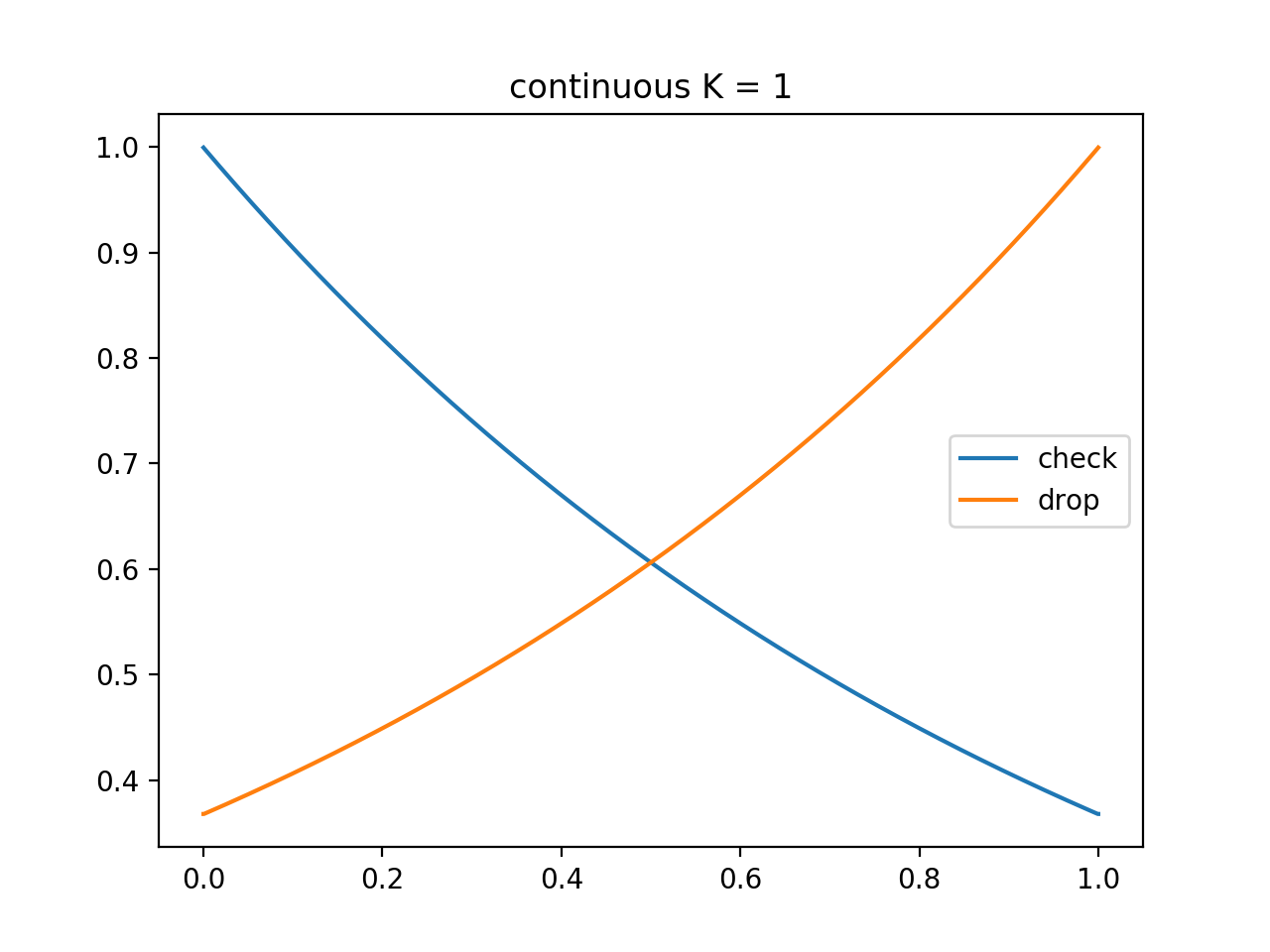
$K = 1$ のとき
\begin{align}
P(t) &= e^{-1} + \int_t^1 P(x) dx\\
Q(t) &= e^{-1} + \int_0^t Q(x) dx
\end{align}
これを解いて
\begin{align}
P(t) &= e^{- t}\\
Q(t) &= e^{t - 1}
\end{align}
ただし「振り向かない確率」「開始直後に落とす確率」はそれぞれ $\frac{1}{e}$ で、上記の確率密度関数には含まれません。
情報の非対称性は無視して良いか?
ここまで特に言及しませんでしたが、ハンカチ落としではDとCに情報の非対称性があります。
Cは何も情報を得ずにゲームが終了しますが、Dは相手がまだ振り向いていないという情報を得ているので、「ゲーム開始時に戦略 $Q$ にしたがってランダムに決定」だけでなく随時戦略をアップデートすることが可能です。
ただ残念ながらそれによってナッシュ均衡戦略が変わることはありません。
というのも、時刻 $t$ におけるDの戦略は、時刻 $t - 1$ までにまだゲームが終わっていないことが前提となっており、それゆえその時点で得ることができる情報はそもそも一通りしかないためです。
おわりに
ハンカチ落としのナッシュ均衡は綺麗な数式で表せる事がわかりました。
皆さんもハンカチ落としで遊ぶ、または命を賭けた大勝負を行う場合には、ナッシュ均衡戦略を頭に入れた上で大きなミスなく勝負所を迎えられるようにしましょう。