問題設定
強化学習の方策の急峻化を防ぐため、過去のエピソード内の方策(挙動方策)とのカルバック・ライブラー(KL)情報量ロスを加え、学習をゆっくり進める。
このとき方策全体ではなく選んだ行動の選択確率のみ得られているとき、どんなロスを使うか?の話。
結論
選ばれた行動 $a$ の挙動方策 $p_a$、推定方策 $q_a$ として、
1-action forward KLのロスはこの式を使う。
\frac{1}{q_a} (p_a - q_a) \log {\mathbf p_a}
reverse KLなら次の式。
\frac{p_a}{q_a}(\log p_a - \log q_a) \log {\mathbf p_a}
ただし勾配計算は太字部分のみ。
前提
KL正則化は強化学習で出力の安定化/行動の多様性向上に使う手法。
ここでは学習するエピソード内の方策(挙動方策)に近づける。
KL正則化
学習中の方策と挙動方策のカルバック・ライブラー情報量を小さくするロスを追加して学習する。
D(Q, P) = \sum_i q_i \space (\log q_i - \log p_i)
Pをモデル出力でQをバッファ内の方策とするのがforward KL、逆にするのがreverse KL。
forward KLを使うことが一般的だが、用途次第。
1-action設定
リプレイバッファ内に、方策の確率分布全体でなく選んだ行動の確率だけ記録する方法。
行動数が多い時のメモリ効率を上げたい/そもそも全行動の確率がわからない場合などに使う。
オフポリシー学習で使う重要度サンプリングは選んだ行動の確率だけで可能。
勧めない 1-action KL
エピソード内で選択された行動を $a$ として
\log q_a - \log p_a
バッファ内の行動は確率 $q_a$ で選択されるので期待値は $\sum_a q_a \space (\log q_a - \log p_a)$ で一致。
ただ、$\log q_a$は定数なので実質 $-\log p_a$ がロスだが、このロスは選ばれた行動をさらに選ばれやすくする ($\log p_a$の最大化)。そのため、学習中に偶然多く選ばれた行動が選ばれ続けることになり、とくにエピソード生成数が少ない学習で学習を阻害しうる。
微分
$X$ を最終層の出力、$P = softmax(X)$ とする。
forward KL
全行動を使ったKL
\begin{align}
\frac{\partial}{\partial x_i} D(Q, P) &= - \sum_j q_j \frac{\partial}{\partial x_i} \log p_j \\
&= -q_i + \sum_j -q_j \cdot -p_i \\
&= p_i - q_i
\end{align}
1 action KL
\begin{align}
\frac{1}{q_a} (p_a - q_a) \space \frac{\partial}{\partial x_i} \log p_a
&=
\left\{
\begin{array}{ll}
(p_a - q_a) \space (1 - p_i) & (i = a) \\
- \space (p_a - q_a) \space p_i & (i \neq a)
\end{array}
\right.
\end{align}
期待値
\begin{align}
\sum_a q_a \space \frac{1}{q_a} (p_a - q_a) \space \frac{\partial}{\partial x_i} \log p_a
&= p_i - q_i -p_i \space (\sum_a p_a - \sum_a q_a) \\
&= p_i - q_i
\end{align}
$p_a = q_a$ のときロスの微分は0でありバイアスがなく、期待値が一致する。
reverse KL
reverse: 全行動を使ったKL
\begin{align}
\frac{\partial}{\partial x_i} D(P, Q)
&= \sum_j \frac{\partial}{\partial x_i} p_j (\log p_j - \log q_j) \\
&= \sum_j (\log p_j - \log q_j) \frac{\partial}{\partial x_i} p_j + p_j \frac{\partial}{\partial x_i} \log p_j \\
&= \sum_j (\log p_j - \log q_j + 1) \space p_j \space \frac{\partial}{\partial x_i} \log p_j \\
&= (\log p_i - \log q_i + 1) p_i - p_i \sum_j (\log p_j - \log q_j + 1) p_j \\
&= (\log p_i - \log q_i) p_i - p_i \sum_j (\log p_j - \log q_j) p_j
\end{align}
reverse: 1 action KL
\begin{align}
\frac{p_a}{q_a}(\log p_a - \log q_a) \frac{\partial}{\partial x_i} \log p_a
&=
\left\{
\begin{array}{ll}
p_a \space (\log p_a - \log q_a) \space (1 - p_i) & (i = a) \\
- \space p_a \space (\log p_a - \log q_a) \space p_i & (i \neq a)
\end{array}
\right.
\end{align}
期待値
\begin{align}
\sum_a q_a \space \frac{p_a}{q_a} (\log p_a - \log q_a) \space \frac{\partial}{\partial x_i} \log p_a
&= (\log p_i - \log q_i) p_i -p_i \sum_a (\log p_a - \log q_a) p_a
\end{align}
$p_a = q_a$ のときロスの微分は0でありバイアスがなく、期待値が一致する。
注意点
こちらのロスは $p$ や $q$ の値が小さい時、勾配の絶対値が大きくなるので、そうならないために実用上はロスや勾配のクリッピングを行なった方が安全。
実験
勾配の期待値が一致することの実験
結果例(一部)
full
[ 0.0161, 0.0747, -0.0126, -0.2587, 0.1927, -0.0081, 0.0059, -0.0100]
expected
[ 0.0158, 0.0752, -0.0125, -0.2575, 0.1919, -0.0087, 0.0055, -0.0097]
多数回のロスの勾配を平均してほぼ一致。
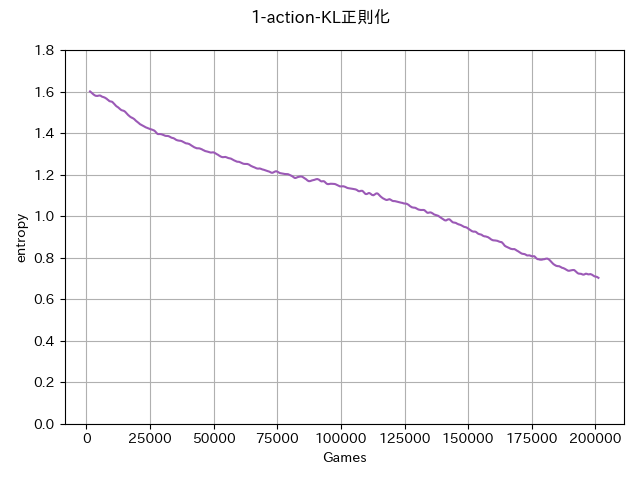
強化学習によるエントロピー変化量の実験
HandyRLのTicTacToe環境において正則化なし/KL正則化ロスあり実装
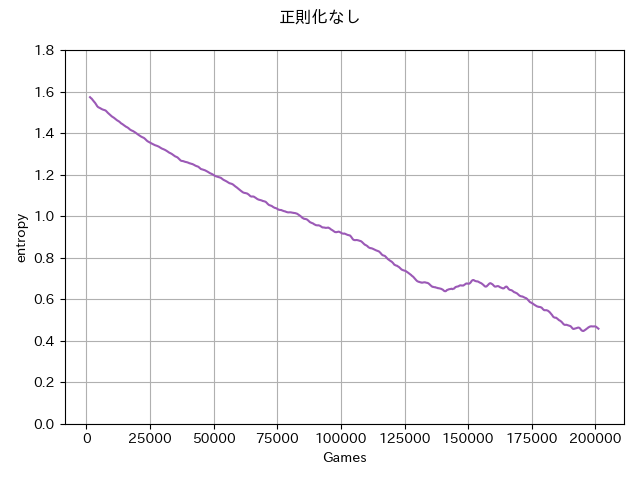
KL正則化を入れることで方策エントロピー減少がゆっくりになっている。
学習結果も比較的安定しているように見えたが、結論を出すには多数の試行が必要なのでぜひお試しを!