まず結論から
分位点の計算は
- 簡単な方法 クイックセレクトのライブラリを使う
- 同じデータから何度も行う場合は予めソートする
- データの貯め方も自由なら二分探索木がスケール可能
- 速度、メモリ至上主義の特殊な用途なら近似計算
分位点
分位点(分位数、分位値、quantile)はデータを小さい順に並べた時に、前から数えてpの割合(O<=p<=1)の所のデータの値です。
(Wikipedia 分位数) https://ja.wikipedia.org/wiki/%E5%88%86%E4%BD%8D%E6%95%B0
代表的な統計量である最小値、最大値、中央値はそれぞれquantile(0)、quantile(1)、quantile(0.5)となり、これらをより一般化した概念と言えます。
分位点の計算量
中央値などの分位点を正確に計算するには、基本的には全てのデータを保存することになりますので、データ数Nに対して空間計算量は O(N) 必要になります。
時間計算量は、単純にデータ全てをソートしてから値を選ぶ場合には O(N log N) かかることになります。
データセットが固定の場合には一度ソートしてしまえばそれ以降はO(1)で良いのですが、
逐次的にデータが増えて適宜分位点を求めるような状況では理想的とは言えないでしょう。
以下では時間計算量を減らすためのアルゴリズムの工夫と、さらには近似アルゴリズムによって空間計算量も減らす手法を紹介します。
自分の実装は全て https://github.com/YuriCat/test/blob/master/quantile/quantile.cpp にあります。
分位点計算の基本
あるデータに対する p-分位点 を求める簡単なC++コードは以下のようになるでしょう。
template <typename T>
double quantile(vector<T>& data, double p)
{
if (data.size() == 1) return data[0];
double position = p * (data.size() - 1);
int n = min(int(position), data.size() - 2);
// n,n+1番目のデータが欲しい
double r = position - n; // 余り
sort(data.begin(), data.end());
return data[n] * (1 - r) + data[n + 1] * r;
}
値の区間はデータの個数 - 1だけあるので、区切って何番目のデータが要るのか調べます。
最小値や最大値の場合は値が1つ得られれば良いですが、一般的には2つの値の重み付け平均を取ります。
データ数が0の場合は分位点は定義出来ず、
またデータ数1の場合も例外で唯一の値をそのまま返す処理に分岐することに注意が要ります。
クイックセレクト
まずはデータをソートするより効率よくn番目の値を得ることを考えます。
クイックソートは基準となる値より大きいものと小さいものに分割して再帰的にソートを行います。
この時データの個数から、n番目の値がどちらの範囲に含まれるかは明白なので、もう片方は無視してそちらだけ調べて行けば、全体をソートするより効率よくn番目の値を得ることができます。
さらにたまたまn番目をピボットとして引き当てれば、それ以降精査せずに終了出来ます。
これはクイックセレクトと呼ばれるアルゴリズムで、時間計算量が平均でO(n)、最悪でO(n^2)となります。
クイックセレクトはC++ならSTLにstd::nth_element()という実装があるのでそのまま使うことが出来ます。
以下ではnとrの計算は共通なので略記します。
template <typename T>
double quantile(vector<T>& data, double p)
{
int n = ...; double rest = ...;
nth_element(data.begin(), data.begin() + n, data.end());
nth_element(data.begin() + n + 1, data.begin() + pos + 1, data.end());
return data[pos] * (1 - rest) + data[pos + 1] * rest;
}
std::nth_elementは特殊なインターフェースで、値もイテレータも返さず指定したn番目に欲しいデータが入っている状態にして返します。
破壊的な変更であることに注意が必要です。ここでは2度目のコールではn+1番目以降しかいじらないのでn番目の値は安全です。
Pythonではnumpy.quantile()が内部でクイックセレクトを行います。
クイックソートと同じく、ピボット(半分に分ける基準の値)として変な値を引き続けなければ最悪計算量は気になりませんが、自分で実装する場合には注意が必要です。
挿入ソートによりソート済みの状態を保つ
データの追加に対して分位点の計算の頻度が多い場合には、ソートされた状態を保ちながら O(n) でデータの追加を行い、O(1)で値を引くことも考えられます。
template <typename T>
struct SortedSet
{
vector<T> data;
SortedSet()
{
data.push_back(numeric_limits<T>::lowest());
}
void insert(T value)
{
data.push_back(T(0));
int index = (int)data.size() - 1;
while (value < data[index - 1])
{
data[index] = data[index - 1];
index--;
}
data[index] = value;
}
double quantile(double p) const
{
int n = ...; double r = ...;
return data[n + 1] * (1 - r) + data[n + 2] * r;
}
};
下限以下の値を番兵として最初に入れておくと境界チェックをせずに済みます。
(寄り道)値の定義域が有限な場合
データの数は多いけれどもデータの種類は少ない、特に O~M-1 に収まるような整数の場合ならば
固定長O(M)のサイズのデータ構造を使うことも検討の余地があります。
この場合には以下の2通りの実装が考えられるでしょう。
| 用途 | アルゴリズム | 挿入計算量 | 分位点計算計算量 |
|---|---|---|---|
| 挿入メイン | ヒストグラム | O(1) | O(M) |
| 分位点計算メイン | 累積ヒストグラム | O(M) | O(log M) |
挿入メインの場合は単純なヒストグラムを構築し、分位点計算では端から順に足していくことで目的の順の値を探せます。
要求された分位が0.5より大きい場合には後ろから足して行けば良いので、実装上はO(M/2)みたいなイメージです。
分位点計算メインの場合にはヒストグラムの累積を常に求めておき、分位点計算の際には2分探索で目的の位置を探すことが出来ます。
累積ヒストグラムの場合のコード例
template <typename T, int M>
struct BoundedCumulativeHistogram
{
array<int, M> cum_histgram;
BoundedQuantileSetManyQuery()
{
cum_histgram.fill(0);
}
void insert(T value)
{
// v以下の値の個数を更新
for (T v = value; v < M; v++)
{
cum_histgram[v]++;
}
}
double quantile(double p) const
{
int n = ...; double r = ...;
auto itr0 = lower_bound(cum_histgram.begin(), cum_histgram.end(), n + 1);
T value0 = distance(cum_histgram.begin(), itr0);
if (cum_histgram[M - 1] == 1) return value0; // データが1つのみの時
auto itr1 = lower_bound(itr0, cum_histgram.end(), n + 2);
T value1 = distance(cum_histgram.begin(), itr1);
return value0 * (1 - r) + value1 * r;
}
};
二分探索木
二分探索木は平均でデータの挿入にO(log N)、データのn番目の大きさの値を得るのにO(log N)で良いので、データが絶えず増え続け、分位点も絶えず必要な場合には適したデータ構造です。

(Wikipedia 二分探索木 より)
https://ja.wikipedia.org/wiki/%E4%BA%8C%E5%88%86%E6%8E%A2%E7%B4%A2%E6%9C%A8
同じデータが複数来た場合にはノードに個数を記録すれば良いので、値の定義域のサイズMでも時間・空間計算量を抑えることが出来ます。
今回はデータの削除や平衡性を考慮しない単純な実装で行った限りですが、実験では使えそうな結果を出しています。
2つの値を得ることを前提にした二分探索
さて計算量の議論とは関係が無いですが、分位点を求めるために2つの値を得るのに、二分探索を2回繰り返すのは明らかに無駄です。
特に分位点の計算では順序が連続した値が欲しいだけなので、本来は一度の二分探索+αで十分なはずです。
その点を考慮して、「クイックセレクト」と「二分探索木」では2倍弱の高速化が出来ます。
P^2 アルゴリズム
P^2 (P-Square) アルゴリズムは、データを挿入する際に分位点の近似値を絶えず更新していくアルゴリズムです。
https://www.cse.wustl.edu/~jain/papers/psqr.htm
データ構造は、
1.「分位点の値の近似値」
2.「分位点の近似値の(累積的な)全体順位」
3.「分位点の値の理想的な全体順位」
(4.「分位点の値の理想的な全体順序」の差分値)
を持ち、新しく挿入されたデータが1のどこに入るかによって、2を更新(データより大きい値の分を1ずらす)します。
2は現在の分位点の推定値に対して、正しい順序を示す訳ではないですが、これまでの累積として分位点の推定が上手く行っているかの指標になります。
そのため2が3に近くような方向に、随時1の推定を2次近似または1次近似によってずらして行きます。これがアルゴリズムの概略です。
実際に使用した感じでは、一様分布に対してならまあまあの値を返してくれる、という感じです。
ただし、近似の際に最小値や最大値も用いるため、定義域が有界で無い場合には端の観測値に引っ張られるのが弱点です。
詳しくは発表論文やその他の解説があります。が、発表論文の図中のアルゴリズムは細部にミスがあって修正が要りました。
↓0~100の一様な実数の分位点を推定していく図(最初の推定値を10,30,50,70,90とする)
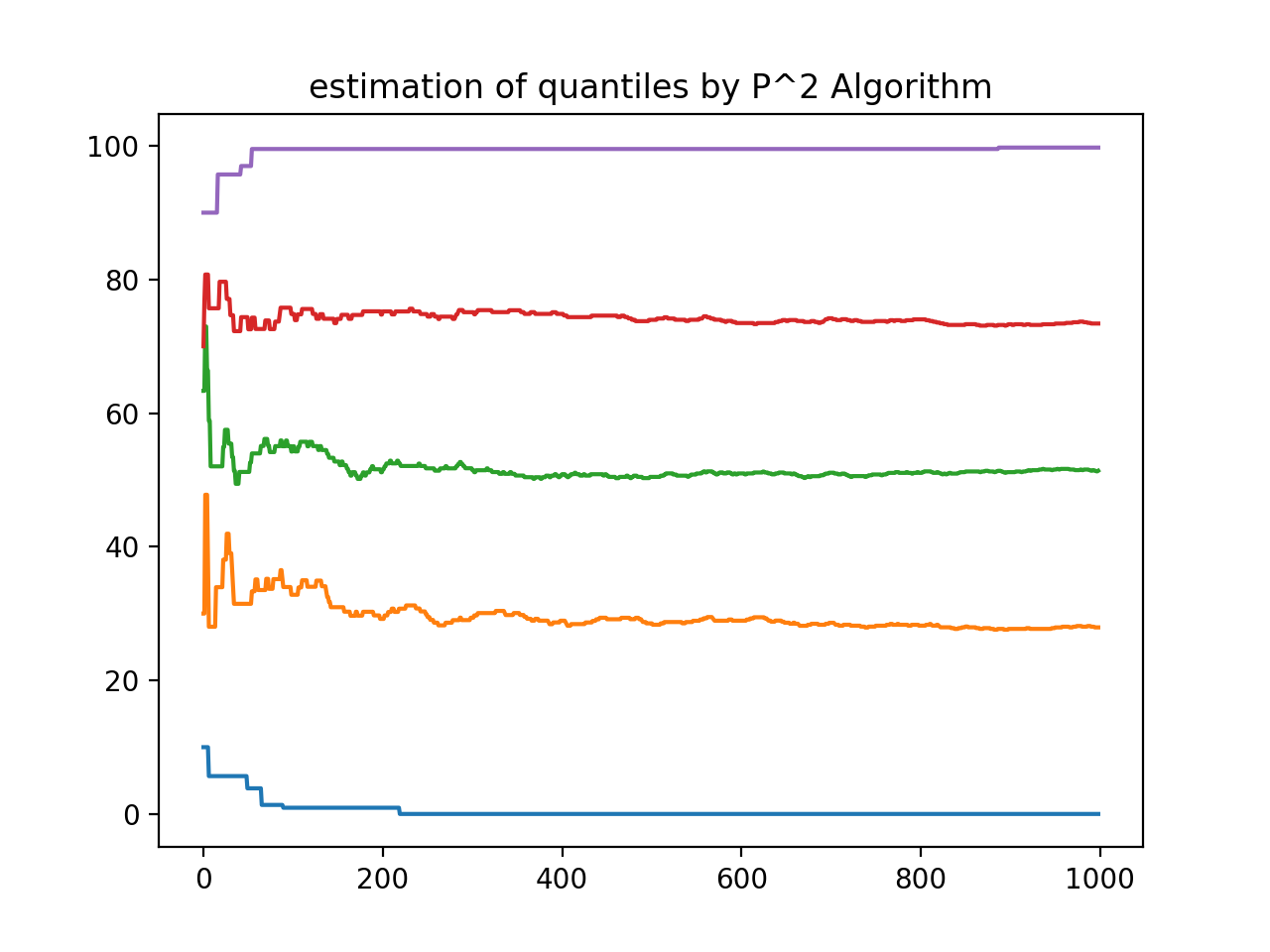
時間計測
各データはM未満の非負整数の一様乱数とします。
データ(全部でK個)を1個ずつ挿入し、その度ごとに何度か(L回)0~1の一様乱数に対する分位点計算を行い全体の時間(単位は秒)を記録します。
乱数列は予め作っておくのでそのコストは含まれていません。
4通りのパラメータ設定で、この試行を各10回行い平均を取ったものが以下の表です。
それぞれの実験条件は、
①基準 ②分位点計算多め ③データ範囲広め ④データ多め
の試行となります。
アルゴリズムはここまで説明したものですが、特に「クイックセレクト自作」「二分探索木」には二分探索を一度で済ます高速化をかけています。
| アルゴリズム | ① M=10^4 K=10^4 L=1 |
② M=10^4 K=10^4 L=10^2 |
③ M=10^6 K=10^4 L=1 |
④M=10^4 K=10^6 L=1 |
|---|---|---|---|---|
| ソート | 1.7 | 1.7 | 1.6 | - |
| クイックセレクトSTL | 0.18 | 8.5 | 0.18 | - |
| クイックセレクト自作 | 0.060 | 6.7 | 0.066 | - |
| 挿入ソート | 0.0097 | 0.013 | 0.015 | - |
| 固定長ヒストグラム | 0.0097 | 1.0 | 1.0 | 0.98 |
| 固定長累積ヒストグラム | 0.0068 | 0.10 | 1.0 | 0.89 |
| 二分探索木 | 0.0017 | 0.091 | 0.0021 | 0.21 |
| P^2アルゴリズム | 0.00036 | 0.0031 | 0.00034 | 0.029 |
結果から、正確な分位点計算を行う中では二分探索木がかなり強いことがわかります。
また固定長のデータ構造も、M=10^6でもそれなりに動いているところを見ると十分用途がありそうです。
またソートは1度行ってしまえばデータの追加までは何もしなくて良いので、挿入ソートの場合も含め
分位点計算多めの場合では強いですね。
ただデータ数10^6ではかなりの長時間がかかっているので、データ数が多い場合には辛いようです。
クイックセレクトもデータ数が多い場合は死んでいますが、多数回計算するのでなければ十分使えそうです。
P^2アルゴリズムは常にO(1)で動きますが、実際的な計算時間も圧倒的に短いので、
大体の値がもらえれば十分な場合には利用価値があると言えそうです。
データ構造とアルゴリズム Advent Calendar 2018
本稿は2018年のAdvent Calendar用に投稿したものです。
投稿年月日は見なかったことにしてください。
https://qiita.com/advent-calendar/2018/str
https://qiita.com/advent-calendar/2018/str2