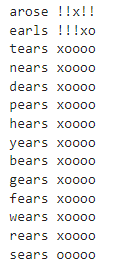Wordle
最近ツイッターでGithubの草が生えているみたいなツイートが流れてます。
これは進捗を生んでいるのではなくて、Wordleというゲームで遊んでいます。
Wordleは5文字の英単語を当てるゲームです。
毎日0時に、その日の単語が更新されます。みんなで同じ単語を解くことになるので、何が出たとかはネタバレになります。
最初は英和辞書検索が便利で、色々やってたんですが、効率化したくなってしまったのでPythonで書きました。
効率的な英単語
誰でも思いつくと思いますが、英単語に頻出するアルファベットを使った単語から攻めていくのが良いです。
eが最も多くてqとかzが少ないみたいな話はシーザー暗号で有名ですね。
何を最初に入力するのが一番良いのかは諸説ですが、ariseなんかは母音やr,sが絞れて良さそうです。
英単語を/usr/share/dict/wordsから引っ張ってきて、小文字5文字の単語を抽出します。
cat /usr/share/dict/words |grep -E "^[a-z]{5}$" > word_dict.txt
Wordleが同じ語彙を使っているかは不明です。
with open('word_dict.txt') as f:
word_list = f.read().splitlines()
# 26文字取得
alphabets = [chr(ord("a")+i) for i in range(26)]
# 全部マージ
word_merged = ''.join(word_list)
alph_cnt = {c: word_merged.count(c) for c in alphabets}
ソートすると
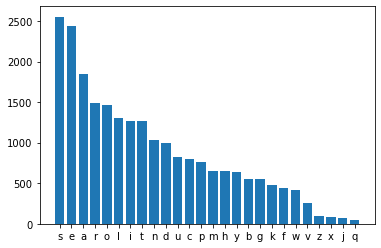
sが多いですが、5文字縛りだとこれは多分三人称単数とか複数形の寄与が大きいとかそういうのではないでしょうか。
正規表現で解く
このような画像の状態では

どういう単語を入れるべき(入れるべきでない)でしょうか?
streの4文字は確定で入らないですし、各ポジションではr,pi,rp,i,が入りそうにないです。
つまり、頭の悪い正規表現を書くと、^[^(r)^(stre)][^(pi)^(stre)][^(rp)^(stre)][^(i)^(stre)][^(stre)]$が探すべき文字列です
import re
re_ptn = re.compile('^[^(r)^(stre)][^(pi)^(stre)][^(rp)^(stre)][^(i)^(stre)][^(stre)]$')
[word for word in words if ptn.search(word) is not None]
# ['abaci', 'aback', 'abaft', 'abase', 'abash', ...]
これで必ず入れてはいけない単語は篩にかけられましたが、rpiの3つが入ってる単語がほしいですね。
[word for word in words if all([c in word for c in 'rpi']) and ptn.search(word) is not None][:10]
# ['carpi', 'chirp', 'crimp', 'crisp', 'drips', ...]
あとはコードを書くだけです。
基本的には頻出文字から順に正規表現で検索する文字を増やす、ただし入れてはいけない単語は除外するという方針を取ると良さそうです。
コードの公開はしませんがここまで書けば実装できると思います。
やってみよう
自分で作ったwordleもどきで試しました。
1手目ではaroseという単語が出てきました。今回使ってる単語群の中ではこれが最も効率の良い単語みたいです。
2手目ではisletかuntilが候補として出てきました。
既にわかっている情報を全て活用する「当てに行く」と、2手目で当てることを諦めて、使用される単語を「絞る」の2パターンがあります。
1手目で3文字当ててしまった状態で当てに行こうとすると、1手順あたり2文字しか探索できないので、候補数との兼ね合いで決めるとよさそうです。
3手目までは当てに行って、4手目では残りの1文字に対して候補が6通りあったため、絞る方針を取りました。
絞る選択肢の実装は適当です。この場合の最善手はwovenだと思います。
色々雑なのでもっといいやり方もあるかもしれません。
ちなみに全ての手順で当てに行く戦略をとったときの解答までの平均手順数は4.37(回数制限無し)らしいです(単語数4594)。
回数制限無しで探索したときの手数の分布
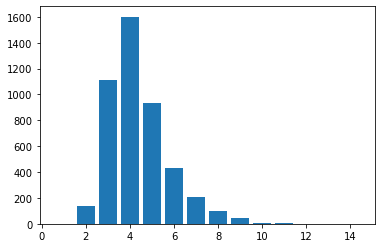
8割は6手順以内に解けるらしい(3780/4594)。
いかがでしたか?
結論:どう考えても自分で考えて解くほうが楽しい