13日目: BinaryIndexedTreeを実装する

競プロ用ライブラリを作る Advent Calendar 2024の13日目です.

BinaryIndexedTreeって?

Fenwick Treeとも呼ばれます.

SegmentTreeに制限を付けてデータを減らして定数倍を軽くしたものです.

仕組み

普通のセグ木はこういう風に区間の情報を管理します.

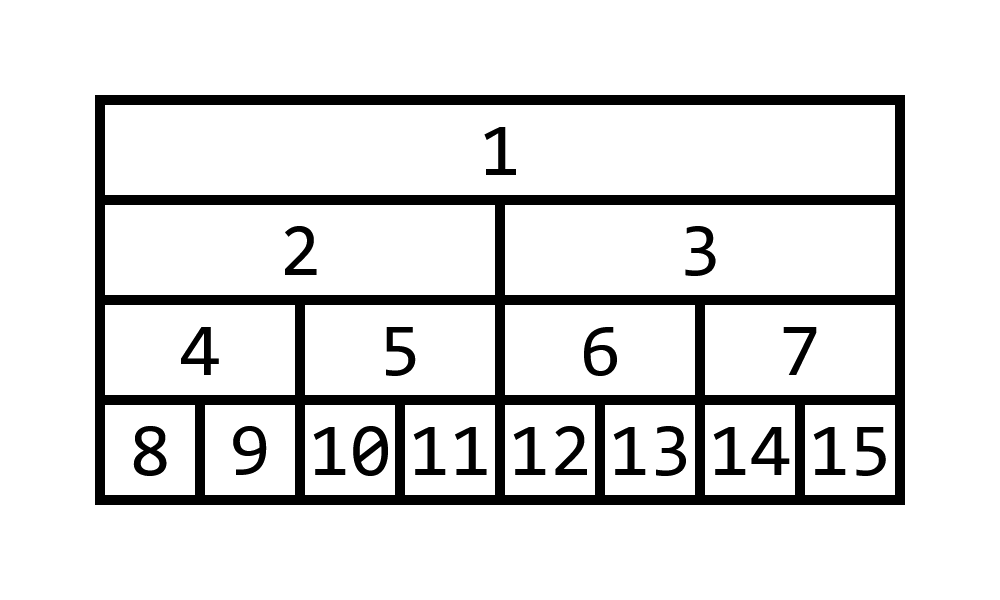
でも, 列の先頭から始まる区間のクエリしか与えられないなら, 使う区間の数は減らせますね.

$x_1, x_2, ..., x_N$という列のBinaryIndexedTreeの各要素$y_k$は$[k+1-2^{\operatorname{trailing}(k)},k]$の区間の情報を持つことにします. ここで$\operatorname{trailing}(k)$は$k$を2進法で表記したときの末尾の連続した1の個数を表します. 偶数なら0で, 奇数なら1以上ですね.

これで値の更新をするためにはSegmentTreeのモノイドという条件に加えてさらに幾つか制約が付いてきます.
アーベル群が乗るんですが, ここでは具体例として

・列の指定した要素の数を増減させる
・指定した区間の和を求める

というクエリの場合を考えます.

struct SampleBIT {}

指定した要素の数を増減させる

その要素が含まれる区間を全て同じ量増減させればいいです.

どうすればいいかというと, 2進法で書いた時の一番下の0を1にする操作を繰り返せばいいです.
足し算の繰り上がりを使えばi |= (i+1) & ~iという操作でこれを実現できます.

impl SampleBIT {
    fn add(&mut self, mut index: usize, val: i32) {
        while index < self.data.len() {
            self.data[index] += val;
            // Rustではビット反転は「~」ではなく「!」です
            index |= (index + 1) & !index;
        }
    }
}

指定した区間の和を求める

例えば区間$[l, r)$の和を求めるには区間$[0, r)$の和から区間$[0, l)$の和を引けばいいです.
という訳で区間の左端が$0$の場合だけを考えます.

閉区間で情報を持っているのでそれに気を付けると, $[0, r)$の区間には$y_{r-1}$が持っている区間を含んでいます. なので結果は$y_{r-1} + $「$[0,r-2^{\operatorname{trailing}(r-1)})$の区間和」です
2進数表記と見比べることで, $r-2^{\operatorname{trailing}(r-1)}$はr - (r & ~(r-1))みたいに計算できることが分かります.

impl SampleBIT {
    fn sum(&mut self, mut index: usize) -> i32 {
        let mut sum = 0;
        while index > 0 {
            sum += self.data[index - 1];
            index -= index & !(index - 1);
        }
        sum
    }
}

実装

• binaryindexedtree.rs
  抽象化もアーベル群くらい緩いのでやりやすいです.

まとめ

いかがでしたか?

明日は便利だけど思ったより使用頻度が低いやつを実装します.