11日目: SegmentTreeを実装する

競プロ用ライブラリを作る Advent Calendar 2024の11日目です.

SegmentTreeって?

長さ$N$の列が与えられたとき

• 指定した区間の最小値だったり和だったりを$O(\log N)$で求める
• 列のある1つの値を$O(\log N)$で書き換える

ということができるデータ構造です.

「最小値だったり和だったり」は正確にはモノイドというもので, 2項演算$x\ast y$ (最小値だったら$x\ast y=\min(x,y)$だし, 和だったら$x\ast y=x+y$) が以下の性質を満たしていればなんでもいけます.

• 任意の$x, y, z$ について $(x\ast y)\ast z = x\ast(y\ast z)$
• 「任意の$x$について$x\ast e = e\ast x=x$」を満たす$e$が存在する

つまり群の逆元が無くてもいいバージョンです.

仕組み

ある程度の, 更新のコストもかかりすぎないくらいの量の区間について事前に計算しておいて, その情報を組み合わせることで高速にクエリに答えます.
列の長さを2の冪にそろえてやる方法が有名です. 下の図のように前計算の区間をまとめます.

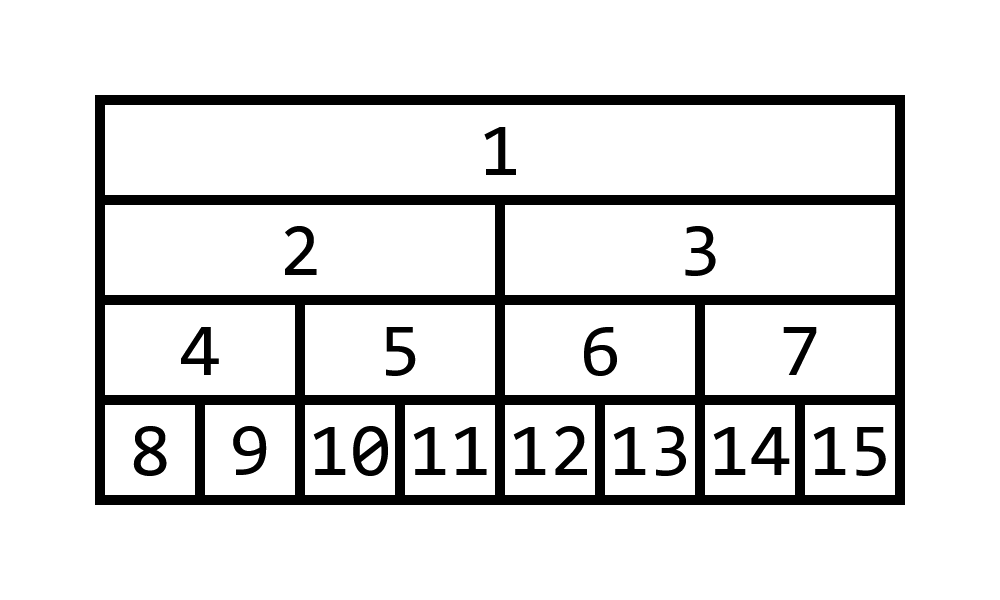
例えば9のところから14のところまでの区間の値を計算するには9番, 5番, 6番, 14番の情報を組み合わせればいいです.

ここでは2の冪に揃えなくてもよい実装をしてみます. 下の図のようなことをしてみます.

最早木ではないのでSegmentForestとでも呼んだ方が正しそうですが, SegmentTreeとあまり変わらない上にその名前が浸透しすぎてるのでそう呼ぶことにします.

長さ$N$の列をSegmentTreeにすると$N$個の要素からなる層, $\lfloor\frac{N}{2}\rfloor$個の要素からなる層, $\lfloor\frac{N}{4}\rfloor$個の要素からなる層... が出来ます.

一番下の$N$個の要素からなる層は元の列の情報をそのまま持ちますね. 図では0番~6番のところのことです.
より上の層は, 左から$x$番目の要素は1つ下層の$2x-1$番目の要素と$2x$番目の要素を組み合わせている, とします.

サンプルコードではこれを二次元配列で表現しますが, 実際の実装では1つの配列で表現しました.

// サンプルコードではi32の足し算を扱うセグ木を実装します
struct SampleSegTree {
    data: Vec<Vec<i32>>,
    len: usize,
}

impl SampleSegTree {
    fn new(len: usize) -> Self {
        let mut data = vec![];
        for i in 0.. {
            if len >> i == 0 {
                break;
            }
            data.push(vec![0; len >> i]);
        }
        Self { data, len }
    }
}

値の更新は, 一番下の層を更新し, その影響を受ける上の層の情報を更新します.

impl SampleSegTree {
    fn set(&mut self, index: usize, val: i32) {
        // 一番下の層の値をセットする
        self.data[0][index] = val;
        // より上の層を更新する
        for i in 1..self.data.len() {
            // その層でのインデックスを調べる
            let idx = index >> i;
            // その層の管轄外 (上の図の6番みたいなこと) なら終了させる
            if idx >= self.data[i].len() {
                break;
            }
            // 各層のidx番目の要素は1つ下の層の2*idx-1番目の要素と2*idx番目の要素をまとめてる
            // 配列の添え字は0から始まるので説明とプログラムで式が少し違います
            self.data[i][idx] = self.data[i - 1][idx * 2] + self.data[i - 1][idx * 2 + 1];
        }
    }
}

区間の和を計算する関数も実装しましょう. どう効率的に情報を選ぶかですが, これは消去法で考えると上手くいきます.
「左から$x$番目の要素は1つ下層の$2x-1$番目の要素と$2x$番目の要素を組み合わせている」なので, $2x$番目の要素が左端にくるような区間や$2x-1$番目の要素が左端にくるような区間はより上の層にはないです.

逆にそうでなければ上の層に要素があるので上の層から情報をとる, という風にします. 私はこれをac-libraryのコードを写経して理解しました.

impl SampleSegTree {
    // 区間 [left, right) の和を計算する (区間にrightは含まないことに注意)
    fn sum(&self, mut left: usize, mut right: usize) -> i32 {
        let mut sum = 0;
        for layer in self.data.iter() {
            // インデックスが奇数の要素が左の境界になる区間はより上の層にはない
            if left % 2 == 1 {
                sum += layer[left];
                left += 1;
            }
            // インデックスが奇数の要素が右の境界になる区間はより上の層にはない
            if right % 2 == 1 {
                right -= 1;
                sum += layer[right];
            }
            // 残りの要素が無くなったらその時点での和を返す
            if left == right {
                return sum;
            }
            // 1つ上の区間での区間の境界はこう計算できる
            left /= 2;
            right /= 2;
        }
        // 一番上の層は要素が1つしかないので, そこで必ず要素は無くなります.
        // そのため, 上にあるreturnで関数が終了され, ここに到達することはありません.
        unreachable!();
    }
}

実装

• segmenttree.rs

そのデストラクタで更新を行う, 要素の可変参照のラッパーも作りました. 更新が行われるまで他の操作を型システムで禁止できるのは所有権システムの勝利ですね.

まとめ

いかがでしたか?

明日は定数時間でクエリを処理できるやつを作ります.