Pytorchの自動微分を使ってハミルトン形式の力学計算

環境

• OS: Windows 10 Home
• CPU: Inten Core i9-9900KF
• RAM: 16.0 GB
• GPU: Geforce RTX 2070 SUPER
• VRAM: 8.0 GB
• Python 3.8.2
• Pytorch 1.9.0+cu111
• CUDA 11.1

目的

　以前の記事に誤りを見つけてそのまま直すのもしんどかったので、拡張性を持つように工夫してコードを書き直しました。さらにニュートン方程式で力のベクトルの向きを考えるのもミスの要因になるので、今回はベクトルを考えなくて済むハミルトン形式に挑戦しました。

問題設計

　実際に解く系は以前の記事と同じとして解析力学で表現するお膳立てをします。

ニュートン方程式

　みなさんご存知、ニュートンの運動方程式は$m\overrightarrow{a} = \overrightarrow{F}$ですね。ベクトルで書いてしまうとなんてことありませんが、こいつを数値的に解こうとすると$\overrightarrow{F}$を$x, y$や$r, \theta$などの方向に分解する必要があります。具体的には例えばバネ定数$k$、自然長$l$のバネで結ばれた質点の位置を$\overrightarrow{r_1} = (x_1, y_1)^T, \overrightarrow{r_2} = (x_2, y_2)^T$としたニュートン方程式は次の通りです。

\left\{
\begin{align}
m\frac{d^2 \overrightarrow{r_1}}{d t^2} &= -k(|\overrightarrow{r_1} - \overrightarrow{r_2} | - l)\frac{\overrightarrow{r_1} - \overrightarrow{r_2}}{|\overrightarrow{r_1} - \overrightarrow{r_2}|}\\
m\frac{d^2 \overrightarrow{r_2}}{d t^2} &= -k(|\overrightarrow{r_1} - \overrightarrow{r_2} | - l)\frac{\overrightarrow{r_2} - \overrightarrow{r_1}}{|\overrightarrow{r_1} - \overrightarrow{r_2}|}\end{align}
\right.

この右辺をPytorchで書くと次のようになります。

newton.py

import torch

def F(r1, r2, k=1.0, l=1.0):
    R = torch.sqrt(((r1-r2)**2).sum())
    f1 = -k*(R - l)*(r1 - r2)/R
    f2 = -k*(R - l)*(r2 - r1)/R
    return f1, f2

　さてここで負号を忘れたりr1, r2の順番を逆にしたりすると間違った結果が出力されてしまいます。なぜそんなことが起こるかといえばベクトルには向きがあるからです。じゃあどうすればそんなミスを防げるのか。例えばスカラーには向きがないことから、スカラーで表現すれば良いと想像できます。動機は朋花くそんな表現体系になっているのが解析力学です。解析力学ではデカルト座標や曲座標でも同じ形の式が使えます。また解析力学の式はニュートン方程式と同値なことが証明されています（物理法則がいくつもあるはずがない）。私は合成化学出身の材料技術者なので正確な理論の話は他に任せる¹²³として、以下では天下り的に解析力学を使っていきます。

正準方程式

　頭のいい方々によると物体の座標$q$とそれに対応した運動量$p$の時間微分はハミルトニアン$H(t, q, p)$を用いて次のようになります。

\left\{
\begin{align}
\frac{dq}{dt} &= \frac{\partial}{\partial p}H(t, q, p) \\
\frac{dp}{dt} &= -\frac{\partial}{\partial q}H(t, q, p)
\end{align}
\right.

これが正準方程式と呼ばれます。ポテンシャル$V(q)$を持ち、非保存力がなく運動量もしくは速度に依存した力もない（もしくは運動エネルギー$K$が$p^2/2m$と表される）場合のハミルトニアンは$H = p^2/{2m} + V(q)$となるので、これを上の正準方程式に代入すると次のようになります。

\left\{
\begin{align}
\frac{dq}{dt} &= p/m\\
\frac{dp}{dt} &= -\frac{\partial V}{\partial q}
\end{align}
\right.

非保存力$F$があるならおそらく非保存力がある場合のラグランジュの運動方程式をルジャンドル変換して$dp/dt = -\partial V/{\partial q} + F$となるはずです（ニュートン方程式と同値ならこうなるはず）。真っ当な数値計算であればさらに$-\partial V/\partial q$を変数$t, q, p$で表しますが、面倒臭がりでしょっちゅう計算ミスする私はこの偏微分計算をPytorchの自動微分に丸投げしてしまいたいというのが本記事の主題です。

Pytorchでの表現

　というわけで系全体の運動エネルギー$K$、ポテンシャル$V$、そしてミルトニアン$H$さえ計算できれば、自動微分の力を借りて正準方程式から時間微分を計算し、任意の時間発展アルゴリズムを適用するだけです。なお個々の粒子のハミルトニアンを積み重ねた列ベクトルではなく系全体のハミルトニアンとする主な理由はPytorchの自動微分torch.autogradで微分する対象はスカラーでなければならないからです。
　注意点として微分して$d\sqrt{x}/dx = 1/\sqrt{x}$となる部分があった場合、$x=0$が代入されるとtorch.autogradはnanを返します。バネで結ばれた複数粒子のポテンシャルを行列で表現して計算すると対角成分がまさにこれに該当します。これを回避するために以下のコードでは2乗根をとる前に対角成分に1を足しています。該当する要素は$(x_i - x_i)^2$の関数であり微分すると$x_i - x_i$を積に含むため、導係数は必ず0となり計算上の支障はありません。

field.py

import torch

class Potential:
    def kinetic_energy(self, t, q, p):
        k = (p**2/2/self.m).sum()
        return k

    def hamiltonian(self, t, q, p):
        k = self.kinetic_energy(t, q, p)
        v = self.potential_energy(t, q, p)
        return k + v


class Harmonic(Potential):
    def __init__(self, m, l, k):
        self.m = m
        self.k = k
        #粒子間の相互作用を記述したクラスを適宜同時に継承すること
        #self.k_ = self.set_connectivity(k)
        self.l = l

    def potential_energy(self, t, q, p):
        r = ((q.reshape(self.dim, -1, 1)
                -q.reshape(self.dim, 1, -1))
            **2).sum(dim=0)
        # diff sqrt(x)|x=0 causes Error
        # and torch returns nan
        r = (r + torch.eye(r.shape[0], device=self.device)).sqrt()
        V = ((1/2*self.k*(r - self.l)**2)/2).sum()
        return V


class LJ(Potential):
    def __init__(self, m, e, s, p=12, q=6):
        self.m = m
        self.e = e
        self.s = s
        #self.e_ = self.set_connectivity(e)
        #self.s_ = self.set_connectivity(s)
        self.p = p
        self.q = q

    def potential_energy(self, t, q, p):
        xi = q.reshape(3, -1, 1)
        xj = q.reshape(3, 1, -1)
        r = ((xi-xj)**2).sum(dim=0)
        r = (r + torch.eye(r.shape[0],device=self.device)).sqrt()
        v = (4*self.e*((self.s/r)**self.p - (self.s/r)**self.q)
                ).sum()/2
        return v


class Morse(Potential):
    def __init__(self, m, d, a, l):
        self.m = m
        self.d = self.set_connectivity(d)
        self.a = self.set_connectivity(a)
        self.l = self.set_connectivity(l)

    def potential_energy(self, t, q, p):
        xi = q.reshape(3, -1, 1)
        xj = q.reshape(3, 1, -1)

        r = ((xi-xj)**2).sum(dim=0)
        r = (r + torch.eye(r.shape[0],device=self.device)).sqrt()
        v = (self.d
                *(1 - torch.exp(-self.a*(r - self.l)))**2
            ).sum()/2
        return v

　調子に乗ってLJポテンシャルやモースポテンシャルも作りましたが動作確認は全く行なってません。これらポテンシャルを用いて実際に正準方程式を計算するには一緒に次のclass Hamiltonianを継承したクラスをmain.pyで定義します。

hamiltonian.py

import torch

def requires_grad(func):
    def wrapper(self, t, q, p, **kwargs):
        q.requires_grad = True
        q.grad = None
        p.requires_grad = True
        p.grad = None
        return func(self, t, q, p, **kwargs)
    return wrapper

class Hamiltonian:
    def __call__(self, t, q, p):
        return self.hamiltonian(t, q, p)

    @requires_grad
    def dqdt(self, t, q, p):
        h = self.hamiltonian(t, q, p)
        g = torch.autograd.grad(h, p)
        return g[0]

    @requires_grad
    def dpdt(self, t, q, p):
        h = self.hamiltonian(t, q, p)
        g = torch.autograd.grad(h, q)
        return -g[0]

    @requires_grad
    def gradient(self, t, q, p):
        h = self.hamiltonian(t, q, p)
        h.backward()
        return torch.stack([p.grad, -q.grad])

　また格子点を生成するのに便利なclass Latticeも作っておきます。

points_design.py

import torch
import numpy as np


class Lattice:
    def __init__(self, N, l, device='cpu'):
        '''
        Base class of lattice.

        Parameters
        ----------
        N: Number(s) of point(s), int or array(int,)
        l: distance between points, float or array(float,)
        '''
        self.N = N
        self.Nx = self.Ny = self.Nz = 1
        if type(self.N) is int:
            self.Nx = self.N
            self.dim = 1
        elif len(self.N) == 3:
            self.Nx, self.Ny, self.Nz = self.N
            self.dim = 3
        elif len(self.N) == 2:
            self.Nx, self.Ny = self.N
            self.dim = 2
        elif len(self.N) == 1:
            self.Nx, = self.N
            self.dim = 1
 
        self.l = l
        self.device = device

    def set_connectivity(self, *args):
        Nx = Ny = Nz = 1
        if type(self.N) is int:
            Nx = self.N

        elif len(self.N) == 3:
            Nx, Ny, Nz = self.N
        elif len(self.N) == 2:
            Nx, Ny = self.N
        elif len(self.N) == 1:
            Nx, = self.N

        if len(args) == 3:
            kx, ky, kz = args
        else:
            kx = ky = kz = args[0]
        items = Nz*Ny*Nx
        E = torch.eye(items,
                      device=self.device,
                      dtype=torch.float64)
        c = [[0, None, None, -(Nx*Ny), kz],
             [-1, None, None, Nx*Ny, kz],
             [torch.arange(Nz), 0, None, -Nx, ky],
             [torch.arange(Nz), -1, None, Nx, ky],
             [torch.arange(Nz), torch.arange(Ny), 0, -1, kx],
             [torch.arange(Nz), torch.arange(Ny), -1, 1, kx]
             ]
        C = torch.zeros_like(E)
        for i, j, k, roll, kk in c:
            I = torch.ones(Nz, Ny, Nx,
                           device=self.device,
                           dtype=torch.float64)
            I[i, j, k] = 0.
            I = I.reshape(-1,1)*kk
            C += torch.roll(E*I, roll, dims=1)

        return C

    def set_points(self):
        device = self.device
        lx = ly = lz = 1.
        if type(self.l) is float:
            lx = self.l
        elif len(self.l) == 3:
            lx, ly, lz = self.l
        elif len(self.l) == 2:
            lx, ly = self.l
        elif len(self.l) == 1:
            lx, = self.l

        Nx = Ny = Nz = 1
        if type(self.N) is int:
            Nx = self.N
            x = torch.arange(0,Nx,
                             dtype=torch.float64,
                             device=device)*lx
        elif len(self.N) == 3:
            Nx, Ny, Nz = self.N
            x = torch.arange(0,Nx,
                             dtype=torch.float64,
                             device=device)*lx
            y = torch.arange(Ny-1,-1,-1,
                             dtype=torch.float64,
                             device=device)*ly
            z = torch.arange(Nz-1,-1,-1,
                             dtype=torch.float64,
                             device=device)*lz
            x, y, z = torch.meshgrid(x, y, z)
            x = torch.stack([x.T, y.T, z.T])
        elif len(self.N) == 2:
            Nx, Ny = self.N
            x = torch.arange(0,Nx,
                             dtype=torch.float64,
                             device=device)*lx
            y = torch.arange(Ny-1,-1,-1,
                             dtype=torch.float64,
                             device=device)*ly
        elif len(self.N) == 1:
            Nx, = self.N
            x = torch.arange(0,Nx,
                             dtype=torch.float64,
                             device=device)*lx

        v = torch.zeros_like(x)

        return x, v

　これで物理的情報は全て記述できたので次は時間発展アルゴリズムの実装です。以前のミスってる記事では4次のルンゲクッタ法のみでしたが、今回は速度ベルレ法と特殊なオイラー法も実装します。ただしオイラー法はコードしただけで力尽きて動作確認してません。追加した2つはルンゲクッタ法と比べてSymplectic性¹⁴という性質によってハミルトニアン（=エネルギー）が保存されやすいそうで、計算量とコード量も少なく済みます。
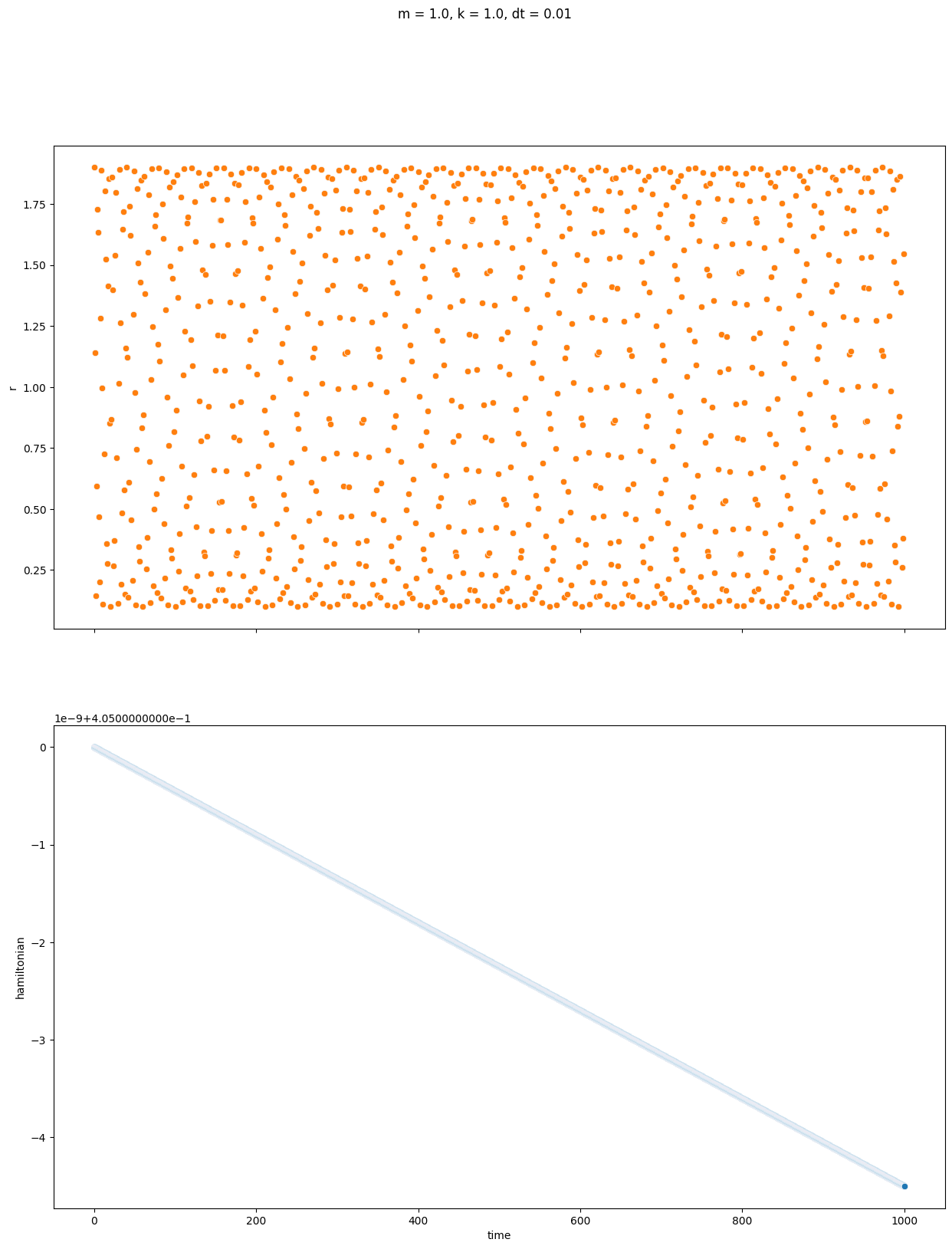
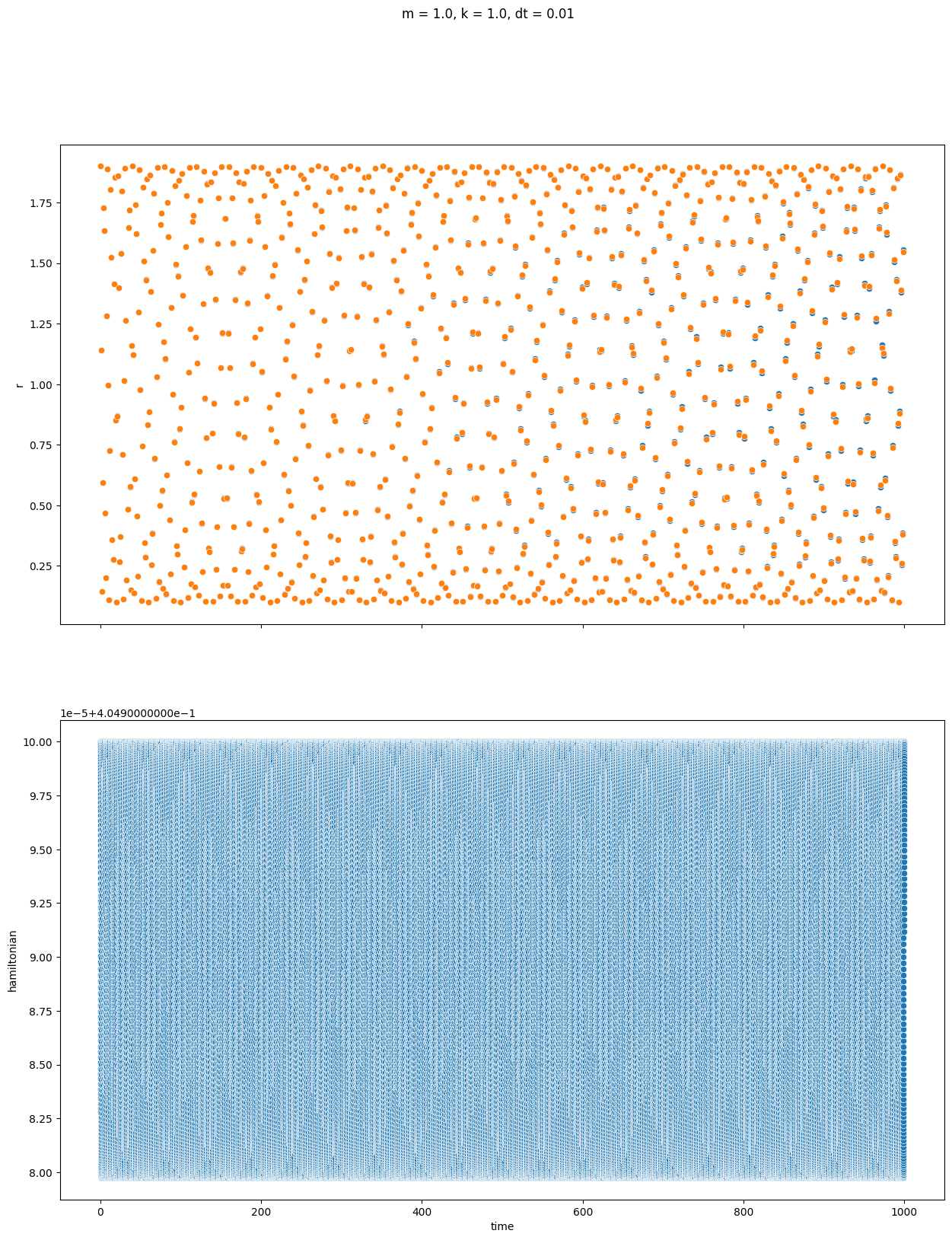
　が、今回のバネで繋いだ格子点の運動では速度ベルレ法よりルンゲクッタ法の方がエネルギーが安定していました。~~またミスってるのか？~~詳細は後述しますが、解析的に解ける2粒子系の運動で0.01秒刻みで1000秒まで試すと速度ベルレ法の全エネルギーが(4.0499±0.0001)e-1の間で振動していたのに対して、ルンゲクッタ法は4.05e-1から4.5e-9だけ単調減少しました。

solver.py

from pathlib import Path
from datetime import datetime
import numpy as np
import torch


class Solver(object):
    def __init__(self, t0, dt, dydt, *args,
            set_boundary=None, wd=None,
            fps=15, cashe=False):
        '''
        Parameters
        ----------
        dydt: Python function
        t0: start time
        dt: time step
        args: parameters for dydt
        '''
        self.t = t0
        self.dt = dt
        self.dydt = dydt
        self.args = args
        self.results = {'t':[t0], 'args':{}}
        # 保存タイミングを制御するためにリストで保持させたけど
        # メモリ不足で活用できそうになかった
        for i in range(len(args)):
            self.results['args'][i] = [args[i].detach().to('cpu')]

        if wd is None:
            self.wd = Path.cwd()
        else:
            self.wd = wd

        self.fps = fps
        self.cashe = cashe

    def step(self):
        steps = self.alg()
        for y, s in zip(self.args, steps):
            y.data += s
        self.t += self.dt
        self._to_results()

        return self.t

    def _to_results(self):
        self.results['t'].append(self.t)
        for i in range(len(self.args)):
            self.results['args'][i].append(
                   self.args[i].detach().to('cpu')
                )

     def save(self):
        t = np.array(self.results['t'])
        with open(self.wd/'result_time.csv', 'ab') as f:
            np.savetxt(f, t)
        self.results['t'] = []

        for i in range(len(self.args)):
            with open(self.wd/f'results_args_{i}.csv', 'ab') as f:
                arg = torch.stack(
                        self.results['args'][i]
                    ).detach().reshape(1,-1).to('cpu').numpy()
                np.savetxt(f, arg)
            self.results['args'][i] = []


class RungeKutta(Solver):
    def alg(self):
        dydt = self.dydt
        t = self.t
        param = self.args
        k1 = dydt(t, *param)

        t = self.t + self.dt/2
        param = [a.detach() + self.dt/2*k
                    for a, k in zip(self.args, k1)]
        k2 = dydt(t, *param)

        t = self.t + self.dt/2
        param = [a.detach() + self.dt/2*k
                    for a, k in zip(self.args, k2)]
        k3 = dydt(t, *param)

        t = self.t + self.dt
        param = [a.detach() + self.dt*k
                    for a, k in zip(self.args, k3)]
        k4 = dydt(t, *param)

        return self.dt/6*(k1 + 2*k2 + 2*k3 + k4)


class VelocityVerlet(Solver):
    def step(self):
        a = self.dydt
        x = self.args[0]
        v = self.args[1]
        t = self.t
        dt = self.dt
        at = a(t, *self.args)
        self.args[0].data += v*dt + at/2*dt**2

        t += dt
        self.args[1].data += (at + a(t,*self.args))/2*dt
        self.t = t

        self._to_results()

        return self.t


class SymplecticEuler(Solver):
    def step(self):
        self.args[1].data += self.dydt(self.t,*self.args)*self.dt
        self.args[0].data += self.args[1]*self.dt
        self.t += self.dt

        self.results['t'].append(self.t)
        self.results['args'].append(self.args)

        self._to_results()

        return self.t

　長々とお膳立てしてやっと本体。ポテンシャルとハミルトニアンと粒子の配置を継承させて座標変換を定義して系を完成させてSolverで解く。

main.py

from pathlib import Path
import os
from datetime import datetime

import numpy as np
import torch
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns

from field import Harmonic
from hamiltonian import Hamiltonian
from points_design import Lattice
from solver import RungeKutta, VelocityVerlet


class LatticeHarmonic(Lattice, Harmonic, Hamiltonian):
    def __init__(self, m, N, l, k, device):
        Lattice.__init__(self, N, l, device)
        Harmonic.__init__(self, m, l, k)

    @staticmethod
    def x2q(t, x, v):
        return t, x, v

    @staticmethod
    def q2x(t, q, v):
        return t, q, v

    def v2p(self, t, q, v):
        return t, q, self.m*v

    def p2v(self, t, q, p):
        return t, q, p/self.m

    def cart2gen(self, t, x, v):
        t_, q, v_ = self.x2q(t, x, v)
        t_, q, p = self.v2p(t, q, v)
        return t, q, p

    def gen2cart(self, t, q, p):
        t_, q, v = self.p2v(t, q, p)
        t_, x, v = self.q2x(t, q, v)
        return t, x, v


def test_RK(m=1., N=2, l=1., k=1., dt=1.e-2, te=10.):
    device = torch.device(
                    'cuda:0' if torch.cuda.is_available()
                    else 'cpu')

    lattice = LatticeHarmonic(m, N, l, k, device)
    x, v = lattice.set_points()
    if lattice.Nz == lattice.Ny == 1:
        x[-1] *= 1.9
    elif lattice.Nz == 1:
        x[0, -1, -1] *=1.9
    else:
        x[0, -1, -1, -1] *= 1.9
    t = t0 = 0.
    t, q, p = lattice.cart2gen(t, x, v)
    Nx = Ny = Nz = 1
    if type(N) is int:
        Nx = N
    elif len(N) == 2:
        Nx, Ny = N
    elif len(N) == 3:
        Nx, Ny, Nz = N

    wd = Path.cwd()/'loop'/'RK4'/f'm{m}_Nx{Nx}_Ny{Ny}_Nz{Nz}_l{l}_k{k}_{datetime.now():%Y%m%d%H%M}'
    wd.mkdir(parents=True)
    solver = RungeKutta(
                t0, dt, lattice.gradient, q, p, wd=wd
                )
    h = []

    with torch.no_grad():
        h.append(lattice(t, q, p))

    solver.save()
    h = (torch.stack(h).detach()
         .reshape(1,-1).to('cpu').numpy()
        )
    with open(wd/'result_h.csv', 'ab') as f:
        np.savetxt(f, h)
    h = []

    while t < te:
        t = solver.step()
        q = solver.args[0]
        p = solver.args[1]
        h.append(lattice(t, q, p))

        # 1/freqの頻度で保存
        if int((t-t0)/dt)%freq == 0:
            solver.save()
            h = (torch.stack(h).detach()
                 .reshape(1,-1).to('cpu').numpy()
            with open(wd/'result_h.csv', 'ab') as f:
                np.savetxt(f, h)
            h = []

    return wd

if __name__=='__main__':
    test_RK()

　そろそろかなり記事が長くなってしまっているので速度ベルレ法の実行関数は省略しましたが、a = lambda t,q,p: lattice.dpdt(t,q,p)/mをsolver.VelocityVerletに与えればルンゲクッタ法と同じです。

解析解との差

　上記をバネで繋いだ2粒子に対して実行して解析解とのズレと全エネルギーの変動を見たのが次です。1000秒間を0.01秒刻みで全て描画しようものなら本体の計算より遥かに時間がかかって終わらないため、描画は1秒刻みに間引きました。~~お前高速とか言ってPyQtgraphの記事書いてるなら使えよ。~~2粒子間の距離を上、エネルギーを下の行にそれぞれプロットしています。重なっているので分かりにくいですが、青点が数値計算、橙点が解析解を表しています。

まずルンゲクッタ法

次に速度ベルレ法

　ある範囲内に収まるという意味では確かに速度ベルレ法の方が安定していますが、誤差という意味では1e8秒くらいまで計算しない限りはルンゲクッタ法の方が正確でした。

1. 数値計算のための解析力学, 神戸大学　陰山 聡 ↩ ↩²

2. 物理のかぎしっぽ ↩

3. EMANの解析力学 ↩

4. 数値解析と物理学
   　 ↩