Go to Qiita Advent Calendar 2024 Top
LoginSignup
5
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

MATLAB/SimulinkAdvent Calendar 2024

Day 13
@Yuki_MATLAB_Amb(ゆうきち)

MATLABで使える進化計算ライブラリPlatEMOの紹介（とエネルギー法による倒立振子の振り上げ）

Last updated at Posted at 2024-12-12

この記事はMATLAB/SIMULINK Advent Calendar 2024の13日目の記事です！
13日の金曜日:thinking::thinking::thinking:

間違ってるところがあれば教えてください。。。

最適化

最適化とは、ある制約の下で目的関数を最小（最大）化することです。
1目的の最大化問題はこんなやつ

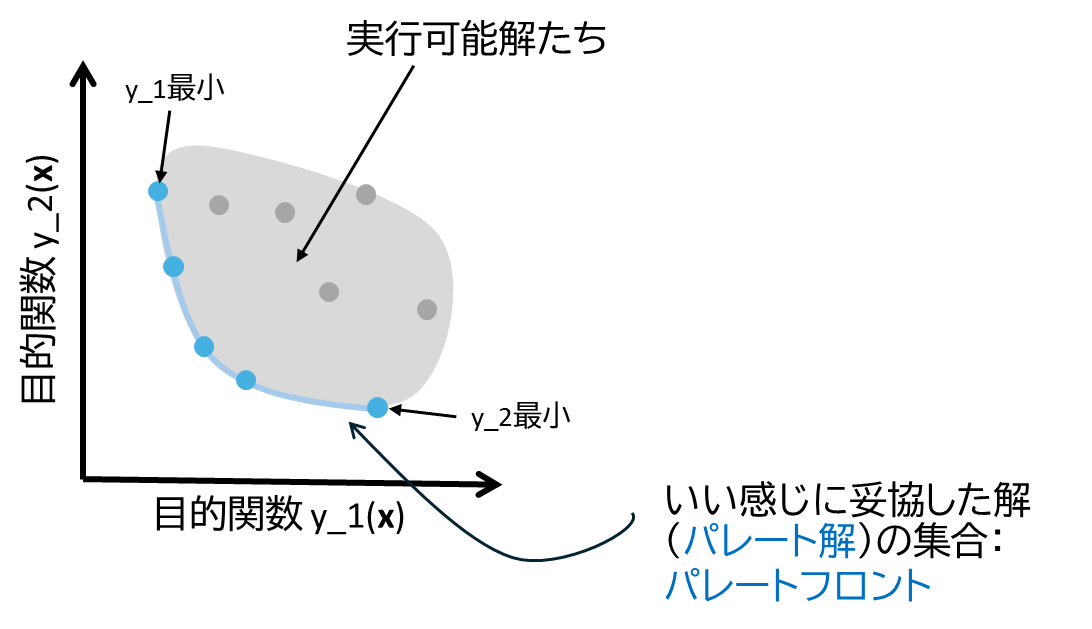
2目的の最小化問題はこんなやつですね。

進化計算

遺伝的アルゴリズムとは

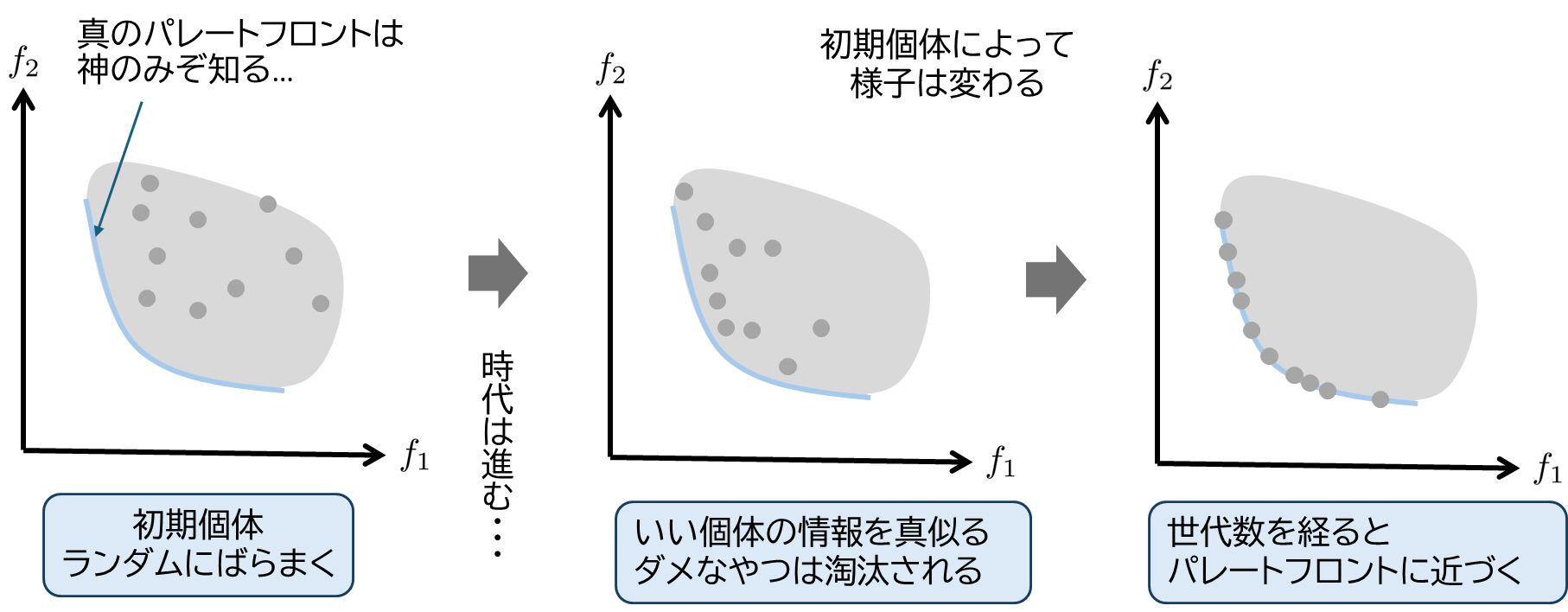
2目的の最小化問題を考えます。
最初は、変数$\boldsymbol{x}$を適当な値で何パターンか計算してみます。

image.png

この初期個体たちは目的関数空間に散らばっていますが、最小化問題であれば左下にいる個体の方が偉く、右上にいる個体は成績の悪いダメなやつらということになります。

そして次の世代では、成績の良い個体が生き残り子孫を残し（特徴を受け継ぐ）、ダメなやつらは淘汰されます。
これを繰り返すことによって、だんだんと成績が良くなっていき、最適解へと近づいていきます。

局所解に陥らないように突然変異させたりというのもありますが、詳しくはググってください()

PlatEMOとは

概要

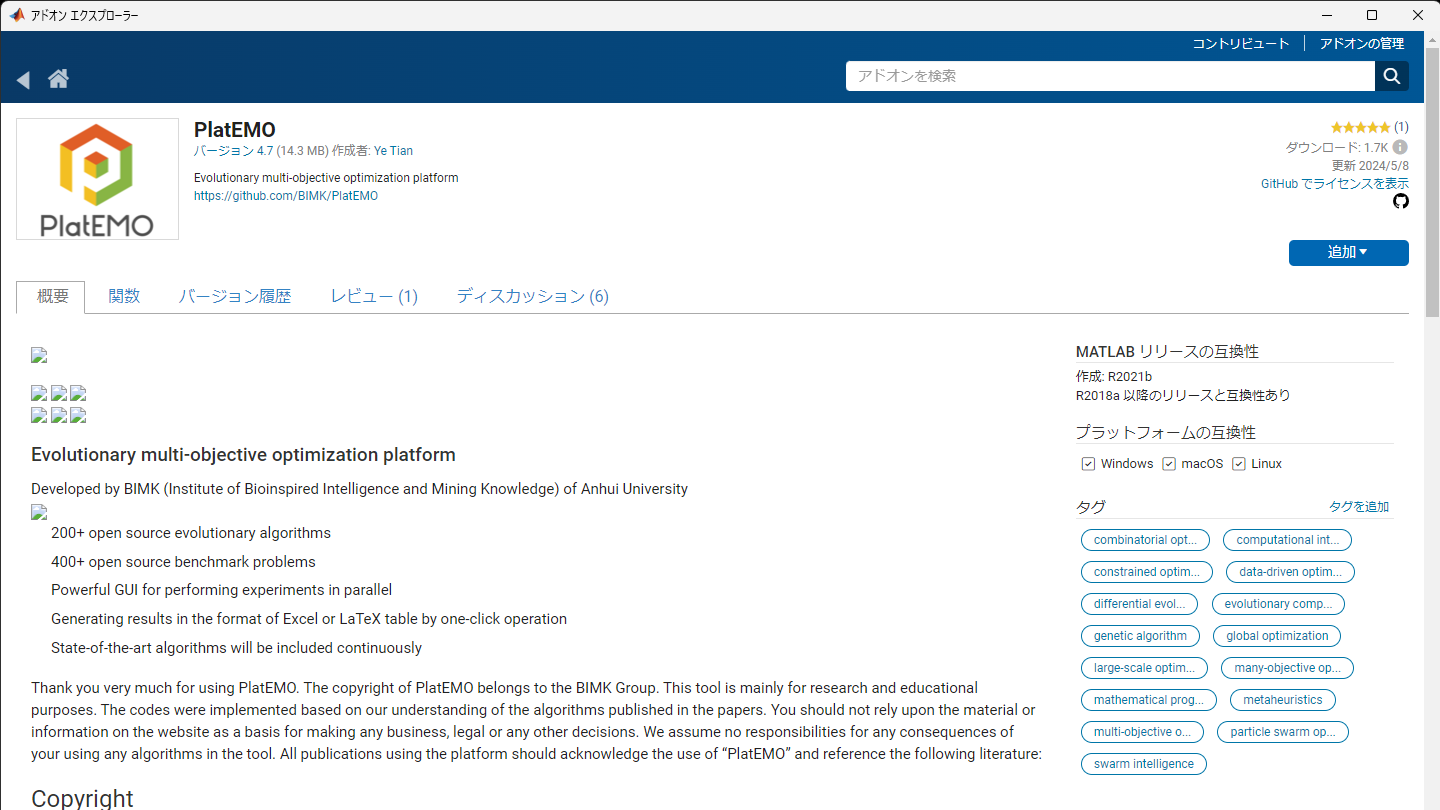
PlatEMOは安徽大学のBIMK (Institute of Bioinspired Intelligence and Mining Knowledge) グループによって開発された、MATLABベースの進化的多目的最適化プラットフォームです。200以上の進化アルゴリズムと400以上のベンチマーク問題を提供する、オープンソースの研究・教育用プラットフォームとなっています。

主な特徴

  • 豊富なアルゴリズム：遺伝的アルゴリズム、差分進化、粒子群最適化など
  • 充実したベンチマーク問題
  • 使いやすいGUIインターフェース
  • 並列実験機能
  • Excel/テーブル形式での結果出力

技術要件

  • MATLABのみで動作（追加のライブラリ不要）
  • クロスプラットフォーム対応
  • MATLABが動作する環境であれば利用可能

利用上の注意点

ライセンスと引用

研究目的での利用は無料ですが、論文などでPlatEMOを使用した場合は以下の論文を引用する必要があります：

Ye Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum], IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87

最新バージョン（v4.8）の特徴

  • ブロック接続による新アルゴリズムの視覚的作成
  • 複数ソリューションの同時評価機能
  • 新しい多目的進化アルゴリズム（MOBCA, NRV-MOEA, NSBiDiCoなど）の追加

PlatEMOは継続的に更新されており、最新のアルゴリズムや機能が定期的に追加されています。GitHubのリポジトリをチェックすることで、最新の更新情報を確認できます。

MATLABのFile Exchangeにも上がっているので、アドオンエクスプローラーからも追加できます。
Screenshot 2024_12_12 23_03_51.png

GUIを見てみる

PlatEMOはCUIでも実行できますが、ここではGUIでいろいろ見てみます。
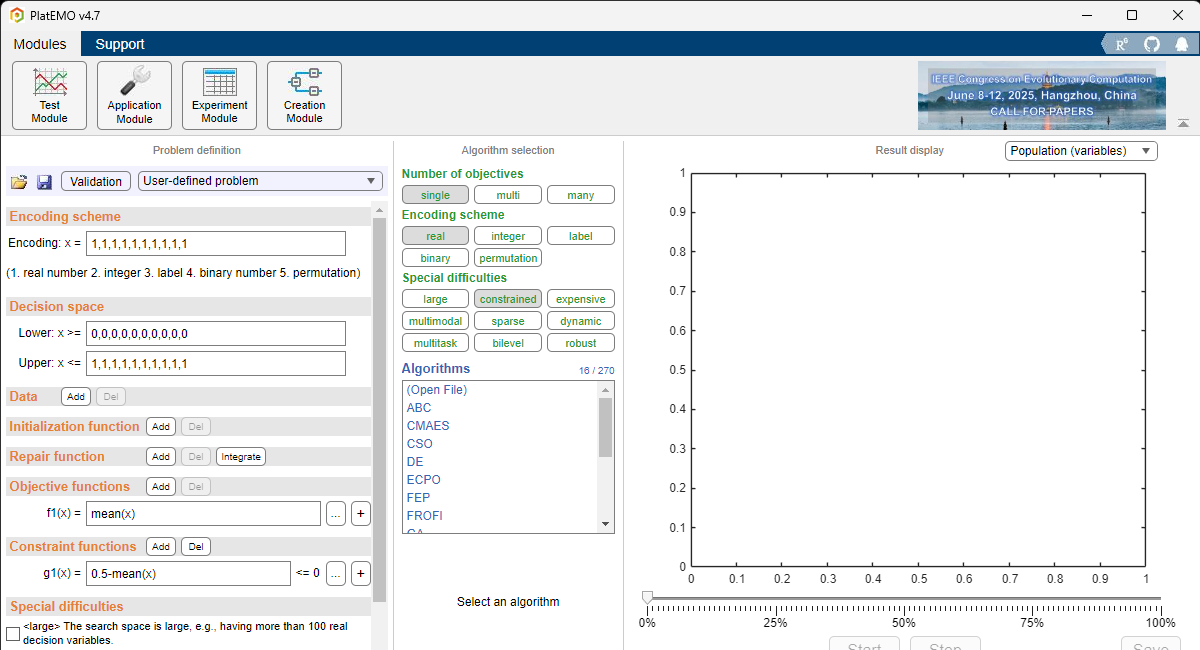
PlatEMO v4.7 2024_12_12 22_40_41.png
この画面では、自身で最適化問題を定義し、実行できます。

ベンチマーク問題を遊んでみる

PlatEMOにはさまざまなベンチマーク問題があります。試しにやってみます。
ベンチマーク問題は、右上のTest Moduleからいろいろ選択できます。
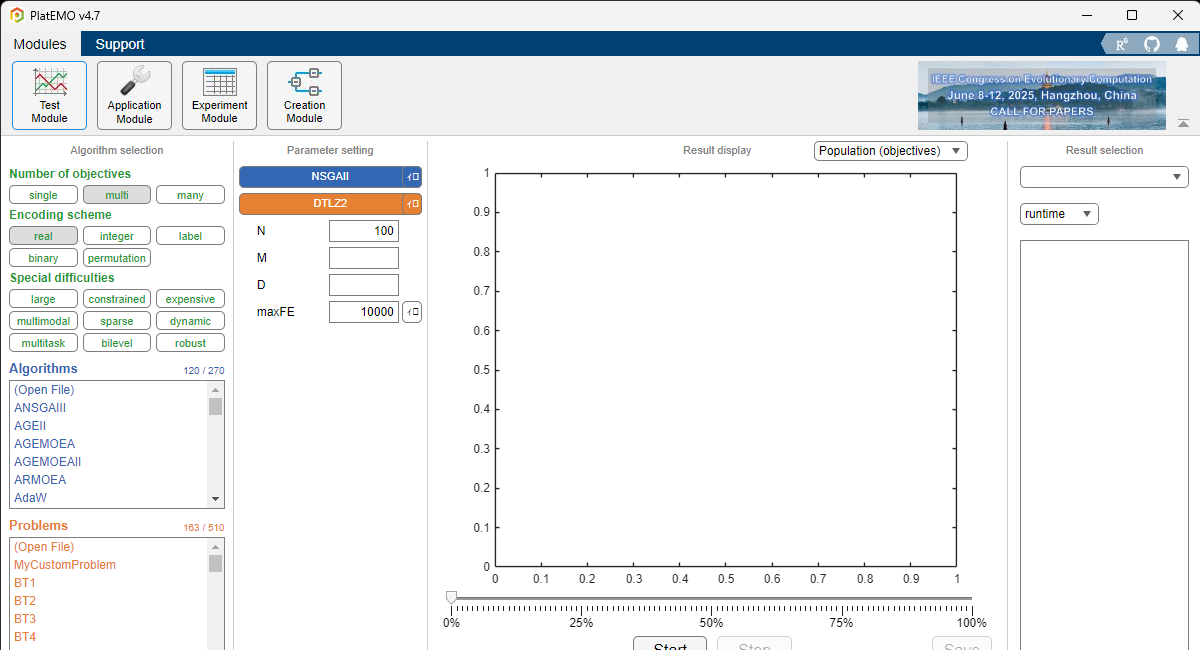
PlatEMO v4.7 2024_12_12 22_40_51.png
左からアルゴリズムとベンチマーク問題を選択し、目的関数と設計変数の数を決めて実行してみます。

2目的の最小化

PlatEMO-v4.7-2024-12-12-22-57-18.gif

3目的の最小化

PlatEMO-v4.7-2024-12-12-23-00-27.gif
たまに突然変異により離れたところにプロットされる個体がいて、そのせいでパレートフロントが伸び縮みしているように見えちゃいますね。

自分で最適化問題を定義して試してみる

エネルギー法による倒立振子の振り上げ

ということで、ここでは

  • 制御則の切り替え角度
  • LQR（最適レギュレータ）による安定化制御の重み
  • エネルギー法による振り上げのゲイン
    これらのパラメータを最適化によって求められないか考えてみます。

こちらの川田先生の記事を参考に台車型（というより、レール型？）の倒立振子の振り上げとそのアニメーションをやってみます。安定化制御と振り上げ制御、無制御の部分の切り替えだったりがうまくいかないと、いい感じに立ってくれません。

設計変数の定義

設計変数として、以下のパラメータを最適化対象とします。

  1. LQRの重み

    • $q_1$: $x$（台車の位置）に対応する重み
    • $q_2$: $\theta$（振り子の角度）に対応する重み
    • $q_3$: $\dot{x}$（台車の速度）に対応する重み
    • $q_4$: $\dot{\theta}$（振り子の角速度）に対応する重み

  2. 振り上げ制御のゲイン

    • $k_e$: エネルギー法で振り上げを行う際のゲイン

  3. 制御則の切り替え角度

    • $\theta_{stable}$: 安定化制御と無制御の切り替え角度
    • $\theta_{swing}$: 無制御と振り上げ制御の切り替え角度

これら7つのパラメータを設計変数として扱い、それぞれの範囲を以下のように定義します：

パラメータ 下限 上限
$q_1$ 1 $10^5$
$q_2$ 1 $10^5$
$q_3$ 1 $10^5$
$q_4$ 1 $10^5$
$k_e$ 0 $10^5$
$\theta_{stable}$ 0 180°
$\theta_{swing}$ 0 180°

目的関数の定義

次に、目的関数を定義します。最適化では、多目的最小化問題として以下を設定します：

  1. 目的関数1: 台車の位置 $x$ の2乗和
    台車の移動距離が小さいほど評価が高くなります。
    $$
    f_1 = \sum_{t}^{t_{end}} x(t)^2
    $$

  2. 目的関数2: 振り子の角度 $\theta$ の2乗和
    振り子が垂直に安定するほど評価が高くなります。
    $$
    f_2 = \sum_{t}^{t_{end}} \theta(t)^2
    $$

コードたち ODE45でシミュレーションを行うために、事前に運動方程式などなどは求めておき、loadで呼び出しています。

ここでは2つの目的関数両方でODE45を実行しているので無駄が多いです。一回で済ませるにはグローバル変数とかキャッシュとか使うんですかね？

costFunction.m
function [cost] = costFunction(variables)
    q1   = variables(1);
    q2   = variables(2);
    q3   = variables(3);
    q4   = variables(4);
    k_e  = variables(5);
    theta_stable = variables(6);
    theta_swing = variables(7);

    load('workspaceData.mat','A','B','StateEqu','params','x0');
    
    % 状態重み行列と入力重み
    Q = diag([q1, q2, q3, q4]);
    R = 1; 

    % LQRゲイン計算
    K = lqr(A, B, Q, R);

    % シミュレーション設定
    tf = 10;
    tspan = 0:0.01:tf;

    % ode45を用いて非線形システムシミュレーション
    [t, x] = ode45(@(t,x) pendulum_cart_nonlinear(t, x, K, StateEqu, params, k_e, theta_stable, theta_swing), tspan, x0);

    % コスト計算 xの2乗和
    cost = sumsqr(x(:,1));

end
costFunction2.m
function [cost] = costFunction2(variables)
    q1   = variables(1);
    q2   = variables(2);
    q3   = variables(3);
    q4   = variables(4);
    k_e  = variables(5);
    theta_stable = variables(6);
    theta_swing = variables(7);

    load('workspaceData.mat','A','B','StateEqu','params','x0');
    
    % 状態重み行列と入力重み
    Q = diag([q1, q2, q3, q4]);
    R = 1; 

    % LQRゲイン計算
    K = lqr(A, B, Q, R);

    % シミュレーション設定
    tf = 10;
    tspan = 0:0.01:tf;

    % ode45を用いて非線形システムシミュレーション
    [t, x] = ode45(@(t,x) pendulum_cart_nonlinear(t, x, K, StateEqu, params, k_e, theta_stable, theta_swing), tspan, x0);

    % コスト計算 thetaの2乗和
    cost = sumsqr(x(:,2));

end

制約条件

制約条件として、入力する力の大きさに上限を設定します。

初期個体

自分でもいろいろとパラメータを調整していたところ、なんとか振り上げできるパラメータを発見したので初期個体の一つにこれを与えてみます。

InvPenAnim.gif

myInitialization.m
function PopDec = myInitialization(N)

    goodSolution = [1,10,1,1000,10,30,135];

    D = 7;
    PopDec = zeros(N,D);

    % 最初の1個体に良好解を割り当て
    PopDec(1,:) = goodSolution;

    % 残りのN-1個はランダムに生成する
    Lower = [1,1,1,1,0,0,0];
    Upper = [1e5,1e5,1e5,1e5,1e5,180,180];
    PopDec(2:end,:) = rand(N-1,D).*(Upper - Lower) + Lower;
end

シミュレーションと最適化の実行

NSGA-IIという多目的最適化用のアルゴリズムを選択し、最適化を実行してみます。

結果

100個体*100世代の10000回の評価で、最終世代ではこのような結果になりました。
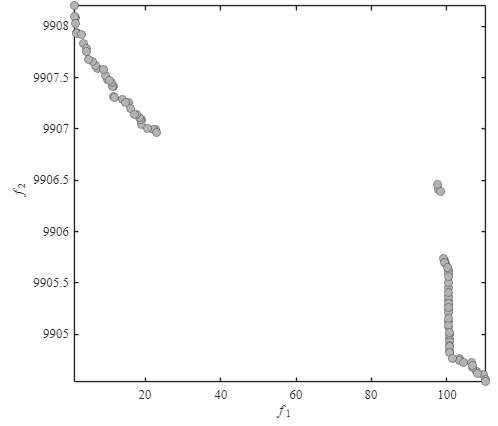
image.png

f2の値は全体でみるとほとんど変わっておらず、f1の値の方が個体ごとに大きく違うように見えます。f1の小さい個体の動画を見てみると、いい感じに最適化されてるなーという感じです。
f2_opti.gif

まとめ

急いで書いたのでコードの詳細など掘り切れていません。。。CUIで使用する場合、使い方がplatemo.mの中にも書いてあるのでそちらを参照してみてください！！！

platemo.m
matlab platemo.m
function varargout = platemo(varargin)
%platemo - The main function of PlatEMO.
%
%   platemo() displays the GUI of PlatEMO.
%
%   platemo('Name',Value,'Name',Value,...) runs an algorithm on a problem
%   with specified parameter settings.
%
% All the acceptable names and values are:
%	'algorithm'     <function handle>	an algorithm
%	'problem'       <function handle>	a problem
%   'N'             <positive integer>  population size
%   'M'             <positive integer>  number of objectives
%   'D'             <positive integer>  number of variables
%	'maxFE'         <positive integer>  maximum number of function evaluations
%   'maxRuntime'    <positive integer>  maximum runtime (in second)
%   'save'       	<integer>           number of saved populations
%   'run'           <integer>           current run number
%   'metName'       <string>            names of metrics to calculate
%   'outputFcn'     <function handle>   function called after each iteration
%   'encoding'      <string>            encoding scheme of each decision variable (1.real 2.integer 3.label 4.binary 5.permutation)
%   'lower'         <vector>            lower bound of each decision variable
%   'upper'         <vector>            upper bound of each decision variable
%   'initFcn'       <function handle>   function for initializing solutions
%   'evalFcn'       <function handle>   function for evaluating solutions
%   'decFcn'        <function handle>   function for repairing invalid solutions
%   'objFcn'        <function handle>   objective functions
%   'conFcn'        <function handle>   constraint functions
%   'objGradFcn'    <function handle>   function for calculating the gradients of objectives
%   'conGradFcn'    <function handle>   function for calculating the gradients of constraints
%
%   Example:
%
%       platemo()
%
%   displays the GUI of PlatEMO.
%
%       platemo('algorithm',@GA,'problem',@SOP_F1,'N',50,'maxFE',20000)
%
%   runs GA with a population size of 50 on SOP_F1 for 20000 evaluations.
%
%       platemo('algorithm',@PSO,'problem',@SOP_F1,'N',100,'maxRuntime',3)
%
%   runs PSO with a population size of 100 on SOP_F1 for 3 seconds.
%
%       platemo('algorithm',{@KnEA,0.4},'problem',{@WFG4,6},'M',5)
%
%   runs KnEA on 5-objective WFG4 and sets the parameters in KnEA and WFG4.
%
%       for i = 1 : 10
%           platemo('algorithm',@MOEAD,'problem',@ZDT1,'save',5,'run',i)
%
5
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?