おさらい
浮動小数点
- コンピュータ世界における少数
- 符号、仮数、指数で表現する 式: $ (-1)^S \times 仮数 \times 2^{指数}$
単精度浮動小数点: 32 bit
倍精度浮動小数点: 64bit
浮動小数点加算
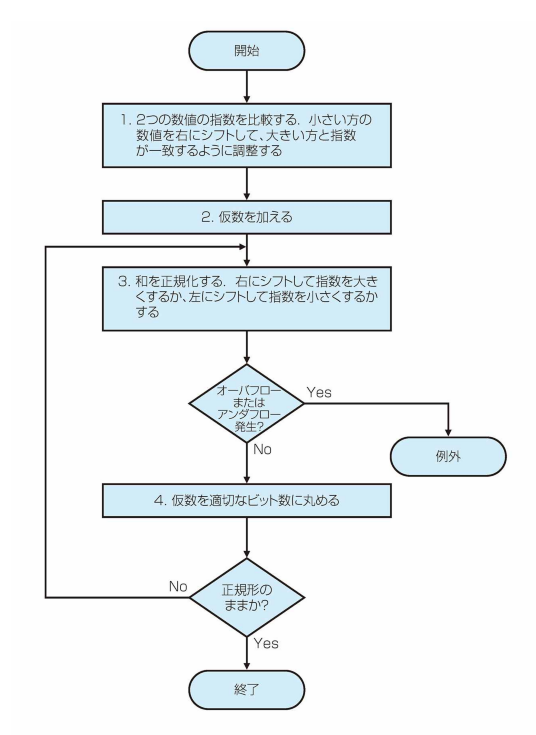
アルゴリズム
例題
- $1.610_{10} \times 10^{-1} + 9.999_{10} \times 10^1 $ の計算
- 仮数には4桁、指数には2桁しか格納できないとする
アルゴリズムに従った計算
1. 指数を比較し、大きい方に合わせる
- $1.610 \times 10^{-1} = 0.1610$ の仮数を右シフトする : $0.016 \times 10^1$
2.仮数を加算
- $9.999 + 0.016 = 10.015$
- 結果: $10.015 \times 10^1$となる
3. 和を正規化する
- $1.0015 \times 10^2$
- アンダフロー or オーバフロー? -> no
- アンダフロ―: 負の指数が大きすぎて指数部に収まらない
- オーバフロー: 正の指数が大きすぎて指数部に収まらない
- 指数が127と-126の間になければならない
4. 仮数を適切なビット数に丸める
- 仮数4桁、指数2桁
- $1.002 \times 10^2$
- 正規化のままか?
- 例: 9.9999を丸めた場合10.000になり正規形ではなくなる
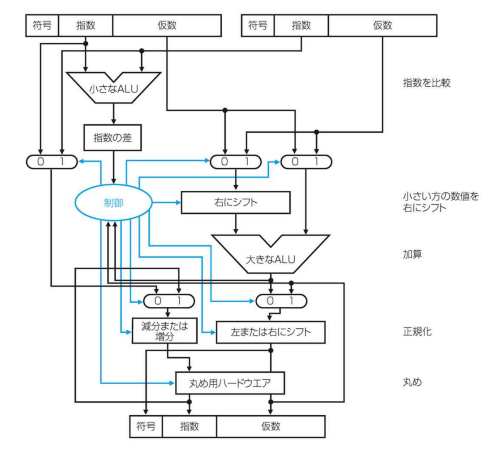
ハードウェア
それぞれのMUXの役割
- 一番左のMUX
- 大きい指数の選択
- 真ん中のMUX
- 小さい方の仮数の選択
- 一番右のMUX
- 大きい方の仮数の選択
- 左下のMUX
- 指数の計算
- 右下のMUX
- 正規化の判定
浮動小数点加算の問題点
- 少数を完璧に表現しきれないことにより計算結果が正確にならない
- 例: $0.01(10)=0.0000001010001111010...(2) $
- 精度と数値範囲のトレードオフ
- 優れた設計には妥協が必要である
浮動小数点乗算
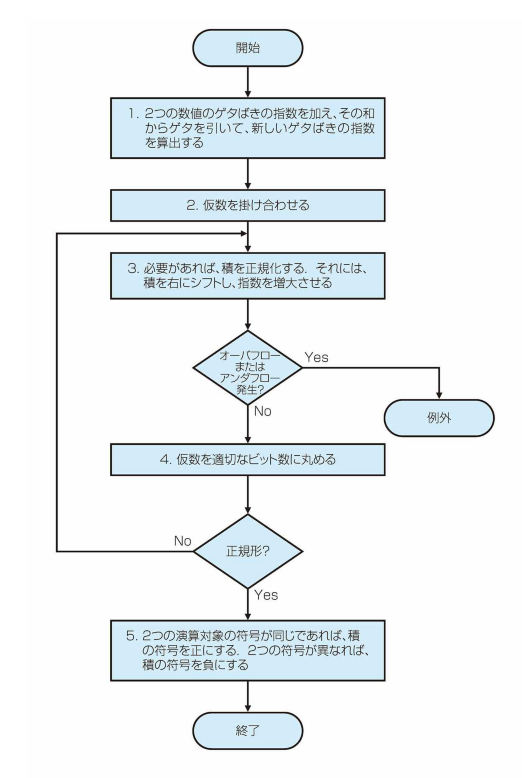
アルゴリズム
例題
- $0.5_{10} \times -0.4375_{10}の計算$
- 2進数で $(1.0000_{2} \times 2^{-1}) \times (-1.110_{2} \times 2^{-2})$
- 仮数には4桁、指数には2桁しか格納できないとする
1. ゲタばき指数の算出
- ゲタばき指数とは
- もっとも小さい負の指数を$00...00$, 最も大きな指数を$11...11$と表す方式
- $(-1)^S \times (1+仮数)\times2^{指数-ゲタ}$
- もっとも小さい負の指数を$00...00$, 最も大きな指数を$11...11$と表す方式
- ゲタなし: -1 + (-2) = -3
- ゲタばき: (-1+127) + (-2+127) -127 = 124
2. 仮数を掛け合わせる
- $ 1.0000 \times 1.110 = 1.110000$
- 仮数は4bitなので1.110となる
3. 正規化
- 必要ない
- オーバフロー or アンダフロー
- 指数 -3は -126以上127以下である
- ゲタばき指数 124は 1以上254である
4. 仮数を適切なビットに丸める
- 丸める必要はない : $ 1.110 \times 2^{-3}$
5. 符号
- $ -1.110 \times 2^{-3} $
MIPSにおける浮動小数点命令
- 四則演算: add.s, add.d, sub.s, sub.d, mul.s, mul.d, div.s, div.d
- 比較: c.neq.s, c.lt.s, c.le.s, c.gt.s, c.ge.s, c.neq.d, ...
- 条件分岐: bclt, bclf
- ロード&セーブ: lwcl, swcl
- レジスタ: $f0, $f1, $f2, ...
- レジスタ2つを組み合わせて倍精度用レジスタを表現する
- $f2と$f3を組み合わせ$f2という名の倍精度レジスタになる
- レジスタ2つを組み合わせて倍精度用レジスタを表現する
例題1: 華氏の気温を摂氏に変換する
f2c:
lwcl $f16, const5($gp) # $f16 = 5.0
lwcl $f18, const9($gp) # $f18 = 9.0
div.s $f16, $f16, $f18 # $f16 = 5.0 / 9.0
lwcl $f18, const32($gp) # $f18 = 32
sub.s $f18, $f12, $f18 # $f18 = fahr - 32.0
mul.s $f0, $f16, $f18 # $f0 = (5/9)*(fahr - 32.0)
jr $ra
例題2: 倍精度汎用行列演算 (DGEMM)
mm:...
# 変数の定義
li $t1, 32 # $t1 = 32
li $s0, 0 # i = 0
L1: li $s1, 0 # j = 0
L2: li $s2, 0 # k = 0
# c[i][j]を$f4にロード
sll $t2, $s0, 5 # $t2 = i * 2^5
addu $t2, $t2, $s1 # $t2 = i * 2^5 + j
sll $t2, $t2, 3 # $t2 = [i][j]のバイトオフセット
addu $t2, $a0, $t2 # $t2 = cのベースアドレス + c[i][j]のアドレス
l.d $f4, 0($t2) # $t2 = 8バイトのc[i][j]
# b[k][j]を$f16にロード
L3: sll $t0, $s2, 5
addu $t0, $t0, $s1
sll $t0, $t0, 3
addu $t0, $a2, $t0
l.d $f16, 0($t0) # $f16 = 8バイトのb[k][j]
# a[i][k]を$f18にロード
sll $t0, $s0, 5
addu $t0, $t0, $s2
sll $t0, $t0, 3
addu $t0, $a1, $t0
l.d $f18, 0($t0) # $18 = 8バイトのa[i][k]
# 行列演算
mul.d $f16, $f18, $f16 # $f16 = a[i][k] * b[k][j]
add.d $f4, $f4, $f16 # $f4 = c[i][j] + a[i][k] * b[k][j]
# k!=32の時L3へ分岐
addiu $s2, $s2, 1
bne $s2, $t1, L3
s.d $f4, 0($t2) # c[i][j] = $f4
# j!=32の時L2へ分岐
addiu $s1, $s1, 1
bne $s1, $t1, L2
# i!=32の時L1へ分岐
addiu $s0, $s0, 1
bne $s0, $t1, L1
補足
- 上記のレイアウトを行優先配置 (row major order) - C言語
- 列ごとにストアされる列優先配置 (column major order) - Fortran
ガード桁を用いた丸め
- 計算の過程で常に2桁分余分にビットを保持
- カード桁
- 丸め桁
- 望ましい近似値を得るための妥協
- 0~1の数字は無限にあるが、浮動小数点形式では2^53個の数字しか表せない
例題
- $0.0256_{10} \times 10^{2} と 2.34_{10} \times 10^2$の加算
- 有効桁数は3桁
ガード桁と丸め桁がない場合
- $ 2.34 \times 10^2 + 0.02 \times 10^2 = 2.36 \times 10^2$
ガード桁と丸め桁がある場合
- $ 2.3400 \times 10^2 + 0.0256 \times 10^2 = 2.3656 \times 10^2$
- ガード桁: 5
- 丸めの桁: 6
- $ 2.37 \times 10^2$
浮動小数点の演算精度
- 仮数の最下位ビット単位 (unit in the last place: ulp) で表される
- IEEE754規格は誤差0.5ulp以内の演算を保証している
補足
- 4つの丸めモード
- 常に切り上げ (+∞方向への丸め)
- 常に切り下げ (-∞方向への丸め)
- 切り捨て (0方向への丸め)
- 最も小さい偶数へ丸め
- 中間の値の(0.5)における丸め
- 常に切り上げしていると公平ではない
- IEEE754では半分を切り上げ、半分を切り下げる措置を取っている
- 左側の数字が奇数の場合は1を加える、偶数の場合は切り捨てる
- スティッキービット
- 0.50..00と0.50..01を区別するためのビット
まとめ
- 浮動小数点の表現は実数の近似値である
- 精度とリソースのトレードオフを考えて、現在IEEE754浮動小数点規格が使われている
3.6 並列処理とコンピュータの算術演算: 半語並列性
時代背景
- 各三原色 -> 8bit, ピクセルの位置 -> 8bit, 音声のサンプルの記録 -> 16bit
- 多くのグラフィックスやオーディオのアプリでは、それらのデータのベクトルに同じ操作を行うことが多いことに気付く
- 128bitの加算器をいくつかのパーティションに区切ることで、短いデータのベクトルを同時に並行して処理できる
- 8bit -> 16個
- 16bit -> 8個
- 32bit -> 4個
- パーティションに区切るコストはわずかである
- 128bitの加算器をいくつかのパーティションに区切ることで、短いデータのベクトルを同時に並行して処理できる
半語並列性 (subword parallelism) / データレベル並列性 / SIMD (6.6章参照)
- SIMD: Single Instruction Multiple Data
- 一つの命令で複数のデータ列に適用するコンピュータの並列化の形態
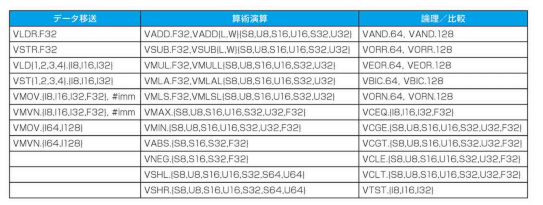
ARM NEON - 半語並列性をサポート
- NEON : ARMのSIMD命令セット
- 256バイトのレジスタを使用
3.7 実例: x86におけるストリーミングSIMD拡張/アドバンストベクトルエクステンション
SSE (Streaming SIMD Extention) 命令
- Intel社のマイクロプロセッサに内蔵された拡張命令セットの一つ
- 主にSIMD処理に関するもの
- 128bitのSIMD処理用レジスタ
- xmm : オペランドの1つが128ビットのSSE2レジスタであることを意味する
- mem/xmm: もう一つのオペランドがメモリ中にあるかまたはSSE2レジスタであることを意味する
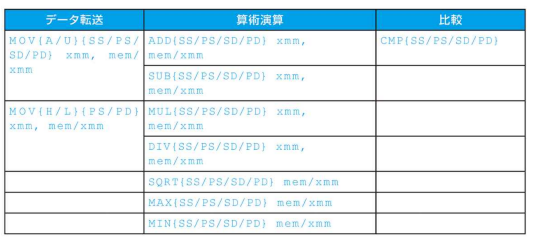
- {} : 基本演算操作の任意変数を示す
- {SS}: スカラの単精度浮動小数点数 - 128bitレジスタ内の1つの32bitオペランド
- {SD}: スカラの倍精度浮動小数点数
- {PS}: レジスタに詰め込まれた単精度浮動小数点数 - 128bitレジスタ内の4つの32bitオペランド
- {PD}: レジスタに詰め込まれた倍精度浮動小数点数
- {A}: 128bitオペランドがメモリ内で整列化していることを意味する
- {U}: 128bitオペランドがメモリ内で整列化していないことを意味する
- {H}: 128bitオペランドの上位半分を移送すること
- {L}: 128bitオペランドの下位半分を移送すること
アドバンストベクトルエクステンション (AVX)
- Intel社の"高い計算能力と低い消費電力を実現する"新しい命令セット
- 256bitのYMMレジスタを導入
- 64bitの浮動小数点加算を2つ実行
- addpd %xmm0, %xmm4
- 64bitの浮動小数点加算を4つ実行
- vaddpd %ymm0, %ymm4
- 64bitの浮動小数点加算を2つ実行
これにより64ビットの浮動小数点加算が4つ生成される
- 3アドレス方式の名声が追加される
- vaapd %ymm0, %ymm1, %ymm4
- (%ymm4 = %ymm0 + &ymm1)
- vaapd %ymm0, %ymm1, %ymm4
- これまでの2アドレス方式
- addpd %xmm0, %xmm4
- (%xmm4 = %xmm4 + %xmm0)
- addpd %xmm0, %xmm4
3.8 高速化: 半語並列性および行列の乗算
- DGEMM (Double Precision GEneral Matrix Multiply) (倍精度汎用行列演算)
Cバージョン
Cバージョンのアセンブリ
vmovsd (%r10), %xmm0 # Cの1要素を%xmm0にロード
mov %rsi, %rcx # B[k+j*n]のアドレスを取る %rcx = %rsi
xor %eax, %eax # %eax = 0
vmovsd (%rcx), %xmm1 # Bの1要素を%xmm1にロード
add %r9, %rcx # B[k+j*n]のアドレス+Bのベースアドレス
vmulsd (%r8, %rax, 8), %xmm1, %xmm1 # %xmm1 = A * B
add $0x1, %rax #
cmp %eax, %edi # 比較 %eax と %edi
vaddsd %xmm1, %xmm0, %xmm0 # xmm1をxmm0に加算
jg 30 <dgemm+0x30> # %eax > %edi ならばジャンプ
add $0x1, %r11 # %r11 = %r11 + 1
vmovsd %xmm0, (%r10) # xmm0をCの要素にストア
最適化されたCバージョン
最適化されたCバージョンのアセンブリ
vmovsd (%r11), %ymm0 # Cの4要素を%ymm0にロード
mov %rbx, %rcx
xor %eax, %eax
vbroadcastsd (%rax, %r8, 1), %ymm1 # Bの要素のコピーを4つ作成
add %0x8, %rax
vmulsd (%rcx), %ymm1, %ymm1 # ymm1 = A * B
add %r9, %rcx
cmp %r10, %rax
vaddpd %ymm1, %ymm0, %ymm0 #
jg 50 <dgemm+0x50> # %r10と%raxが等しくなければジャンプ
add $0x1, %esi
vmovapd %ymm0, (%r11) # ymm0をCの4つの要素にストア
- 最適化されたDGEMMの方が3.85倍速いという結果が出た
3.9 誤信と落とし穴
誤信
- 左シフト命令が2のべき乗を整数に乗ずる働きがあるのと同様に、右シフト命令には2のべき乗で整数を割る働きがある
- -5 ($1011$)を4で割る
- 左に2つシフト: $0010 = 2_{10}$
- 符号ビット拡張して左に2つシフト: $1110 = -2_{10}$
- -5 ($1011$)を4で割る
- 整数データ型に有効な並列処理戦略は、浮動小数点データ型にも有効である
- 結合則が当てはまらない
- 計算の順序によって違う答えがでる
- 浮動小数点形式の演算精度を気にするのは理論数学者だけである
- 浮動小数点除算アルゴリズムが間違っていた
- Intel社は平均的なスプレッドシートユーザーがそのエラーに遭遇するのは27000年に一度だ と否定
- IBMの研究所が24日に1回の頻度でそのエラーに遭遇すると反論
- Intelは非を認めた
- プロセッサーの回収に5億ドルほど要したと言われている
落とし穴
- 浮動小数点の加算には結合則が当てはまらない
- c+(a+b) != (c+a)+b
- $a = 1.5 \times 10^{38}$
- $b = 1.0 $
- $c = -1.5 \times 10^{38} $
- $ c+(a+b) = 0.0 $
- $ (c+a)+b = 1.0 $
- c+(a+b) != (c+a)+b
- MIPSの符号なし即値加算命令(addiu)は16bitを符号拡張する
- MIPSには即値減算目入れがない
- 負の数を加算できるようにするために符号拡張
3.10 おわりに
- 過去十数年にわたって、コンピュータの演算方式は大幅に標準化され、プログラムの移植性が著しく高まった
- 2の補数による2進整数の算術演算
- IEEE754規格に基づく2進浮動小数点算術演算など
- コンピュータによる演算には制度に限界がある
- オーバフロー & アンダフロー
- 並列処理での課題
- 浮動小数点演算の正確性と数値範囲の制約の対処
3.11 歴史展望と三共文献
- インターネット上の3.11節に収録されている