こんにちは、初めまして。
株式会社divの運営する、テクノロジー人材育成スクールTECH::CAMPメンターをしています。
Qiita初投稿ですが、div inc.(TECH::CAMP) Advent Calendar 2018 - Qiitaの記事として投稿させていただきます。
コードが全く登場しないというQiitaの記事っぽくない記事になってしまいました…
はじめに
カナダのD-Waveにより量子コンピューターが実用化[1]され、IBMやGoogleによる研究も進んでおり、量子コンピューターに対する関心が深まっていると思います。ただし、その物理現象について理解されていないところも多い印象があります。
本記事では、量子コンピューターの物理現象、特にキュービットについての概要を量子力学や物理学をあまり勉強していない人にもわかるようになるべく噛み砕いて説明することを目的とします。
自分は今量子コンピューターの基礎の基礎のような研究をしております。そこで学んだことをここでまとめさせていただきます。
対象読者
量子力学や物理学を本格に勉強したことはないが、量子コンピューターの物理に興味がある人。
従来型コンピューターの仕組みを少しでもわかっている人(トランジスタって言葉を知っていれば十分です。)
量子力学そのもの、エネルギーとは何か、原子とはのような話はしません、もし需要があればまとめてみますが…笑
なぜ量子コンピューターが必要なのか
従来型のコンピューターの基本動作原理はトランジスタによるもので、閾値を超えると1、超えないと0のような0,1の2種類で計算を行うシステムです。これは計算だけではなく今自分たちが使っているフラッシュメモリ(USBメモリもこれです)にも応用されています。[2]
(本当は少しだけ構造が違いますが、同じ物理現象を使っています。)
従来のコンピューターで同時に計算できるのは、トランジスタの数だけだと思ってとりあえず大丈夫です。最近のパソコンではトランジスタというよりも、ICチップという名前をきく方が多いと思いますが、ICとはIntegrated Circuit(集積回路)のことで、要するに小さいトランジスタが集積しているものです。そこにどれだけのトランジスタが詰まっているかがコンピューターの基本性能になります。
年々コンピューターの性能が上がっている大きな要因は、このICに集積するトランジスタの数がどんどん多くなっていることにあります。
しかし、同じ大きさのICにより多くのトランジスタを詰め込むということは、一つ一つのトランジスタの大きさがどんどん小さくなることに他ならず、そのサイズは近いうちに原子サイズに到達してしまうのではないかと言われています。[3]
そこで新たな物理が必要となり、その候補の一つに上がっているのが量子コンピューターです。(他にもスピン流というものがあります。この分野もとても面白いので是非調べてみてください。)
量子コンピューターは波動関数(状態)の重ね合わせ(量子計算)を用いて計算を行います。この計算原理についてはわかりやすい説明が多くあるので、ここでは割愛します。これは従来型の計算とは異なり、同時に複数の状態をもつことができるため、一気演算を行うことができる。量子コンピューターは”超並列計算機”とも呼ばれています。
有名な話ですが、並列計算が得意ということは、因数分解や最適化計算が得意なコンピューターです。(興味がある方は、巡回セールスマン問題など調べてみてください。)これはAI(人工知能)やビックデータと非常に相性が良いこともあり、とても期待されているコンピューター技術です。
量子コンピューターの計算を担う量子ビット
さて、ようやく本題です。
そんな量子計算をするための条件は
- 量子情報をロバストに表現できる。
- 普遍的ユニタリー変換の集まりを実行できる。
- 信頼できる初期状態を準備できる。
- 出力結果を測定できる。
など[4]がありますが、簡単にいうと、
量子力学的な性質(量子性)を保ちながら、それを制御(書き込み読み取り)ができる。
ことです。
量子性という言葉を聞きなれない方のために少しだけ説明すると、微小な領域では、物質が「どこ」にいてどんな「運動」をしているのかを一意的に決定することはできない(不確定性原理)ため、その存在は確率で(一定の範囲に確率分布を持って)表されます。
その存在確率が波動関数で記述できることが、今回の量子計算の本質です。
少し難しい話になってきましたが、量子計算とは要するに、onかoffかではなく、「波」の重ね合わせにより計算をするものだと理解していただければ十分かと思います。
現在様々な”仕組み”が検討されていますが、未だ実用化には様々な制約がある状態です。その中でも、IBMやGoogleなどが研究しており、最も有力だと言われているものが「超伝導回路」による量子ビットです。
(ここから超伝導についての説明をすると、さらに長くなってしまうので、ここでは割愛します。)
超伝導回路による量子ビット
超伝導回路による量子ビットにも、「トランズモン量子ビット」「磁束量子ビット」の2種類があります。D-wave社で実現されているものは磁束量子ビットですが、トランズモン量子ビットの方がコヒーレンス時間と呼ばれる量子性を保っていられる時間(=計算可能時間)が長く優位性があるので、今回はこちらを紹介していきます。
量子計算は「1つの原子のもつ2つの状態」を操作することで実現します。この二つの状態のことを”エネルギー準位”と言います。
1つの原子は、一般に複数のエネルギー状態を持ちますが、その中でも特定の2つの状態を取り出して2準位系として使用します。
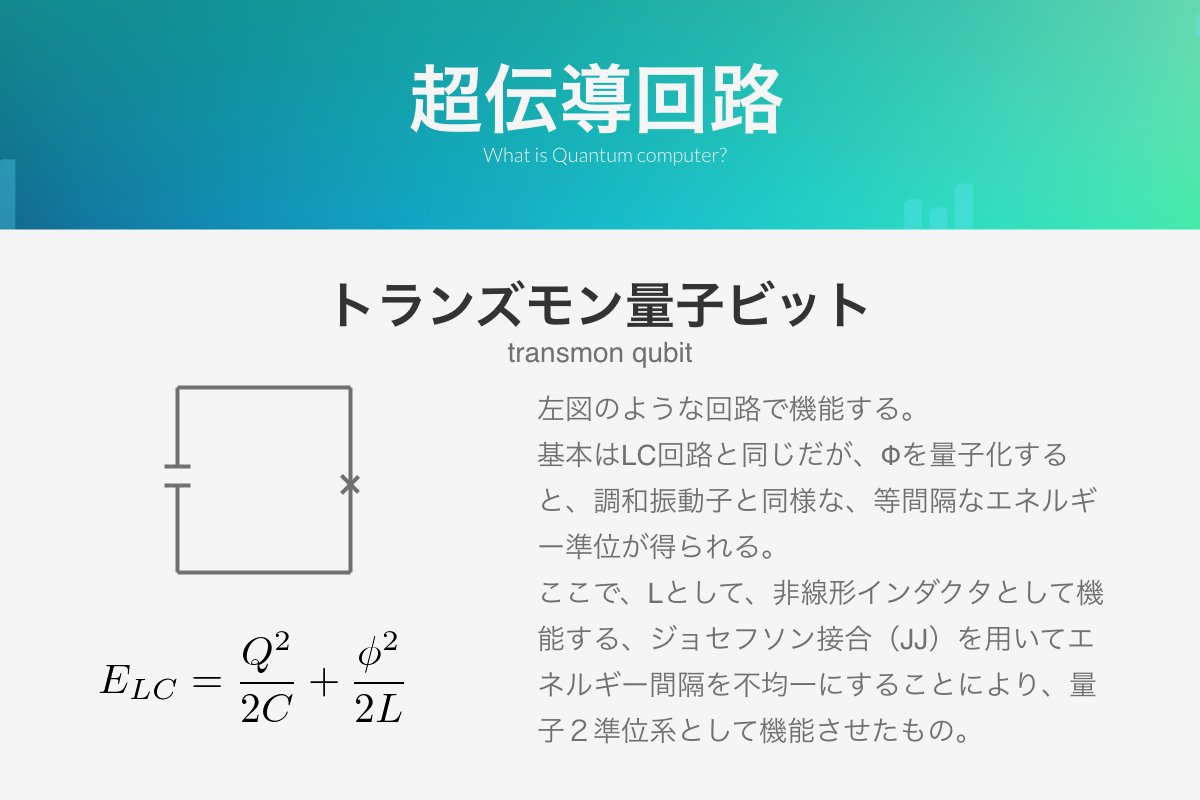
しかし実際の原子の状態を自由に扱うには技術的ハードルが高いため、人工的に2準位系の原子状態を作り出した人工原子を用います。それを実現しているものがトランズモン量子ビットです。少し専門的にいうと、これはLC共振回路のコイルをジョセフソン接合と呼ばれる超伝導体を弱く結合した素子に置き換えることでエネルギー準位を離散化させています。以下に概略図を示します。(表示している式はLC共振回路のエネルギー式です。ばつ印がジョセフソン接合です。)
このようにして超伝導体特有の性質を使ったジョセフソン接合を用いて、離散化準位を実現し、その中で特定の2つの準位を使って量子計算をすることができます。
ではこの人工原子(ここではトランズモン)の量子状態をどう制御するのか。ここもきちんと理解するにはかなり難しい物理を理解する必要があるので、名前とイメージだけお伝えすると、(空洞)共振器量子電磁力学(c-QED: Cavity Quantum ElectroDynamics)と呼ばれるものを応用します。共振器内においた単一原子と、共振器内の光子(≒電場)との相互作用を用いて量子状態を制御します。今ではこれを2次元系に応用して使われる方が集積性に優れるとのことでよく使われています。
このトランズモン量子ビットは発見当初のコヒーレンス時間(=情報の保存時間、計算可能時間)が1nsとかなり短かかったのですが、数々の研究を経て、最近では100μs程度まで改善され、一気に実用化が現実味を帯びています。[5] 確かgoogleやIBMが研究しているのは、もはやこの物理現象ではなく、このトランズモン量子ビットの集積化がメインだったかと思います。今のコンピューターもトランジスタの集積化が成功したことが一気に広がっていった一因だったので、もしこれが実現できれば量子コンピューターの実現にさらに近づきます。
実はこの超伝導量子ビットを最初に発見・提唱したのは日本人です。(当初NEC基礎研究所の中村さん、蔡さん。)
実現に向けての課題
量子コンピューターの実用化が現実みを帯びてきたと言いましたが、まだまだ課題も多いです。よく言われる課題がまず「コヒーレンス時間」です。先ほども触れて少しずつ改善はしてきましたが、これは長ければ長いほど優位なのはいうまでもありません。特に量子コンピューターには「量子誤り」という課題もありこの「誤り訂正」をするための時間も必要です。(従来のコンピューターにも誤り訂正はあります。)
また、超伝導は基本的に極低温で動作します。数mK(ミリケルビン)から高くても数十K(ケルビン)程度です。これは、一般的に使われる表記にすると、ー270度程度の絶対零度付近の領域の話です。もちろん原理的に極低温で動作させないとノイズ(黒体放射によるフォトンなど)が多いのはありますが、冷却コストが大きいことは実用化を阻む要因になります。
このあたりは世界各国で研究が進められているので、今後に期待するしかないですね。自分もほんの少しだけでも貢献できるようがんばります…
終わりに
読んでくださった方、ありがとうございます。
もしここわかりにくいとか、もっと知りたいとかあれば教えてください!笑
致命的な間違いはないつもりですが、本業で研究している人からしたらツッコミどころ満載だと思います、そのあたりは大目に見てください…
研究を本業にしようとは思っていませんが、せっかく勉強したので、これからも少しずつ発信していこうと思います。
少しずつでもわかりやすい読みやすい記事が書けるようになりたい…
*研究の進捗報告で使用したスライドから一部抜粋しております。
参考文献
[1] D-wave Japanホームページ, http://dwavejapan.com/ (unknown)
[2] Forbes 記事 “unsung hero”, Unsung hero (2002年)
[3] nanotec museumサイトより, IC(集積回路)とは? (unknown)
[4] 量子コンピューターと量子通信Ⅱ, Micheal A. Nielsen, オーム社 (2005年)
[5] 大規模量子計算に向けた超伝導量子回路の製作技術,寺井弘高,低温工学53巻5号(2018年)
[6] 量子情報科学の基礎,広田修,森北出版(2002年)