この記事は EEIC Advent Calendar 2023 のシリーズ2の17日目です。
何をしたか
Thrustを使ってビンゴ大会のシミュレーションをしました。
GitHubのレポジトリはこちら
結果だけみたい人は、下の目次から3. , 4. あたりに飛んでください。
目次
きっかけ
最近LLMとかでますます深層学習が話題になっていて、transformersとかPyTorchとかのフレームワークをなんか触ったことあるくらいだと、情報系として物足りなくなってくるかもなと思い始めたので、もう少し低レベルのAPIに触れてGPU使った並列計算への理解度を上げたいと考えていました。
そんな中、寝転びながらYouTube漁っていたら、ヨビノリ先生の動画のサムネ(20個しかないやろと即答したわけですが......)に釣られて動画をみて、動画内で紹介されている通りのシミュレーションを、GPU使って並列計算で出来たら面白そう!と思い一念発起、現在に至ります。
忘年会シーズンですしちょうど良いですね~~~
技術面の理解はまだ浅いので、どちらかと言うと実装してみてどういう結果になったかを主に紹介することになります。
初めはCUDA実装しようと思っていたのですが、調べていくうちにNVIDIAのThrustというライブラリを使えば実装量が減らせるらしいと分かったので、入門として触れてみることにしました。(でも裏で何起こってるかまた見えにくくなる......)
これは、C++のSTLで提供されているデータ構造やアルゴリズムを、インターフェースは普通のSTLを使う時と同じような感じで、GPU上で並列実行して高速化してくれるC++のライブラリです。
CUDA Toolkitをインストールすると自動的に使えるようになります。
ちなみにCUDAプログラミングを調べていて個人的に1番分かりやすかった資料へのリンクを置いておきます:TSUBAME2.0におけるGPUの 活用方法
ビンゴの実装
BINGOカードに書かれている数字の規則を知っていますか?私は知っています。
詳細は省きますが、各列の数字は左の列から順に1~15, 16~30, 31~45, 46~60, 61~75という15種類の数の中から5個ずつ選ばれています。
真ん中はフリー枠となっているのがメジャーなので、全部で約 $5.5 \times10^{26}$ 通りのカードがあることになります。
{}_{15} P_{5} \times {}_{15} P_{5} \times {}_{15} P_{\color{red}{4}} \times {}_{15} P_{5} \times {}_{15} P_{5} \approx 5.5 \times10^{26}
数字の呼び順は $75! \approx 2.5 \times 10^{109}$ 通りなので、合わせて $10^{136}$ 通りくらいあります。
現在の定義では $1 無量大数 = 10^{68}$ ですので、1無量大数無量大数 (typoではない) 通りくらいあることになります。
これを全て試すのは骨が折れるので、乱数を使ったシミュレーションで解析していきます。
ビンゴに出てくる数は基本的にchar型で収まるので、メモリ効率も考えてchar型で実装していきます。
BINGOカードの生成
先ほど紹介したビンゴカードの規則に則り、乱数を使って生成していきます。
乱数を使った実験ではシード値を固定して再現性を確保することが重要です。thrust::default_random_engine rng(seed);という部分ではそれを行なっています。
ビンゴカードは5行5列で計25個のマスがありますが、これを1次元の配列で表します。前から順番に、1行1列、1行2列、...、1行5列、2行1列、2行2列、...、5行4列、5行5列、というように並べていきます。
続いて、各列ごとに15個の数から5個の数を選びます。が、今回は実装を単純化するために、行と列の対称性を用いて転置したビンゴカードを作成していきます。また、こちらも実装の単純化のため、ビンゴカードには0~74の数を記入し、呼び出す数も0~74とします。すなわち、1行目に0~14、2行目に15~29、...というようにしていきます。
これを実装しているのがforループの中です。thrust::sequence(row.begin(), row.end(), row_start * 3);という部分で、$i (i = 0, 1, 2, 3, 4)$ 行目の場合は $i \times 15 \sim i \times 15 + 14$ が順番に並んだ長さ15の配列を作り、それをシャッフルし、thrust::copy(row.begin(), row.begin() + 5, numbers.begin() + row_start);で先頭の5個を選ぶことにより実現しています。
#include <thrust/copy.h> # thrust::copy
#include <thrust/device_vector.h> # thrust::device_vector
#include <thrust/random.h> # thrust::default_random_engine
#include <thrust/sequence.h> # thrust::sequence
#include <thrust/shuffle.h> # thrust::shuffle
thrust::device_vector<char> generateCard(unsigned long seed) {
thrust::default_random_engine rng(seed);
thrust::device_vector<char> numbers(25);
for(char row_start = 0; row_start < 25; row_start += 5) {
thrust::device_vector<char> row(15);
thrust::sequence(row.begin(), row.end(), row_start * 3);
thrust::shuffle(row.begin(), row.end(), rng);
thrust::copy(row.begin(), row.begin() + 5, numbers.begin() + row_start);
}
return numbers;
}
呼ばれる番号の生成
BINGOカードの作成より簡単で、0~74の数をシャッフルするだけです。
#include <thrust/device_vector.h>
#include <thrust/random.h>
#include <thrust/sequence.h>
#include <thrust/shuffle.h>
thrust::device_vector<char> generateNumbers(unsigned long seed) {
thrust::default_random_engine rng(seed); // random number generator
thrust::device_vector<char> numbers(75); // Bingo uses 75 numbers
thrust::sequence(numbers.begin(), numbers.end()); // 0, 1, 2, ..., 74
thrust::shuffle(numbers.begin(), numbers.end(), rng); // shuffle numbers
return numbers;
}
ビンゴの穴あけ & ビンゴ判定
ビンゴの穴あけはビット反転によって実現します。
2の補数表現が使われていますので、$N (-63 \leqq N \leqq 63)$をビット反転させると$ -N-1 $となります。
今回ビンゴで使われる数は0から74ですので、ビット反転させた数は-75から-1までとなります。
これを利用すると、穴が空いているかどうかの判定は0未満であれば穴あき、というように実現できます。
ビット反転は全ビットが1の数(-1)とのXOR演算で計算できます。
各行、各列のビンゴ判定は簡単にfor文を回すだけです。
斜めの列も、左上から右下のものは1行1列(1番目)、2行2列(7番目)、...というような6個ずつのアクセス、右上から左下のものは1行5列(5番目)、2行4列(9番目)、...というような4個ずつのアクセスでfor文で実現可能です。
// check bingo
char all_1 = -1; // 0b11111111
card[12] ^= all_1; // free space
char bingo_at = 75; // result
for(char cnt = 0; cnt < 75; ++cnt) {
// mark number
char num = numbers[cnt], row_start = numbers[cnt] / 15 * 5;
for(int i = row_start; i < row_start + 5; i++) {
if(card[i] == num) {
card[i] ^= all_1; // mark by bit-flip (turns N to -N-1)
break;
}
}
// check row
for(int row_start = 0; row_start < 25; row_start += 5) {
bool bingo = true;
for(int i = 0; i < 5; i++) {
int idx = row_start + i;
bingo &= card[idx] < 0; // marked
}
if(bingo) {
bingo_at = cnt + 1; // cnt starts from 0
return bingo_at;
}
}
// check column
for(int i = 0; i < 5; i++) {
bool bingo = true;
for(int row_start = 0; row_start < 25; row_start += 5) {
int idx = row_start + i;
bingo &= card[idx] < 0; // marked
}
if(bingo) {
bingo_at = cnt + 1; // cnt starts from 0
return bingo_at;
}
}
// check diagonal
bool bingo = true;
for(int i = 0; i < 30; i += 6) {
bingo &= card[i] < 0; // marked
}
if(bingo) {
bingo_at = cnt + 1; // cnt starts from 0
return bingo_at;
}
bingo = true; // need to reset
for(int i = 4; i < 24; i += 4) {
bingo &= card[i] < 0; // marked
}
if(bingo) {
bingo_at = cnt + 1; // cnt starts from 0
return bingo_at;
}
}
あとはthrust::transformを使って大量にシミュレーションを投げていけば、GPUを用いた並列計算が実現できます。
1つのカード、複数の呼び順
人口推計いわく、2023年6月時点での日本の総人口は124511410人らしいので、その分だけシミュレーションしてみます。
こちらのシミュレーションは、1つのビンゴカードに対して、124511410人が好きな順番で75個の数を言っていった場合に、何個目の数でビンゴとなるか統計を取ることに対応します。
別の視点で言うと、自分のカードがどれだけ速くビンゴできるか期待値(確率分布)を求める動作に対応します。
結果はこちら
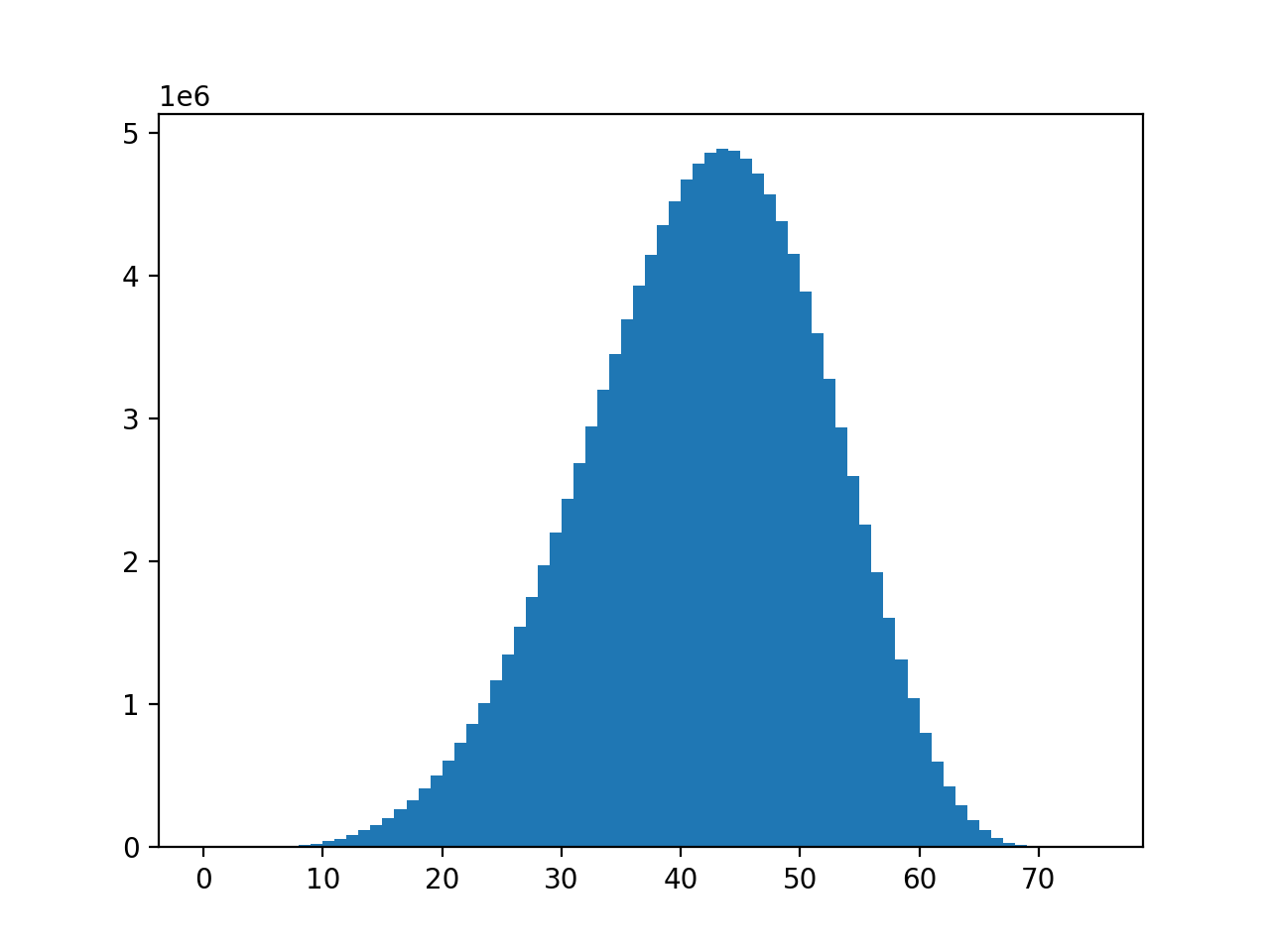
すげ〜!本当に元ネタ動画で解説されてるような感じの山になった!!!
4個目で終わる人、71個目でようやく終わる人、分布の形など、解説通りで気持ち良いですね。
4個目で終わる確率は天和と同じ(約30万分の1)と動画内でも紹介されていましたが、実際に頻度を見てみると400回くらいで、理論通りとなっていました。
最頻値も紹介されていた通りに43となりました。
複数のカード、1つの呼び順
でも実際のビンゴって、みんなバラバラなカードを持って、司会者の番号を真剣に聞きますよね?
ということで、そちらもシミュレーションしてみました。
こちらのシミュレーションは、ある1人が75個の数を順番に読み上げていき、124511410人がそれぞれバラバラな(実際にはランダムなので重複はあるかもですが)のカードの穴を開けていった場合に、何個目の数でビンゴとなるか統計を取ることに対応します。
これが$\dagger$日本人全員でBINGO大会をした$\dagger$ということです。
結果はこちら
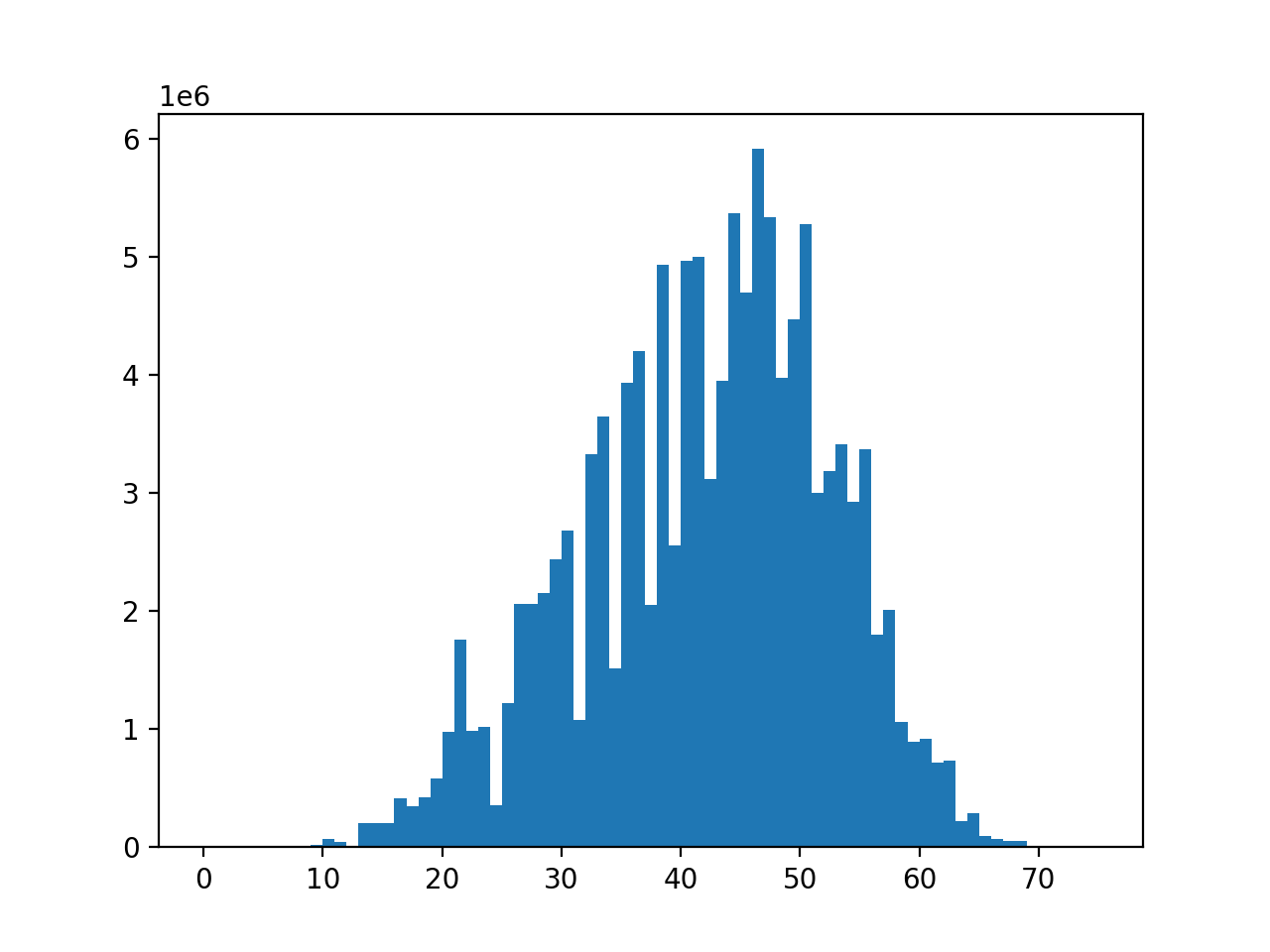
すごい歪な形をしていますね......最初これをみた時は実装バグらせたかなと思ったのですが、よく考えてみると「ランダムに並び替えられた数列の性質」に分布の形が依存することに気づきます。
ちなみに、上図の場合で読み上げられた数列は以下の順番です。
73 19 6 58 22 7 12 39 17 50 29 34 64 53 46
65 24 54 20 26 27 68 61 32 69 4 14 59 51 71
33 9 55 40 63 8 37 21 43 45 67 38 30 47 35
57 42 28 18 25 62 70 44 52 16 66 48 1 13 41
72 15 3 56 11 0 36 49 31 23 74 5 10 2 60
もう少し極端な例を見てみましょう。別のシード値で実験した結果です。
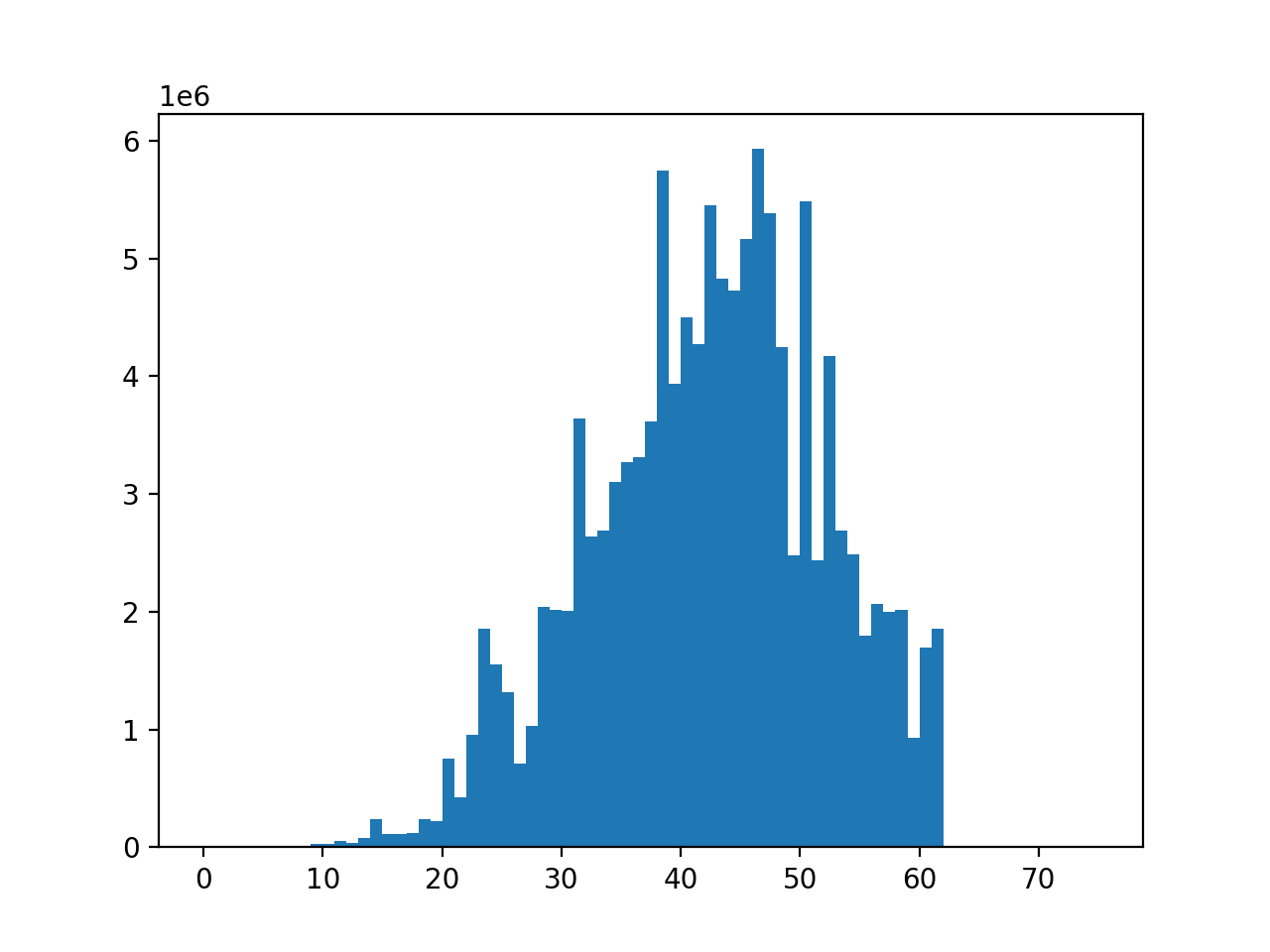
また、読み上げられた数列は以下の順番です。
37 21 27 42 40 24 1 62 54 53 12 23 26 17 14
38 8 47 6 22 34 36 33 15 65 2 50 63 70 73
18 49 55 66 61 43 9 28 68 60 10 71 51 11 5
20 7 59 35 16 31 13 46 56 39 45 48 0 41 3
4 30 74 44 58 69 52 32 64 57 67 19 25 72 29
遅くとも61個目の数字が読み上げられた時点で全員ビンゴを達成しています。
読み上げられた数列に注目してみると、1列目にある0~14の数字が一番最後に読み上げられたのも61番目(4)と一致することに気がつきます。
「数列の性質」というのはこのことを表していて、ある列の数が少し呼ばれやすかったり、呼ばれにくかったりすることで、ビンゴのしやすさが変わってくることが分かります。
たしかに現実のビンゴ大会でも、急にビンゴ達成者が出たかと思えば、あるタイミングだけスン...ってなるタイミングありますよね?
あとここが来ればビンゴなのにな〜って周りを見ると同じ数で待ってる人結構多いみたいな現象も、もしかしたらこれで説明がつくかもしれません。
ビンゴを運営する側になったら、15個ずつに区切られた数の呼び出し数も気にしながらやってみるのも面白いかもしれません。(じゃあ次はIの列〜とか言ってた司会者もいたので、実は気にしている人も既にいそう)
おわりに
結果的にほとんど普通のC++プログラミングする感覚で終わってしまった......
CPUでシミュレーションしたらどのくらいの速さになるのかまでは比較出来なかったのですが、深層学習以外のシミュレーションとかでも、GPUを使った並列計算が(比較的)簡単に実現できることが分かって勉強になりました。
これまではPyTorchとかでなんとなくmodel.to("cuda")とかやっていたのですが、CUDAプログラミングを調べたりThrustを触ったりすることで、裏で何が起こっているのか解像度が上がった気がします。
余裕があればCUDAプログラミングにもちゃんと挑戦してみたいと思います!
あとビンゴのシミュレーションをするだけでも、とても面白い考察がいろいろあって楽しかったです!
追記
初稿でバグ埋め込んでましたすみません。(1行抜けてて右上から左下の斜めビンゴ判定がミスってました。)
乱数シードを選んだ理由です。
- 40: 1個目のシミュレーションが22個目でビンゴするので手作業デバッグ()が簡単だったから。
- 1225: クリスマスだから。
- 2021: EEIC2021の代だから。