Vix先物におけるボリンジャーバンドでの逆張り取引検証

0. 目次

• 1. 概要
• 2. Vixの概念と計算
• 3. ロジック
• 4. データ作成
• 5. シミュレーションコード
• 6. シミュレーション結果
• 7. 追加研究
• 8. 実際に取引してみると
• 9. まとめ

1. 概要

今回はVix先物取引において、ボリンジャーバンドを用いた逆張り取引をPythonを用いてシミュレートする。

結論としては、シミュレーション上では、長い時間足単位で一回の利幅を伸ばすことで、スプレッドや手数料を差し引いても十分な利益が得られることがわかった。ただし、実際に取引をしてみると、エントリーのシグナルが出た際は大抵取引制限がかかっており、注文を執行できなかった。

2. vixの概念と計算

Vixという指標をご存知だろうか。これはS&P500のオプションにおけるインプライドボラティリティ（＝オプション価格を元に算出されるボラティリティ）をもとに算定される指数で、市場のボラティリティを計測している。投資家の間では恐怖指数とも呼ばれている。

詳しい計算は以下。

1. 選択されたオプションの選定：VIXは、S&P 500 インデックス・オプションの中から、満期までの時間が30日以上と30日未満の2つの範囲にあるオプションを選定します。
2. オプションの価格の平均化：選定されたオプションのビッドとアスクの価格の中間値を使用して、オプションの価格の平均を計算します。
3. インプライド・ボラティリティの算出：オプションの平均価格から、ブラック・ショールズ・モデルなどのオプション価格評価モデルを用いてインプライド・ボラティリティを算出します。
4. 重み付けと統合：異なる満期日のオプションに重みを付け、それらを統合して全体のインプライド・ボラティリティを算出します。
5. VIX指数の計算：最後に、得られたインプライド・ボラティリティから、年率換算でVIX指数を計算します。

「富裕層向け資産運用のすべて」より引用

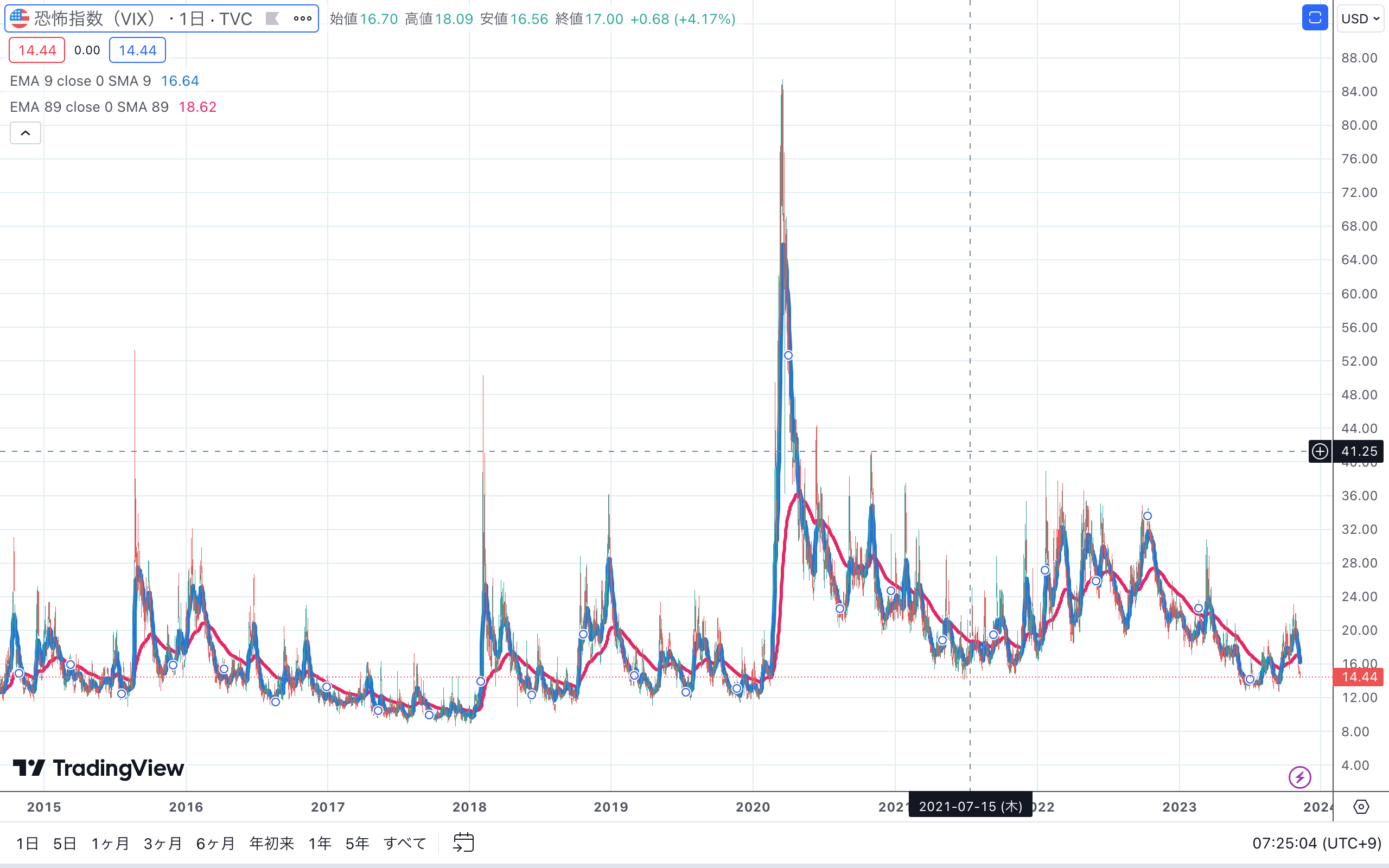
こうして算出されたVixは以下のようなチャートをしている。

Trading View/CBOE-VIXより引用

こうしてみると、プライスの変動幅にある程度上限と下限があるのがわかるだろうか。

今回はこの性質を利用する。プライスが急変動してボリンジャーバンドを突き抜けたら、いずれ戻ることを前提視した逆張りポジションを持つという取引モデルを検証する。

3. ロジック

詳しいロジックは以下。

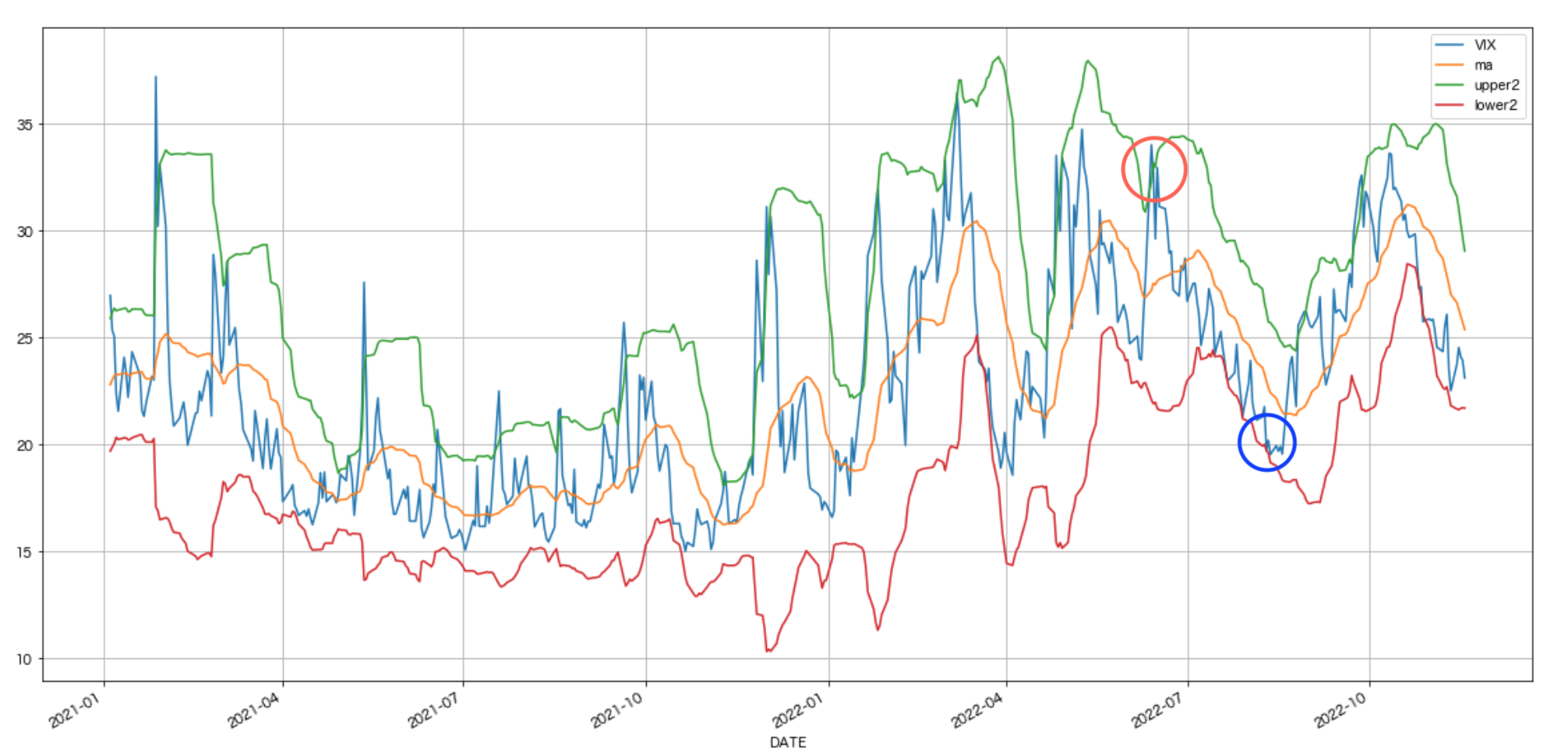
• ボリンジャーバンドを±2σに設定。
• 終値価格がボリンジャーバンドの下限を超えたらLong（下図青◯）
• 終値価格がボリンジャーバンドの上限を超えたらShort（下図赤◯）
• 終値価格が移動平均線に回帰したら決済。
• 途中で含み損が資産総額の40%を超えた場合は損切り。
• ポジションは一度にロングとショートで最大一つずつ、一方向につき既存ポジションを決済するまでは新規ポジションは持たない。
• 手数料、スプレッドは計算外。

グラフ描画(○は手動編集)

data[["VIX", "ma", "upper2", "lower2"]].loc[datetime.datetime(2021,1,1):].plot(figsize=(20,10), legend=True, grid=True)

4. データ作成

• セントルイス連銀より日次レベルのデータを取得。

取得コードは以下。

セントルイス連銀からデータ取得

start = datetime.datetime(1950,1,1)
end = datetime.datetime.now()
data =pdr.DataReader('VIXCLS', 'fred', start, end)
data.columns = ["VIX"]
data

ボリンジャーバンド作成。

ボリンジャーバンド作成

data = data.dropna()
data["ma"] = data["VIX"].rolling(window=20).mean()
data["std"] = data["VIX"].rolling(window=20).std()
data["upper1"] = data["ma"] + data["std"]
data["upper2"] = data["ma"] + data["std"]*2
data["upper3"] = data["ma"] + data["std"]*3
data["lower1"] = data["ma"] - data["std"]
data["lower2"] = data["ma"] - data["std"]*2
data["lower3"] = data["ma"] - data["std"]*3

• GMOクリック証券からも取得。こちらは手動でCSVをサイトからダウンロード。

5. シミュレーションコード

取引シミュレーション

returns = []
unrealizeds = []
long = 0
short = 0
entry_long = 0
entry_short = 0
ret = 0
for i in data.index:
    personal_returns = []
    personal_unrealizeds = []
    #決済
    if short == 1:
        ret_short = (entry_short - data["VIX"][i])/entry_short
        if (data["VIX"][i] < data["ma"][i])|(ret_short < -0.4):
            personal_returns.append(ret_short)
            short = 0
        else:
            personal_unrealizeds.append(ret_short)
            
    if long == 1:
        ret_long = (data["VIX"][i] - entry_long)/entry_long
        if (data["VIX"][i] > data["ma"][i])|(ret_long < -0.4):
            personal_returns.append(ret_long)
            long = 0
        else:
            personal_unrealizeds.append(ret_long)

    if personal_returns != []:
        returns.append(sum(personal_returns))
    else:
        returns.append(0)
    
    if personal_unrealizeds != []:
        unrealizeds.append(sum(personal_unrealizeds))
    else:
        unrealizeds.append(0)
    
    #ロングエントリー
    if short == 0:
        if data["upper2"][i] < data["VIX"][i]:
            short = 1
            entry_short = data["VIX"][i]
    #ショートエントリー
    if long == 0:
        if data["lower2"][i] > data["VIX"][i]:
            long= 1
            entry_long = data["VIX"][i]

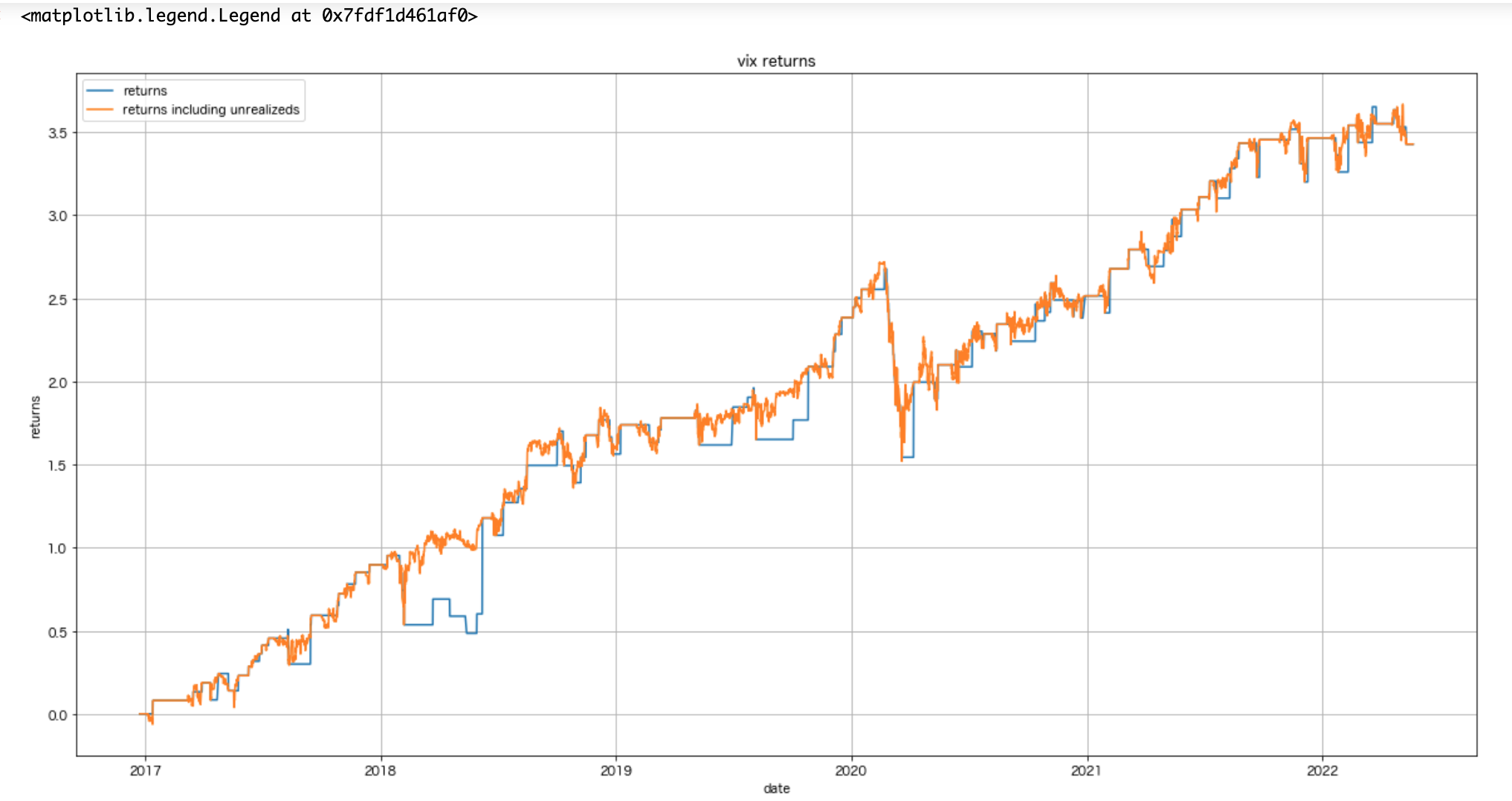
6. シミュレーション結果

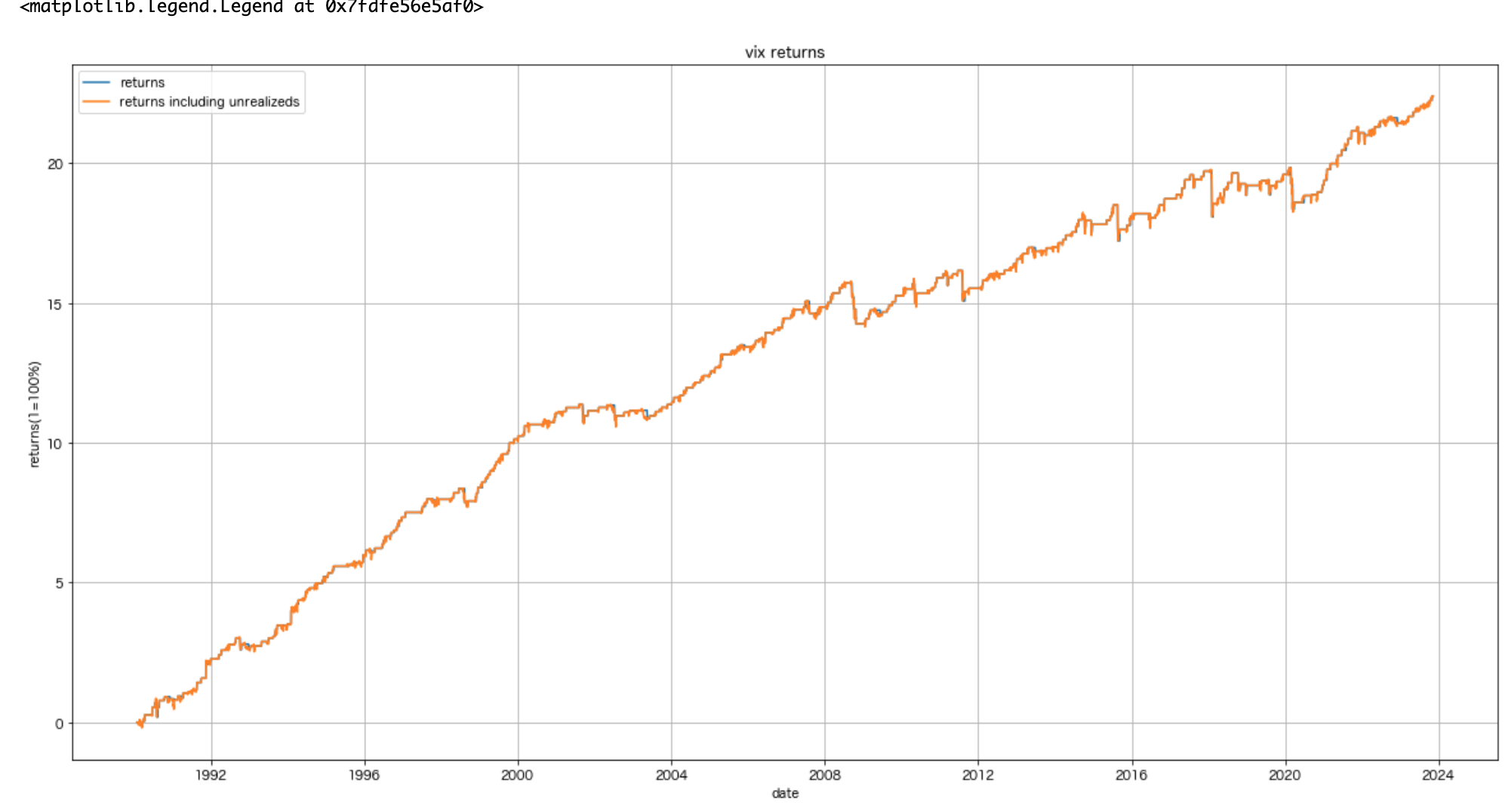
この結果を見ると、長期的に安定したリターンを得られていることがわかる。勝率は約82%。IRは0.058ほど。

利益表(32年間)

利益合計	勝率	Information Ratio
2000%	82%	0.058

結果出力のコードは以下。

結果出力

plt.figure(figsize=(20,10))

plt.plot(data.index, pd.Series(returns).cumsum(), label="returns")
plt.plot(data.index, pd.Series(returns).cumsum() + unrealizeds, label ="returns including unrealizeds")

plt.xlabel("date")
plt.ylabel("returns(1=100%)")
plt.title("vix returns")

plt.grid()

plt.legend(loc=0)

len([i for i in returns if i > 0])/len([i for i in returns if i != 0])

pd.Series(returns).mean()/pd.Series(returns).std()

7. 追加検証

セントルイス連銀の日次データで安定した取引モデルになりうることがわかった。今度はGMOクリック証券の先物データを利用して、スプレッドありで検証してみる。

7-2. データ作成

2017年からのCSVファイルを一つ一つダウンロード。ダウンロードしたファイルを下記の例ようにディレクトリ内に配置

 vix_trade/Vix_data/201606/vix_20160630.csv

直近のデータまでダウンロードできたら、以下のコードでデータを結合。

データ作成

process = False
for i in range(2016,2023):
    for j in range(1,13):
        if j <10:
            mon = "0{}".format(j)
        else:
            mon = "{}".format(j)
        for m in range(1, 31):
            if m < 10:
                day =  "0{}".format(m)
            else:
                day = "{}".format(m)
            try:
                if(i == 2016)&(j==6)&(m==30):
                    df = pd.read_csv("vix_trade/Vix_data/201606/vix_20160630.csv",encoding="shift-jis")
                else:
                    df_updated = pd.read_csv("vix_trade/Vix_data/{0}{1}/vix_{2}{3}{4}.csv".format(i, mon, i, mon, day),encoding="shift-jis")
                process =True
            except:
                process = False
                
            if process:
                if(i == 2016)&(j==6)&(m==30):
                    df = df.set_index("日時", drop=True)
                    df.index = df.index.map(time_change_format)
                else:
                    df_updated = df_updated.set_index("日時", drop=True)
                    df_updated.index = df_updated.index.map(time_change_format)
                    df = pd.concat([df,df_updated], join="outer")
            print("{0}/{1}/{2}".format(i,j,m))

日付をインデックスに指定したり、空欄を含む行を削除したり、インデックスを文字列から日付フォーマットに変更したり、Resampleメソッドで時間単位ごとのデータを作成したりなど細かい処理。

細かい処理

df = df.set_index("日時",drop=True)
df = df.dropna()
def time_change_format(a):
    return datetime.datetime.strptime(a, "%Y-%m-%d %H:%M:00")
df.index = df.index.map(time_change_format)
df_hour = df.copy().resample("H").last().dropna()
df_4hour = df.copy().resample("4H").last().dropna()
df_day = df.copy().resample("D").last().dropna()

ボリンジャーバンドの作成

ボリンジャーバンドの作成

def make_band(df_a, window = 80, sigma=2):
    df = df_a.copy()
    df["bid_ma"] = df["終値(BID)"].rolling(window).mean()
    df["bid_std"] = df["終値(BID)"].rolling(window).std()
    df["bid_upper"] = df["bid_ma"] + df["bid_std"]*sigma
    df["bid_lower"] = df["bid_ma"] - df["bid_std"]*sigma
    df["ask_ma"] = df["終値(ASK)"].rolling(window).mean()
    df["ask_std"] =  df["終値(ASK)"].rolling(window).std()
    df["ask_upper"] = df["ask_ma"] + df["ask_std"]*sigma
    df["ask_lower"] = df["ask_ma"] - df["ask_std"]*sigma
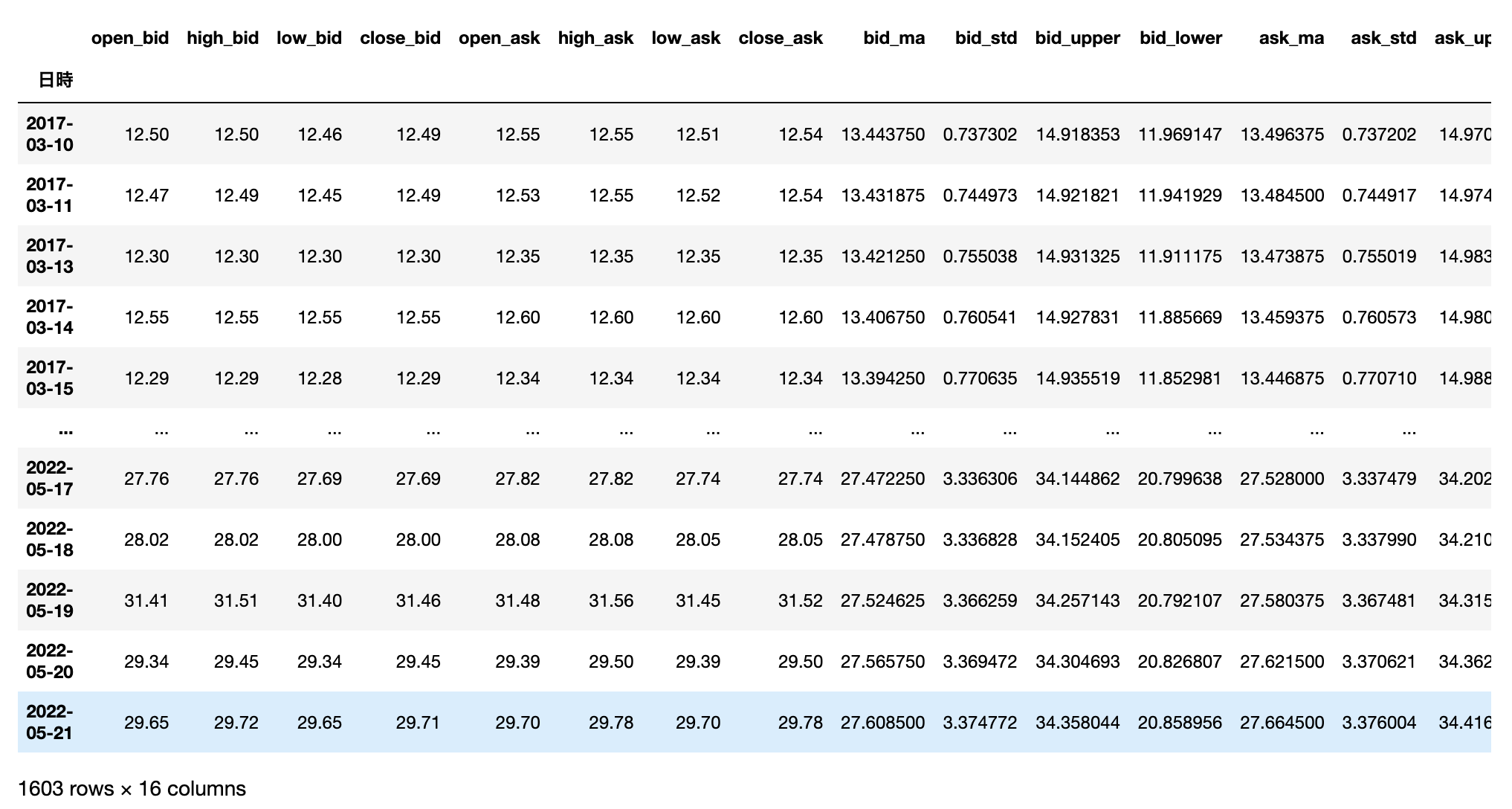
    df.columns = ["open_bid", "high_bid", "low_bid", "close_bid", 
                  "open_ask", "high_ask", "low_ask", "close_ask",
                 "bid_ma", "bid_std", "bid_upper", "bid_lower", "ask_ma","ask_std", "ask_upper", "ask_lower"]
    df = df.dropna()
    return df


df_hour = make_band(df_hour)
df_4hour = make_band(df_4hour)
df_day = make_band(df_day)

作成したデータの中で日足のデータを例にとると以下のようになる。

7-3. ロジックのアップデート

先ほどのシミュレーションではできる限り簡潔になるようシンプルなロジックとしたが、今回はより実践的なシミュレーションを行うために以下を導入。

• 利益確定指値
• 損切り逆指値(10%)
• レバレッジ
• BidとAskはデータに含まれていることから、手数料も自動的に考慮。

7-4. シミュレーションコード

取引シミュレーション

def plot_ret(df_day, rev=2, loss_acceptance=0.1):
    returns = []
    unrealizeds = []
    long = 0
    short = 0
    entry_long = 0
    long_profit = 0
    long_loss = 0
    entry_short = 0
    short_profit = 0
    short_loss = 0
    ret = 0
    for i in df_day.index:
        personal_returns = []
        personal_unrealizeds = []
        #決済
        if short == 1:
            if df_day["low_ask"][i] < short_profit:
                ret_short = (entry_short - short_profit)/entry_short*rev
                personal_returns.append(ret_short)
                short = 0
            elif df_day["high_ask"][i] > short_loss:
                ret_short = (entry_short - short_loss)/entry_short*rev
                personal_returns.append(ret_short)
                short = 0
            else:
                ret_short = (entry_short - df_day["close_ask"][i])/entry_short*rev
                personal_unrealizeds.append(ret_short)
            
        if long == 1:
            if df_day["high_bid"][i] > long_profit:
                ret_long = (long_profit - entry_long)/entry_long*rev
                personal_returns.append(ret_long)
                long = 0
            elif df_day["low_bid"][i] < long_loss:
                ret_long = (long_loss - entry_long)/entry_long*rev
                personal_returns.append(ret_long)
                long = 0
            else:
                ret_long = (df_day["close_bid"][i] - entry_long)/entry_long*rev
                personal_unrealizeds.append(ret_long)

        if personal_returns != []:
            returns.append(sum(personal_returns))
        else:
            returns.append(0)
    
        if personal_unrealizeds != []:
            unrealizeds.append(sum(personal_unrealizeds))
        else:
            unrealizeds.append(0)
    
        #ショートエントリー
        if short == 0:
            if df_day["bid_upper"][i] < df_day["close_bid"][i]:
                short = 1
                entry_short = df_day["close_bid"][i]
                short_profit =  df_day["ask_ma"][i]
                short_loss =  df_day["close_ask"][i]*(1 + loss_acceptance)
            
        #ロングエントリー
        if long == 0:
            if df_day["ask_lower"][i] > df_day["close_ask"][i]:
                long= 1
                entry_long = df_day["close_ask"][i]
                long_profit =  df_day["bid_ma"][i]
                long_loss =  df_day["close_bid"][i]*(1 - loss_acceptance)
    
    return returns, unrealizeds

7-5. シミュレーション結果

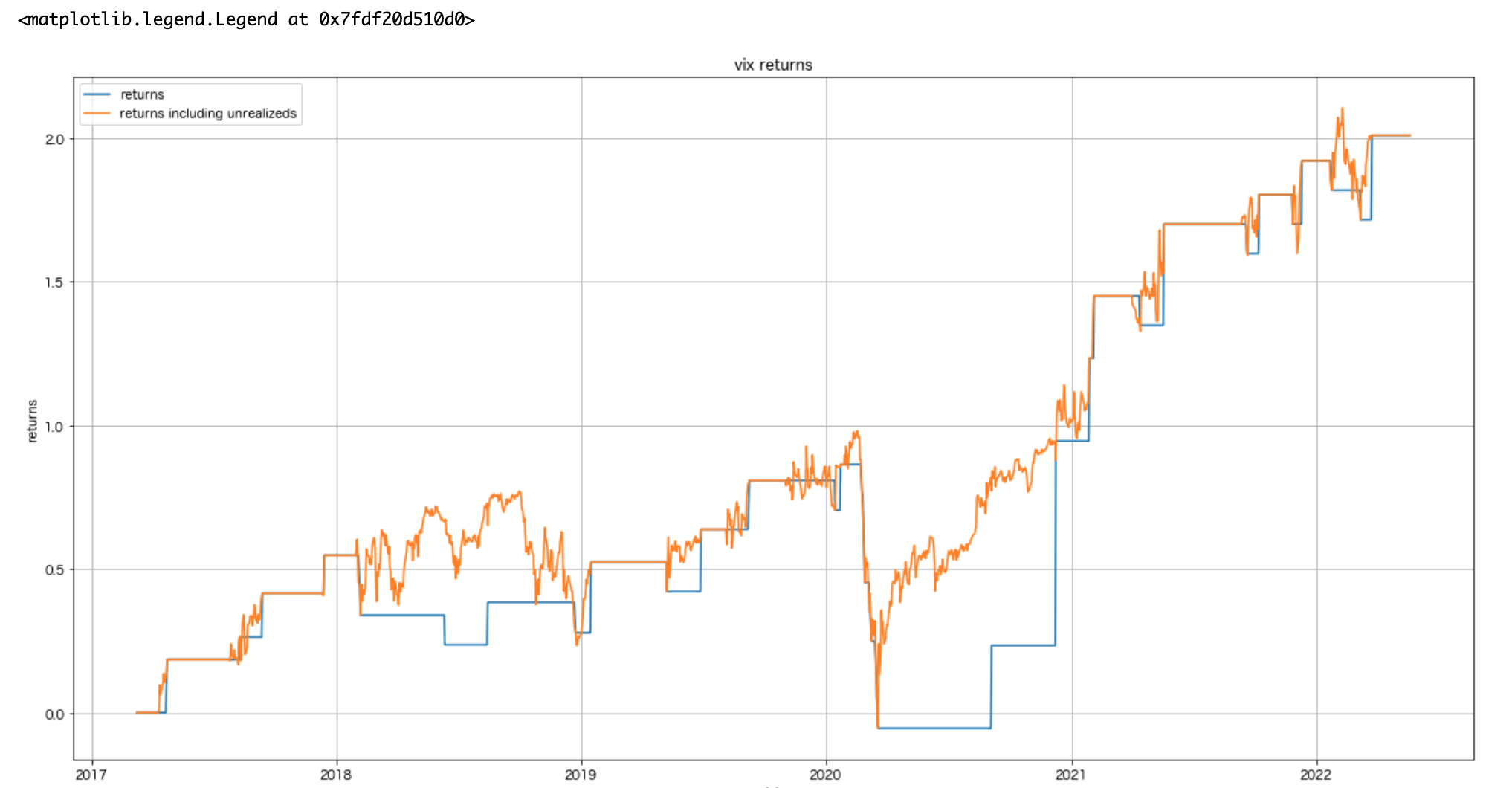
4時間足レベルでの結果

時折ドローダウンを被ってはいるものの、適度に利益は着実に伸びている。細かい指標は以下の通り。グラフにしてみると良好な結果に見えるが、Information Ratioを見てみると0.02とかなり低い。安定したリターンというなら0.1は欲しいところ。

利益表（５年間）

利益合計	勝率	Information Ratio
340%	56%	0.023

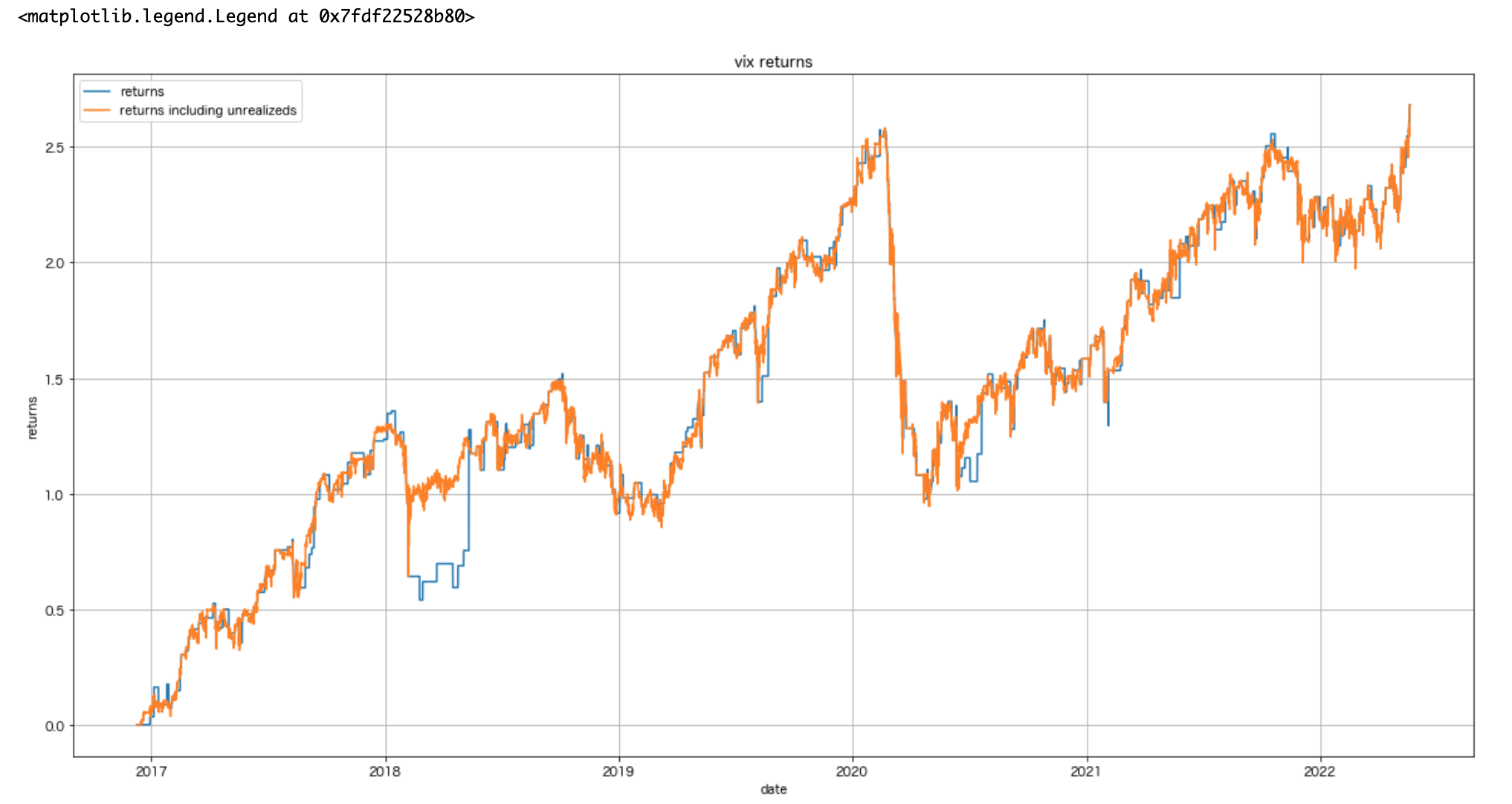
日足レベルでの結果

ドローダウンを常に抱え、時折損失も被ってはいるものの、適度に利益は着実に伸びている。細かい指標は以下の通り。IRが改善したが、グラフを見ればわかる通り、５年間の中で取引回数があまりにも少なく見える。

利益表（５年間）

利益合計	勝率	Information Ratio
200%	45%	0.04

1時間足レベルでの結果

各指標は以下の通り。各指標は以下の通り。取引回数が増えたことで、利益合計は一番高い結果となった。一方で勝率とInformation Ratioは一番低い結果となった。

利益表（５年間）

利益合計	勝率	Information Ratio
268%	66%	0.008

結果の出力コードは以下。

結果の出力

plt.figure(figsize=(20,10))

plt.plot(df_4hour.index, pd.Series(returns).cumsum(), label="returns")
plt.plot(df_4hour.index, pd.Series(returns).cumsum() + unrealizeds, label ="returns including unrealizeds")

plt.xlabel("date")
plt.ylabel("returns")
plt.title("vix returns")

plt.grid()

plt.legend(loc=0)

sum(returns)

len([i for i in returns if i > 0])/len([i for i in returns if i != 0])

np.mean([i for i in returns if i > 0])

np.mean(returns)/np.std(returns)

8. 実際に取引してみると

概ね良好な結果をシミュレーションで得られたため、実際にGMOクリック証券にお金を入金して取引してみた。

結果としては、上手くいかず、シグナルが出た際に注文を執行すること自体ができない場面が多かった。

理由としては、価格がボリンジャーバンドを突き抜ける際は市場が急変動しており、注文が一方向に傾くことが多い。そのため、証券会社の方で取引制限がかかり、一定時間取引ができなくなってしまうのだ。

よって、この取引アルゴリズムはほとんどの場面で使用不可能であるという結論となった。

9. まとめ

Vix先物取引の逆張りは誰もが一度は思いつく取引ある後だとは思うが、こうして定量的に検証してみると、確かに演算上は安定したリターンを積み上げることができるようだ。しかし、いざ取引してみるとシミュレーションのように上手くいかないこともよくわかった。

ただ、取引さえできればリターンが得られることはわかったので、今回利用させていただいたGMOクリック証券以外にVIX先物が取引できるような証券会社があれば、そちらでも検証してみたいと思う。

今回は以上。また次回。

X アカウント

イギリス大学院で学んだ投資の知識や、自己投資などについてX上で毎日呟いているので、フォローよろしくお願いします。

こちらの生活についての報告が少なくてすみません、現在graduate schemeの就活が佳境でして。。

ゆくゆくは生活の足しにもしたいので、自分の海外大学院合格までの軌跡やその後の金銭問題、現在の就活、生活の実態なども100円程のnoteにまとめようと思っています。。

— YuKiYa@🇬🇧で投資を学ぶ大学院生 (@YuKiYa_FX) September 22, 2023