はじめに
プログラミングを使うことの1つのメリットは乱数を用いたシミュレーションや実験が一瞬でできることですね。あることを調べたい時に、試行回数をたくさん積んでシミュレーションを行うことで、理論値がどれほど正しいのかを議論することができます。(コンピューターがない頃は、二項分布の正しさを評価するために何万回もコインを投げて表裏を調べた人もいると言います、、、気の遠くなる作業ですね。)
本記事ではモンテカルロ法を用いて、乱数を用いて円周率を導出しました。
モンテカルロ法・概要
N回シミュレーションを行い、ある事象がM回起これば、その事象の起こる確率はM/Nで近似される性質を持っています。例えばあたりかハズレのみのくじがあるとします。10000回引き、1000回当たりが出れば、このくじの当選率はおそらく1/10程度だと観測値から評価できます。この試行回数が少なければ近似は荒く、試行回数が多ければよい近似となります(中心極限定理)。
観測方法
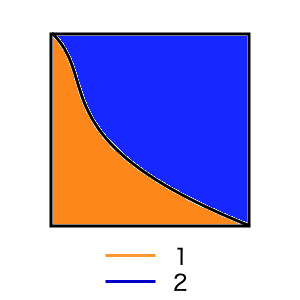
下の画像において、一辺が1の正方形の中に青色とオレンジ色の領域が存在するとします。これらの面積(あるいは面積比)はどのように導出すればよいでしょうか。
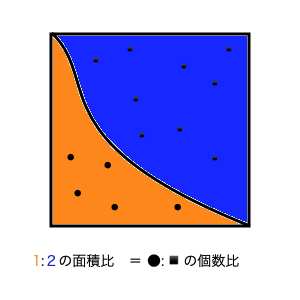
この画像の拡大図を印刷して、小さい正方形のマス目をたくさん書いて個数の比から算出するのがもっとも原始的かつ直接的な方法だと思います。"微小量を足し合わせる"という観点ににおいては今回行うモンテカルロ法と似ている気もします。乱数発生装置を用いて以下のように、平面常にランダムにポイントをプロットしていきます。
そうすると、それぞれの領域にプロットされたポイントの個数の比から、面積比(ひいては面積)を算出することができます。
π値の算出
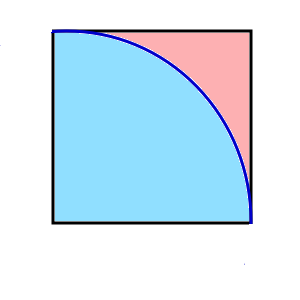
1辺が1cmの四角形の中に円弧を描いた上記のような画像において、水色の領域の面積はいくらになるでしょうか。1 11π/4 = π/4 ですね。つまりプロットした点の個数(N) : 水色の領域に入った点の個数(Ni) = 1 : π/4となります。
πについての式に直すと、 π =4*Ni/N
Pythonコードの実装
import math
import numpy as np
from numpy import random
N_in = 0
N_out = 0
N = 1000 #試行回数
ran_x = random.rand(N) #Xの乱数
ran_y = random.rand(N) #Yの乱数
ran_point = np.hypot(ran_x,ran_y) #X^2 + Y^2の平方根
for i in ran_point:
if i <= 1:
N_in += 1
else:
N_out += 1
Pie = N_in/N*4 #パイの近似式
print("IN: {} ".format(N_in))
print("OUT: {} ".format(N_out))
print("ALL: {} ".format(N))
print("Pi: {} ".format(Pie))
結果:
IN: 797
OUT: 203
ALL: 1000
Pi: 3.188
※試行判定には円の方程式 y^2 + x^2 = 1を用いました。
2つの一様乱数[0~1]の2乗値の合計が1を超えていなければIN、超えていればOUTと見なされます。1000個打ったポイントのうち797個がIN,203個がOUTしたようです。この乱数試行の結果から、πの値が3.188と算出できました。
matplotlibで可視化してみましょう。
import math
import numpy as np
from numpy import random
import matplotlib.pyplot as plt
%matplotlib inline
N_in = 0
N_out = 0
N = 1000 #試行回数
ran_x = random.rand(N) #Xの乱数
ran_y = random.rand(N) #Yの乱数
ran_point = np.hypot(ran_x,ran_y) #X^2 + Y^2の平方根
for i in ran_point:
if i <= 1:
N_in += 1
else:
N_out += 1
Pie = N_in/N*4 #パイの近似式
print("IN: {} ".format(N_in))
print("OUT: {} ".format(N_out))
print("ALL: {} ".format(N))
print("Pi: {} ".format(Pie))
c1 = plt.Circle((0, 0), radius=1, fc="None", ec="r", linewidth=2, color = "black")
ax = plt.gca()
ax.add_patch(c1)
plt.axis("scaled")
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel("X")
plt.ylabel("Y")
plt.title("PLOT")
plt.scatter(ran_x, ran_y, marker=".", color = "green", label = "POINT")
plt.show()
結果:
IN: 775
OUT: 225
ALL: 1000
Pi: 3.10
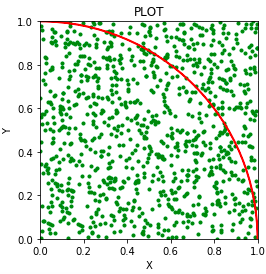
今回は1000個の乱数のうち775個がOUTし、225個がINしました。πの値は3.10となり理論値に近い値が出たと言えます。
πの精度は高いと言えるか?
円周率の値が3.188(1回目),3.10(2回目)なので、理論値の3.141592...から考えると誤差は1%ほどです。ざっくりとした面積を求めたいのであれば良いかもしれませんが、プログラミングコードを組んで算出する値にしてはあまりに荒い値ですね。実際にこの計算を何回も行ってみると・・・
import math
import numpy as np
from numpy import random
import matplotlib.pyplot as plt
%matplotlib inline
from statistics import mean, median,variance,stdev
N_in = 0
N_out = 0
N = 1000 #試行回数
list_pi = []
def culculate():
global N_in, N_out
for i in range(1,100):
ran_x = random.rand(N) #Xの乱数
ran_y = random.rand(N) #Yの乱数
ran_point = np.hypot(ran_x,ran_y) #X^2 + Y^2の平方根
for i in ran_point:
if i <= 1:
N_in += 1
else:
N_out += 1
Pie = N_in/N*4
list_pi.append(Pie)
N_in = 0
N_out = 0
def print_all():
print("IN: {} ".format(N_in))
print("OUT: {} ".format(N_out))
print("ALL: {} ".format(N))
print("Pi: {} ".format(Pie))
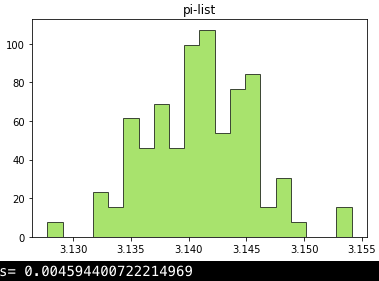
def draw_hist():
kwargs = dict(histtype = "stepfilled", alpha = 0.7, normed = True, bins = 20, color = "red", ec = "black")
plt.hist(list_pi, **kwargs)
plt.title("pi-list")
plt.show()
culculate()
draw_hist()
stdev_pi = stdev(list_pi)
print(stdev_pi)
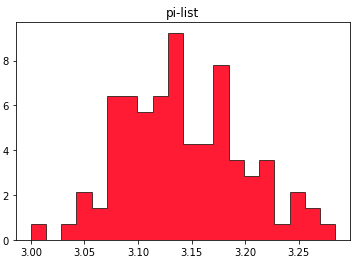
一応理論値の3.14を中心に正規分布っぽくブロードしていますが、調子が悪い時は3.0に近い値をとってしまったり、3.25を超えてしまうようです。
(ちなみに標準偏差を計算したら約0.05でした。これは概算して3回に1回は円周率が[3.09,3.19]の区間を超えてしまうということです。
試行回数を増やした。
プロットする回数が1000回では足りないように思えるので、数を増やしてみました。
N=10000:
IN: 7868
OUT: 2132
ALL: 10000
Pi: 3.1472
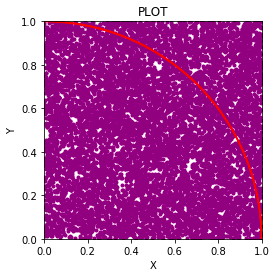
1万回も行えば、モンテカルロ法はほぼ塗り絵みたいな状態になります^^;
N=100000:
IN: 78630
OUT: 21370
ALL: 100000
Pi: 3.1452
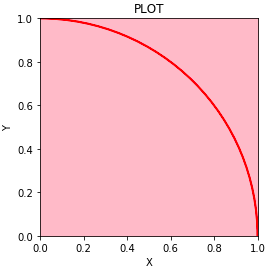
(~_~)。O (信じられるか?これピンクの点を打ってんだぜ・・・)
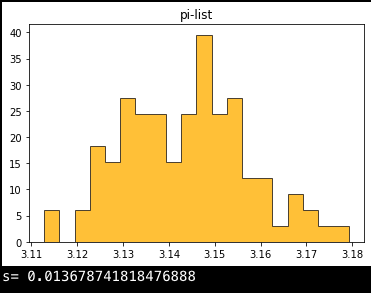
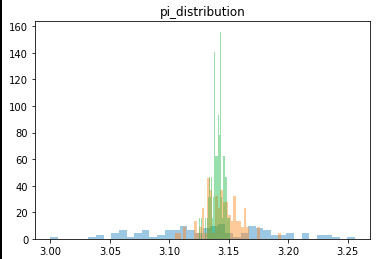
N=1000,10000,100000の時の円周率の値の散らばり具合を確率分布で並べると、かなり精度が良くなっているのがわかります(このグラフ1枚でいいような気もしますが・・・。)
まとめ
今回はモンテカルロ法を用いて円周率を計算しました。その際、円周率の理論値は一切用いていませんが、3.14に収束している様子がわかっていただけたと思います。
10万回やれば、理論値の収束による影響が下2桁台まで出てきましたね。このようにプロットする点の数によって
かなり精度は上がるようです。(ただし標準偏差が下3桁の値になっていることからもわかる通り、小数点の下の値をモンテカルロ法によって正確に出すことは今の僕の実力では難しいようです。
また面白そうなテーマがあれば記事にまとめていこうと思います。