はじめに
こんばんは。最近統計学をやってますが、如何せん理解に時間のかかる分野ですね。。
統計学はデータから導き出す論理なので、最近覚えたPythonと組み合わせて検証なんか面白いのではないかと思って定期的にやることにしました。ブーストラップ法についてです(^0^)
ブートストラップ法について
ブートストラップ法は標本から母集団の性質を推定するための方法です(なので母集団の統計量が未知の時によく使います)。標本集団から標本集団と同じ数だけランダムに値を再抽出し、新しいデータセットを取得し統計値を計算し、これを何回も繰り返し行います。
母集団に属する複雑なパラメータ(相関係数やオッズ比など)に対して標準誤差や信頼区間を求めたりすることが可能で、実用的な方法といえます。今回はデータから算出した相関係数について、どのくらい信頼できるのかを調べました。
相関係数
相関係数はある2つのデータについて、どれだけ関連性が高いかを示す指標です。
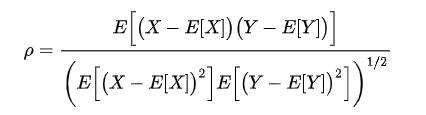
数式だけを見るとなかなか難しそうですが、各値の「平均との差」同士を掛け合わせて合計した共分散を各データの標準偏差で割ればも止まるので、比較的算出は楽です。
ある2変数データがあるとしましょう。例えば10人の生徒が居るとします。英語・数学・理科それぞれのテストを測定した結果、それぞれの点数が出席番号一人目から数えて
英語:[60, 89, 65, 60, 73, 52, 70, 65, 65, 70]
数学:[80, 82, 60, 65, 85, 56, 57, 75, 42, 90]
理科:[90, 87, 60 ,61, 82, 53, 60, 74, 85, 35]
となったとしましょう。
英語と数学、理科について、それぞれがどの程度関係性があるかをそう関係係数を用いてPythonで算出してみましょう。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
scoE = [60, 89, 65, 60, 73, 52, 70, 65, 65, 70] #英語の点数
scoM = [88, 82, 60, 65, 85, 56, 57, 75, 42, 90] #数学の点数
scoS = [90, 87, 60 ,61, 82, 53, 60, 74, 85, 35] #理科の点数
total = np.array([
[60, 89, 65, 60, 73, 52, 70, 65, 65, 70],
[88, 82, 60, 65, 85, 56, 57, 75, 42, 90],
[90, 87, 60, 61, 82, 53, 60, 74, 85, 35]])
np.corrcoef(total)
Numpyのcorrcoef関数を用いると行列式で結果が帰ってきます。
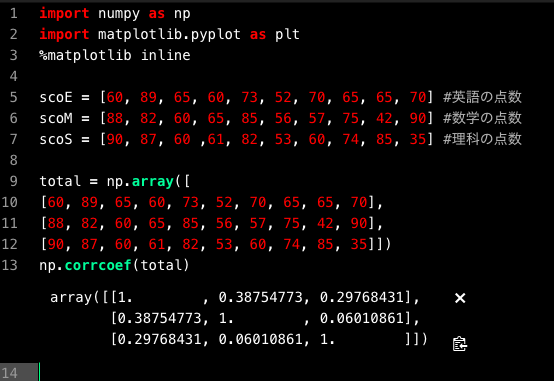
相関係数は
英語-数学:0.3875
英語-理科:0.2977
数学-理科:0.0601
となり、英語と数学の相関が最も高いことがわかりました。(行列の対角成分は1となってますが、自分自身との相関なので自動的に1となります)
本当に相関係数は正しい結論が出ているのか?
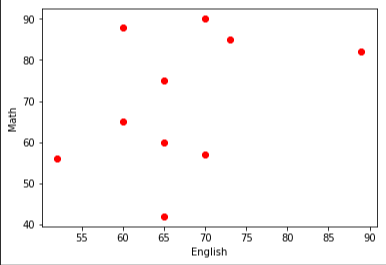
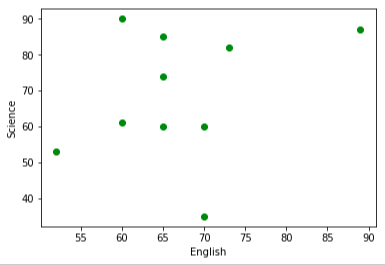
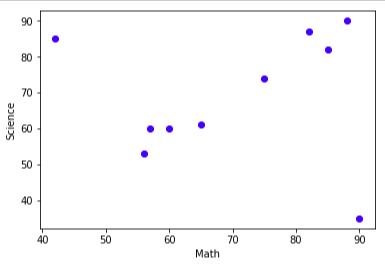
この相関の順番で本当に良いのか?ということすが、このデータに関しては実際にプロットした図をみると違和感を覚えませんかね。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
scoE = [60, 89, 65, 60, 73, 52, 70, 65, 65, 70] #英語の点数
scoM = [88, 82, 60, 65, 85, 56, 57, 75, 42, 90] #数学の点数
scoS = [90, 87, 60 ,61, 82, 53, 60, 74, 85, 35] #理科の点数
total = np.array([
[60, 89, 65, 60, 73, 52, 70, 65, 65, 70],
[88, 82, 60, 65, 85, 56, 57, 75, 42, 90],
[90, 87, 60, 61, 82, 53, 60, 74, 85, 35]])
np.corrcoef(total)
plt.scatter(scoE, scoM,color = "red")
plt.xlabel("English")
plt.ylabel("Math")
plt.show()
plt.scatter(scoE, scoS, color = "green")
plt.xlabel("English")
plt.ylabel("Science")
plt.show()
plt.scatter(scoM, scoS, color = "blue")
plt.xlabel("Math")
plt.ylabel("Science")
plt.show()
となります。実際プロットしてみるとなんか数学と理科が一番関係してそうじゃないですか!?ってことなんですね。。。
違和感を感じた方は、おそらく数学ー理科への直線の当てはまりがとても良さそうなことだと思います。左上、右下の問題児が値を狂わせるだけだと考えます。
ブーストラップ法は特徴量の誤差を評価するためにある。
ブーストラップ法の意味は、非復元無作為抽出を何回も繰り返して標本をたくさん作ることで誤差や信頼区間を求めることができたり、ヒストグラムに直すと信頼度が視覚的にわかるようになります。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from numpy import random
scoE = np.array([60, 89, 65, 60, 73, 52, 70, 65, 65, 70]) #英語の点数
scoM = np.array([88, 82, 60, 65, 85, 56, 57, 75, 42, 90]) #数学の点数
scoS = np.array([90, 87, 60 ,61, 82, 53, 60, 74, 85, 35]) #理科の点数
r_list = []
scoE_data = []
scoM_data = []
for i in range(0,100):
for j in range(0,10): #データから10個のデータをランダムに取り出し標本を作成
var = np.random.randint(0,10)
scoE_data.append(scoE[var])
scoM_data.append(scoM[var])
r = np.corrcoef(scoE_data, scoM_data) #作られた標本を元に相関係数を導出
r_list.append(r[0][1]) #相関係数を"相関係数のリスト"に代入
scoE_data.clear() #初期化
scoM_data.clear() #初期化
print(r_list)
plt.hist(r_list, bins=20, rwidth = 0.9, color = "red", alpha = 0.5)
plt.title("Correlation coefficient(English-Math)")
plt.show()
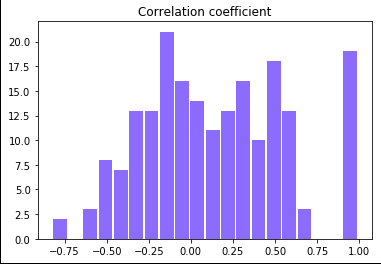
ランダムに作った標本の相関係数が100個されました。
[0.15585253823785258, 0.4305950697037106, -0.03605950604170644, 0.6895914209391649, 0.31730006314271886, 0.3571133940151882, 0.19235034767504772, 0.6604428333327486, 0.34624057748664877, 0.58739740964641, 0.3923342604650358, 0.34982802529568724, 0.37654394258141777, 0.6823344142547625, 0.26931232680365996, 0.3945405713525839, 0.5473013360492976, 0.3972558346301867, -0.014104654480949838, 0.5976257570137701, 0.5372925887633204, 0.28752828548647047, 0.5283345806099249, 0.5940113092694755, 0.7879208402738033, 0.6494747564288043, 0.13714668859593104, -0.07916220211899541, 0.4323235027266908, 0.2981580800528894, -0.036130190979291356, 0.38462886076620495, -0.08602450166292225, 0.1605332861541743, 0.26495611732346275, 0.007258756085075637, 0.4850878590607039, 0.5271967063712417, 0.0560651964634963, 0.5370778152226662, 0.6631130755480596, 0.5518047537543804, -0.4138715864761385, 0.17880183606547947, 0.44587872593154515, 0.8786518859359814, 0.44663361008233027, -0.09199113478155758, 0.44206830104754385, 0.17317850286085323, 0.3527569359486347, 0.02903453532831167, 0.30324100615147653, 0.4659062252828043, 0.36579811733823675, 0.6172409065635549, -0.4304239561846442, 0.4674885654245649, 0.0026228406936778105, -0.16976162750429294, 0.4964958991584344, -0.02845184525323593, 0.2192234013728081, 0.43728466018406714, 0.39454114048797484, 0.5467962835249239, 0.3236567706128534, 0.4905233568089641, 0.25853628119575633, 0.795733061984808, -0.2750759839004001, 0.23758912621891137, 0.5917957647188727, 0.4048812700603928, 0.29588321456141475, 0.5051473660742645, 0.4371408890294217, 0.5345353329276067, 0.31393863261724697, 0.1396781204218693, 0.28503328929367666, 0.16255482611670974, 0.5529714214125769, 0.5610424848640276, 0.2204529677799291, 0.3224797592194247, 0.6352813771554283, 0.3976137186707352, 0.578025141200671, 0.7141681567115036, 0.37172280357440474, 0.15806257086130274, 0.40112964046440924, 0.3112260142848983, 0.5069334332226477, 0.6549800690567563, -0.07955443225108468, -0.12012013025444407, 0.1825061363337386, 0.47319527315037974]
これだけではわけわからないのでヒストグラムで表しました(^▽^)
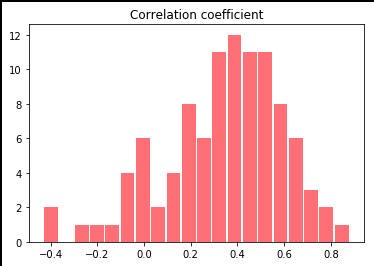
平均が0.4の近くに寄っていますね。先ほど導出した相関係数が0.38だったので
理論値を中心とした正規分布に近い形になっていますね。
次に先ほど違和感のあった数学ー理解の導出です。(サンプルコードはほぼ同じなので省略しました)
こちらは正規分布っぽい形ではありますが、裾が広がっていることがわかりますね。
そして、分散も大きいので、信頼区間も狭いことがわかります。
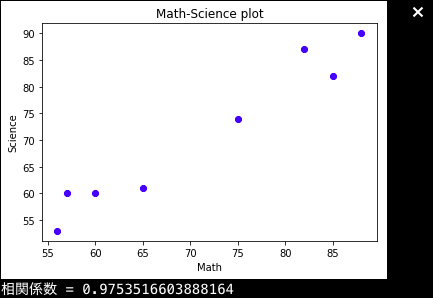
ちなみにですが、先ほどの数学ー理科の問題児を度外視したグラフはこのようになり、
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
scoM = [88, 82, 60, 65, 85, 56, 57, 75] #数学の点数
scoS = [90, 87, 60 ,61, 82, 53, 60, 74] #理科の点数
plt.scatter(scoM, scoS, color = "blue")
plt.xlabel("Math")
plt.ylabel("Science")
plt.title("Math-Science plot")
plt.show()
ブーストラップ法による測定値をヒストグラムに直すと、非常に分散の小さい正規分布になります。
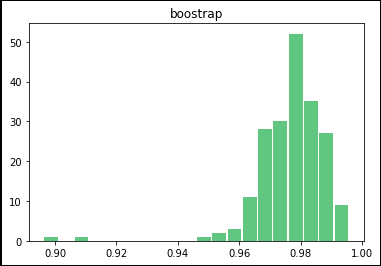
まとめ
ブーストラップ法は、複雑なパラメーターの誤差や信頼区間を求めるためにあるそうです。そして、同じ相関係数を示場合でも、標本の分布によって標準誤差などは違ってくるようです。他にも実用的な測定法があれば載せていく予定なので見ていただければと思いますm(_ _)m