Pythonで「A-Puzzle-A-Day」の日付ごとの難易度を求めてみた

はじめに

「A-Puzzle-A-Day」とは、ノルウェーのある数学者夫婦が作成した、ブロックを適切に当てはめると特定の日付を作成することができる毎日遊べるパズルです。
このパズルをTwitterで見かけてどうしてもやりたくなってしまってたので、100均で木材を購入して自作してみました。

今日の日付や自分の誕生日、家族の誕生日などいろんな日付のパズルを解いていると、日付によって難易度が違いそうだなと思うようになってきました。

そこで、Pythonを利用して366日すべての正解パターン数を求めて、難易度の差を可視化してみました。

ソースは以下のリンクからでも確認できます。

結果

ランキング

【難しいランキング】　　　 【簡単ランキング】

日付	パターン数		日付	パターン数
10/06	7		01/25	216
04/06	8		01/20	195
07/06	12		06/07	192
10/05	13		08/28	189
05/24	14		01/07・01/23	188

最高難度の「10月6日」は、以下のたった7パターンしかありませんでした。

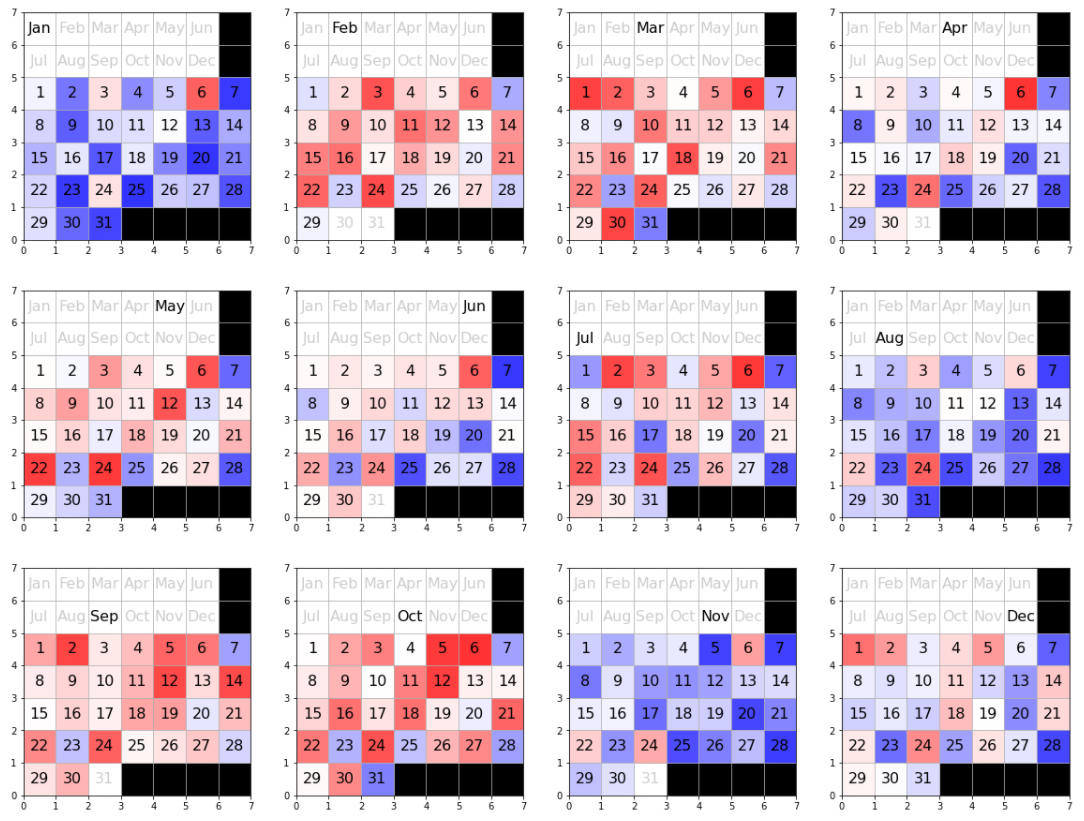
ヒートマップ

易(青)← →難(赤)

全パターン数、日・月ごとの平均

やっぱり月だったり日にちだったりで多少の難易度の偏りがあるようです。
これから9月に入っていきますが、なかなか厳しい戦いが始まりそうですね...。

以降は実装方法の解説です。

実装

0. 事前準備

まずは、ボードの状態とブロックの形を作成します。

initial_board =np.array(
               [[0,0,0,0,0,0,1],
                [0,0,0,0,0,0,1],
                [0,0,0,0,0,0,0],
                [0,0,0,0,0,0,0],
                [0,0,0,0,0,0,0],
                [0,0,0,0,0,0,0],
                [0,0,0,1,1,1,1],
                ])

initial_blocks = [
    np.array([
        [1, 1, 1],
        [1, 1, 1]]),
    np.array([
        [1, 0, 0],
        [1, 0, 0],
        [1, 1, 1]]),
    np.array([
        [1, 1, 0],
        [0, 1, 0],
        [0, 1, 1]]),
    np.array([
        [1, 0, 1],
        [1, 1, 1]]),
    np.array([
        [0, 0, 0, 1],
        [1, 1, 1, 1]]),
    np.array([
        [0, 0, 1, 1],
        [1, 1, 1, 0]]),
    np.array([
        [0, 0, 1, 0],
        [1, 1, 1, 1]]),
    np.array([
        [1, 1, 0],
        [1, 1, 1]]),
]

次に、ブロックは回転させたりひっくり返したりすることでパターンが変わるので、回転させたときの形を取得する関数と、重複なくブロックの回転パターンを洗い出してリストで返す関数を作成します。

# ブロックを回転させる関数
def rotate_block(block, num):
    if num == 0:
        return block
    if num == 1:
        return np.rot90(block,1)
    if num == 2:
        return np.rot90(block,2)
    if num == 3:
        return np.rot90(block,3)
    if num == 4:
        block = np.fliplr(block)
        return block
    if num == 5:
        block = np.fliplr(block)
        return np.rot90(block,1)
    if num == 6:
        block = np.fliplr(block)
        return np.rot90(block,2)
    if num == 7:
        block = np.fliplr(block)
        return np.rot90(block,3)

# 重複なく回転パターンを洗い出す関数
def get_rotate_num(block):
    l = []
    num_l = []
    for i in range(8):
        array1 = rotate_block(block,i)
        flag = True
        for array2 in l:
            if array1.shape == array2.shape and np.allclose(array1,array2):
                flag = False
        
        if flag:
            l.append(array1)
            num_l.append(i)
    return num_l

例えばL字のブロックは、最初の状態から90度、180度、270度回転したパターンの4種類があります。
なので「get_rotate_num」に渡すと4つの番号がリストして返ってきます。
その番号をそれぞれ「rotate_block」に渡すと、回転させたブロックの形が返ってきます。
これらを利用することで、全ブロックを重複なく回転させた全パターンを探索することができます。

block = np.array([
        [1, 0, 0],
        [1, 0, 0],
        [1, 1, 1]])

l = get_rotate_num(block)
print(l)
# [0, 1, 2, 3]

for i in l:
    print(rotate_block(block, i))
"""
[[1 0 0]
 [1 0 0]
 [1 1 1]]

[[0 0 1]
 [0 0 1]
 [1 1 1]]

[[1 1 1]
 [0 0 1]
 [0 0 1]]

[[1 1 1]
 [1 0 0]
 [1 0 0]]
"""

また、事前に求めたい日付の月と日の位置を1に更新しておきます。
そうすることで、すべてのブロックを置き終えてボード上がすべて1となっていることを正解パターンとして探索することができます。

date = datetime.date(2000, 1, 1)

# 月の位置を取得
r = (date.month-1) // 6
c = (date.month-1) % 6
initial_board[r][c] = 1
# 日の位置を取得
r = (date.day-1) // 7 + 2
c = (date.day-1) % 7
initial_board[r][c] = 1

print(initial_board)
'''
[[1 0 0 0 0 0 1]
 [0 0 0 0 0 0 1]
 [1 0 0 0 0 0 0]
 [0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0]
 [0 0 0 1 1 1 1]]
'''

1. まずは全探索

■Time
　1月1日の正解パターンを1つ見つけるのにかかった時間：2時間44分

「get_rotate_num」で各ブロックの回転パターンが取得できるので、それらをitertoolsの「product(直積)」に渡してあげることですべてのパターンを探索をしていきます。

# 各ブロックの回転パターンを保持
l_num = []
for b in initial_blocks:
    l_num.append(get_rotate_num(b))

# 各ブロックの全組み合わせループ
for l in product(l_num[0], l_num[1], l_num[2], l_num[3], l_num[4], l_num[5], l_num[6], l_num[7]):
    # 探索処理

探索の順番としては、左上から右下まで1マスずつずらしながら探索していきます。
指定した位置にブロックを置くと重なる場合、つまりボードの状態で1を超えるマスがあれば、その位置にブロックは置けないと判断して探索しています。

# ボードの状態を見て、継続可能か判定する関数
def judge_correct_board(board, block, position):
    r = position[0]
    c = position[1]
    temp = np.copy(board)
    temp[r:r+block.shape[0],c:c+block.shape[1]] += block

    if np.amax(temp) > 1:
        return False
    return True

block =  np.array([
            [1, 1, 1],
            [1, 1, 1]])
    
print(judge_correct_board(initial_board, block, [0, 0]))
# False
print(judge_correct_board(initial_board, block, [0, 1]))
# True

基本的な全探索でなんとか正解パターンを見つけることができました。
ただ、この判定のみだとかなり非効率な探索となり、1パターン見つけるのに2時間以上かかりました。
探索時間を短縮するために、判定の仕方に工夫を加えていきます。

2. 連結成分のサイズを利用して探索

■Time
　1月1日の正解パターンを1つ見つけるのにかかった時間：21分16秒

パズルのブロックをよく見てみると、2×3のブロック以外は5マス分であることがわかります。つまり、最初に2×3のブロックを置いてしまえば、あとは5マス分のブロックについてだけ考えればいいことになります。
そこで、ブロックを置いた後の残りマスが上下左右にどれだけ繋がっているかを調べて、そのサイズが5の倍数でなければ不正な置き方だと判定する仕組みを追加します。

「残りマスが上下左右にどれだけ繋がっているか」を調べるためには、Union-Findを利用します。
ボード上の0のマスの右側か下側が0だった場合は同じ連結成分として保持し、最後にすべてのマスの連結成分のサイズが5の倍数になっているか判定します。

引用：PythonでのUnion-Find（素集合データ構造）の実装と使い方

# 残るマスの連結成分のサイズが5の倍数かどうか判定する関数
def judge_connected_component(board):
    uf = UnionFind(49)

    for i in range(7):
        for j in range(7):
            if i != 6 and board[i][j]==board[i+1][j]==0:
                uf.union(i*7+j,(i+1)*7+j)
            if j != 6 and board[i][j]==board[i][j+1]==0:
                uf.union(i*7+j,i*7+j+1)

    for i in range(7):
        for j in range(7):
            if board[i][j]==0 and uf.size(i*7+j)%5!=0:
                return False

    return True

この判定を加えることでかなりの時間を短縮することができました。
ただ、まだまだ366日すべての日付を調べ上げるにはあまりにも時間がかかりすぎです。
ここから更なる工夫を加えていきます。

3. 2進数を利用して探索

■Time
　1月1日の正解パターンを1つ見つけるのにかかった時間：0.1秒
　1月1日の全正解パターンを見つけるのにかかった時間：6秒
　366日の全正解パターンを見つけるのにかかった時間：31分46秒

いままでボードの状態を7×7の2次元配列で表現していました。その各マスの0,1を横一直線に並べ49桁の2進数とすることで、ボードの状態を1つの数値としてみなすことができます。

まずは、空の7×7マスにひとつブロックを置いたときの状態を2進数に変換していきます。ひとつのブロックを選んでボードに置くパターンは高々961パターンしかありません。この置き方を全て2進数の数値に変換して、ブロックの種類ごとに保持しておきます。

そして、7つのブロックを置いた時点のボードは、5つの0が残っている2進数となります。
この2進数をビット反転させた数値が先ほど保持した数値の中にあるかどうかを調べるだけで、パズルが完成させられるか判定することができます。

そうすることによって、最後のブロックに関しては左上から1マスずつ当てはめていく探索が必要なくなります。

ブロックが重なってしまうかどうかの判断は、論理積(&)を利用します。
2つの2進数の各桁で両方とも1となる桁がなければ、論理積を取った結果が0となることを利用して判定しています。

num1 = int('110001', 2)
num2 = int('000110', 2)
print(format(num1 & num2, '06b'))
print(num1 & num2)
# 000000
# 0 => OK

num1 = int('110001', 2)
num2 = int('010011', 2)
print(format(num1 & num2, '06b'))
print(num1 & num2)
# 010001
# 17 => NG

ビット反転、つまり各桁の0,1を反転する方法は、排他的論理和(^)を利用します。
すべての桁が1の2進数と排他的論理和(^)を取ることで、0,1を反転することができます。

num1 = int('110001', 2)
num2 = int('111111', 2)
print(format(num1 ^ num2, '06b'))
print(num1 ^ num2)
# 001110
# 14

2進数を利用して探索することで、最後のブロックの探索をかなり省略することができました。
1日の全パターンを見つけるのに10秒かからず、366日すべてのパターンを数え上げるのにも1時間かからず、現実的な時間で探索することができました。

その他TIPS

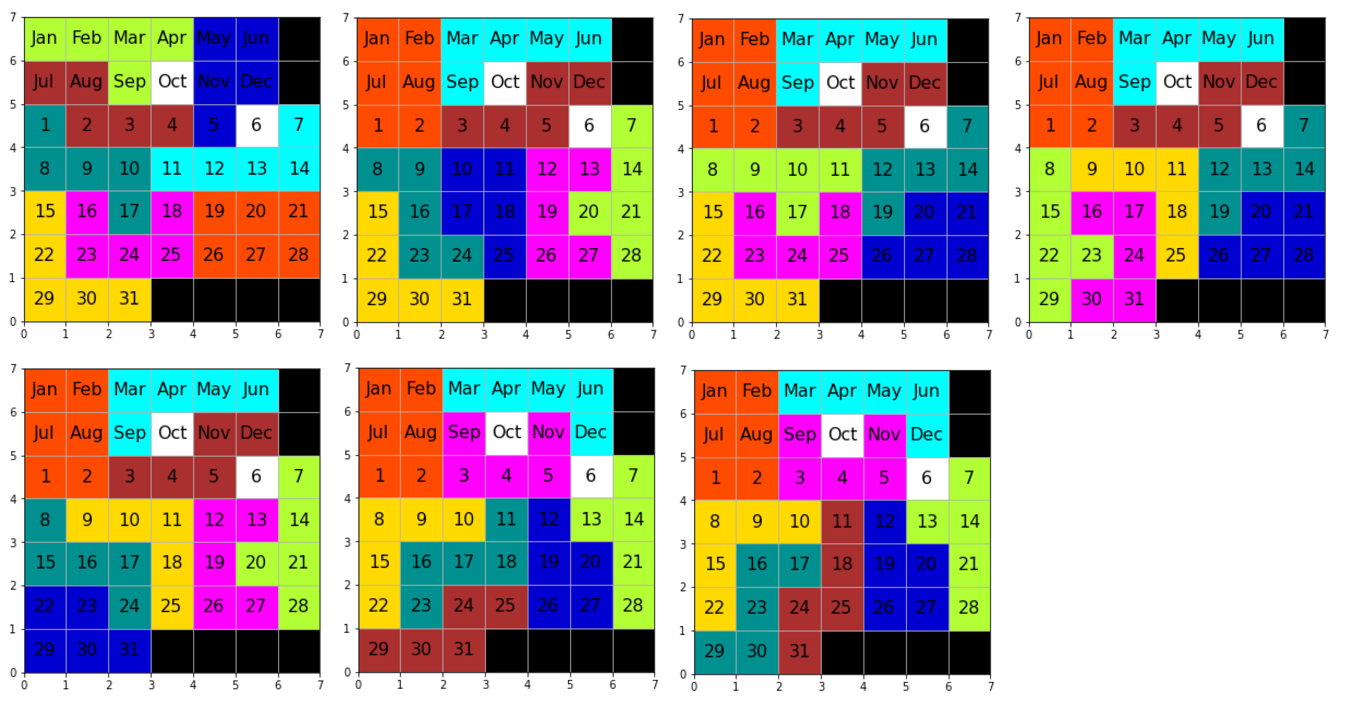
パズルを描画

matplotlibを利用して、パズルの正解例を描画してみました。
日付から座標を計算しつつ、8種類のブロックをそれぞれ異なる色で色分けしてあげるだけ綺麗に描画することができました。

import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta

def draw_puzzle():
    fig = plt.figure(figsize=(5,5))
    ax = fig.add_subplot(111)
    plt.xlim(0,7)
    plt.ylim(0,7)

    ax.set_aspect('equal', adjustable='box')
    ax.grid()

    dt = datetime.date(2000, 1, 1)

    ax.axvspan(6,7,5/7,7/7, color = "black", alpha = 1)
    ax.axvspan(3,7,0/7,1/7, color = "black", alpha = 1)

    # 月の描画
    for i in range(6):
        nm = dt + relativedelta(months=i)
        m = nm.strftime('%b')
        ax.text(0.5+i, 6.5, m, fontsize=16,
                            verticalalignment="center",
                            horizontalalignment="center")
    for i in range(6):
        nm = dt + relativedelta(months=6+i)
        m = nm.strftime('%b')
        ax.text(0.5+i, 5.5, m, fontsize=16,
                            verticalalignment="center",
                            horizontalalignment="center")
        
    # 日の描画
    for i in range(31):
        x = 0.5 + i%7
        y = 0.5 + abs(4-i//7)
        ax.text(x, y, str(i+1), fontsize=16,
                            verticalalignment="center",
                            horizontalalignment="center")
    
    return ax

def draw_blocks(ax, block_nums):
    # 初期化
    ax.axvspan(0,7,0,5, color = 'white', alpha = 1)
    ax.axvspan(6,7,5/7,7/7, color = "black", alpha = 1)
    ax.axvspan(3,7,0/7,1/7, color = "black", alpha = 1)

    colors = ['orangered', 'gold', 'darkcyan', 'magenta', 'aqua', 'brown', 'greenyellow', 'mediumblue',]
    for i in range(len(block_nums)):
        binary = format(block_nums[i], '049b')
        indexs = [i for i, x in enumerate(binary) if x == '1']
        for index in indexs:
            x = index%7
            y = 6 - index//7
            ax.axvspan(x,x+1,y/7,(y+1)/7, color = colors[i], alpha = 1)

    plt.pause(0.1)

ax = draw_puzzle()
block_nums = [62053687492608, 70926016184320, 566362112, 169607168, 270549376, 101888, 144044680282112, 12400]
draw_blocks(ax, block_nums)

この描画を探索の途中に挟めば、どういった順番で探索しているのか視覚的に捉えることができます。

ヒートマップを作成

1年366日をパターン数に応じて順位付けします。
あとでカラーマップに対応させるため、順位を0～255の値に変換しておきます。

# パターン数で順位付け、最大が255になるように調整
df['rank'] = df['pattern_num'].rank(method='min',ascending=False)
_max = df['rank'].max()
df['rank'] = df['rank'] * 255 / _max
df['rank'] = df['rank'].map(int)

カラーマップは以下のサイトを参考にして作成しました。
Colormap カラーマップ

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import datetime
import calendar
from dateutil.relativedelta import relativedelta

# カラーマップを作成
def gen_cmap_rgb(cols):
    nmax = float(len(cols)-1)
    cdict = {'red':[], 'green':[], 'blue':[]}
    for n, c in enumerate(cols):
        loc = n/nmax
        cdict['red'  ].append((loc, c[0], c[0]))
        cdict['green'].append((loc, c[1], c[1]))
        cdict['blue' ].append((loc, c[2], c[2]))
    return mpl.colors.LinearSegmentedColormap('cmap', cdict)

cmap = gen_cmap_rgb([(0.2,0.2,1),(0.8,0.8,1),(1,1,1),(1,0.8,0.8),(1,0.2,0.2)])

gradient = np.linspace(0, 1, 256)
gradient = np.vstack((gradient, gradient))

fig, ax = plt.subplots()
ax.imshow(gradient, aspect=10, cmap=cmap)
ax.set_axis_off()

あとは、順位を変換した値に対応するカラーマップの色を付けていくことでヒートマップを作成することができます。
対象でない月や存在しない日の文字色を薄くすることで見やすくしています。

# ヒートマップを作成
def draw(fig, dt, l):
    ax = fig.add_subplot(3,4,dt.month)
    plt.xlim(0,7)
    plt.ylim(0,7)
    plt.subplots_adjust(wspace=0.2, hspace=-0.4)

    ax.set_aspect('equal', adjustable='box')
    ax.grid()

    ax.axvspan(6,7,5/7,7/7, color = "black", alpha = 1)
    ax.axvspan(3,7,0/7,1/7, color = "black", alpha = 1)

    base_date = datetime.date(2000, 1, 1)

    # 月の描画
    for i in range(6):
        nm = base_date + relativedelta(months=i)
        m = nm.strftime('%b')
        a = 1 if dt.month == nm.month else 0.2
        ax.text(0.5+i, 6.5, m, fontsize=16,
                            verticalalignment="center",
                            horizontalalignment="center",
                            alpha = a)
    for i in range(6):
        nm = base_date + relativedelta(months=6+i)
        m = nm.strftime('%b')
        a = 1 if dt.month == nm.month else 0.2
        ax.text(0.5+i, 5.5, m, fontsize=16,
                            verticalalignment="center",
                            horizontalalignment="center",
                            alpha = a)
        
    # 日の描画
    for i in range(31):
        a = 1 if i < calendar.monthrange(dt.year, dt.month)[1] else 0.2
        x = 0.5 + i%7
        y = 0.5 + abs(4-i//7)
        ax.text(x, y, str(i+1), fontsize=16,
                            verticalalignment="center",
                            horizontalalignment="center",
                            alpha = a)
    
    cmap = gen_cmap_rgb([(0.2,0.2,1),(0.8,0.8,1),(1,1,1),(1,0.8,0.8),(1,0.2,0.2)])
    rgb = cmap(np.arange(256))
    for i in range(31):
        if i >= len(l):
            break
        x = i%7
        y = 4 - i//7
        ax.axvspan(x,x+1,y/7,(y+1)/7, color = rgb[l[i]])

for i in range(1, 13):
    dt = datetime.date(2000, i, 1)
    l = list(df[df['date'].dt.month == i]['rank'])
    draw(fig, dt, l)

おわりに

最初1パターン見つけるのに数時間かかったときは、すべての日付の全パターンを数え上げるなんて、私の力じゃ到底無理なんじゃないかと半ば諦めていました。
ただ、少しの工夫でぐんぐん探索時間が減って、アルゴリズムって素晴らしいなと改めて実感しました。
まだまだ工夫をすれば探索時間を短縮する余地はあると思います。もし、もっと効率的な探索の方法が思いついた方はコメントでご教示いただけるとありがたいです！

これからも毎日「A-Puzzle-A-Day」で遊びつつ、次は数独を解くプログラムに挑戦してみたいと思います。

参考記事

A Puzzle A Day のソルバーを書いてみた
毎日のパズルで禿げ散らかしそうになった時に
Colormap カラーマップ
PythonでのUnion-Find（素集合データ構造）の実装と使い方