事の発端
モンテカルロ法を使って円周率を計算してみようという宿題をもらいました。
円周率...3.14でなんか計算に使うやつ程度の認識しかない...![]()
早速やっていきます。
調べる
登場人物はモンテカルロ法と円周率の2つだけですが、全く見当もつかないので調べてみます。
モンテカルロ法
モンテカルロ法(モンテカルロほう、(英: Monte Carlo method、MC)とはシミュレーションや数値計算を乱数を用いて行う手法の総称。元々は、中性子が物質中を動き回る様子を探るためにスタニスワフ・ウラムが考案しジョン・フォン・ノイマンにより命名された手法。カジノで有名な国家モナコ公国の4つの地区(カルティ)の1つであるモンテカルロから名付けられた。ランダム法とも呼ばれる。
https://ja.wikipedia.org/wiki/%E3%83%A2%E3%83%B3%E3%83%86%E3%82%AB%E3%83%AB%E3%83%AD%E6%B3%95
ふむふむ ![]()
計算理論の分野において、モンテカルロ法とは誤答する確率の上界が与えられる乱択アルゴリズム(ランダム・アルゴリズム)と定義される[1]。一例として素数判定問題におけるミラー-ラビン素数判定法がある。このアルゴリズムは与えられた数値が素数の場合は確実に Yes と答えるが、合成数の場合は非常に少ない確率ではあるが No と答えるべきところを Yes と答える場合がある。一般にモンテカルロ法は独立な乱択を用いて繰り返し、実行時間を犠牲にすれば誤答する確率をいくらでも小さくすることができる。またモンテカルロ法の中でも任意の入力に対して最大時間計算量の上界が入力サイズの多項式で与えられるものを効率的モンテカルロ法という[2]。
続きを読んだところ、あまりにもわからなすぎて読むことへの抵抗感が湧き上がってきました。
wiki以外を見てみます。
1. 1×1 の正方形内にランダムに点を打つ
2. 原点(左下の頂点)から距離が 1 以下なら 1 ポイント, 1 より大きいなら 0 ポイント追加
3. 以上の操作を N 回繰り返す,総獲得ポイントを X とするとき, 4X/Nが円周率の近似値となる
引用: https://manabitimes.jp/math/1182
いくつかのサイトをみましたが上記のサイトが一番優しくてわかりやすい気がします ![]()
プログラムを書いてみる
何を使おう
環境
Jupyter使ってみようと思います。
JupyterLabとJupyter Notebookがあります。一体何が違うか調べてみます。 ![]()
以下、stackoverflowより引用
Jupyter Notebook
Jupyterノートブック文書を作成するためのWebベースの対話型計算環境である。Python (IPython)、Julia、Rなどの言語をサポートし、データ解析、データ可視化、さらにインタラクティブな探索的コンピューティングに大きく利用されています。
JupyterLab
ノートブックを含む次世代のユーザーインターフェイスです。モジュール構造を持ち、複数のノートブックやファイル(HTML、Text、Markdownsなど)を同じウィンドウ内でタブとして開くことができます。よりIDEに近い体験を提供します。
今回はJupyterLabをブラウザで使用します。
Try it in your browser からいけます。
ライブラリを呼び出す
ファイルは左上からNotebookを新規作成しました。
描画に必要なライブラリを呼び出します。
import matplotlib.pyplot as plt
import numpy as np
タブの下のいくつかマークがある中に、再生マーク(右三角)があります。それを押すと、次の書くところが出ます。(画像だと[3]:となっているところ)
先に書いた内容は次に引き継がれるようです。consoleみたいな感じなのかな。
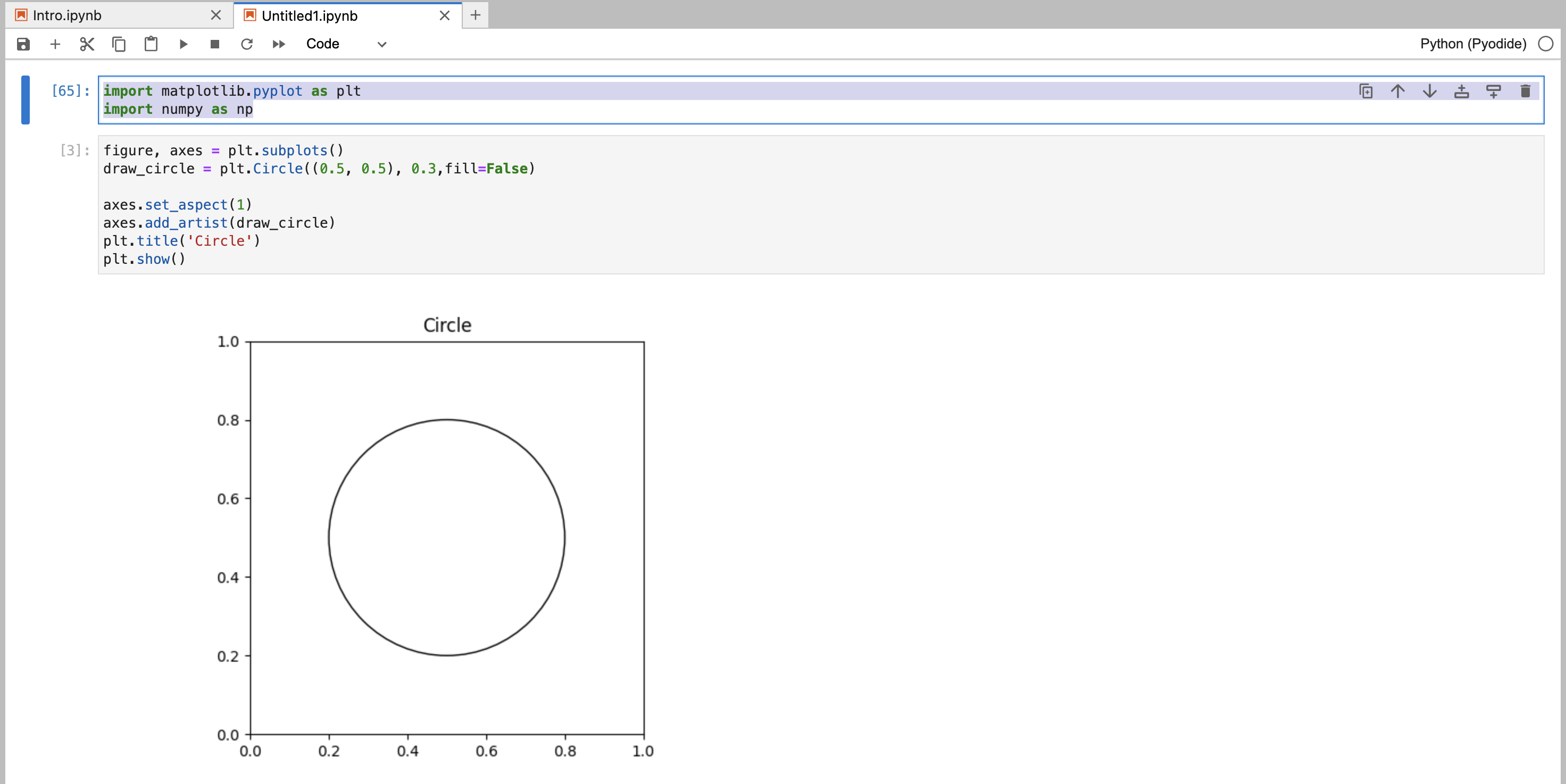
円を描画
円の書き方は色々あるようです。 参考にした外部サイト
ちょっと円の大きさを直します。
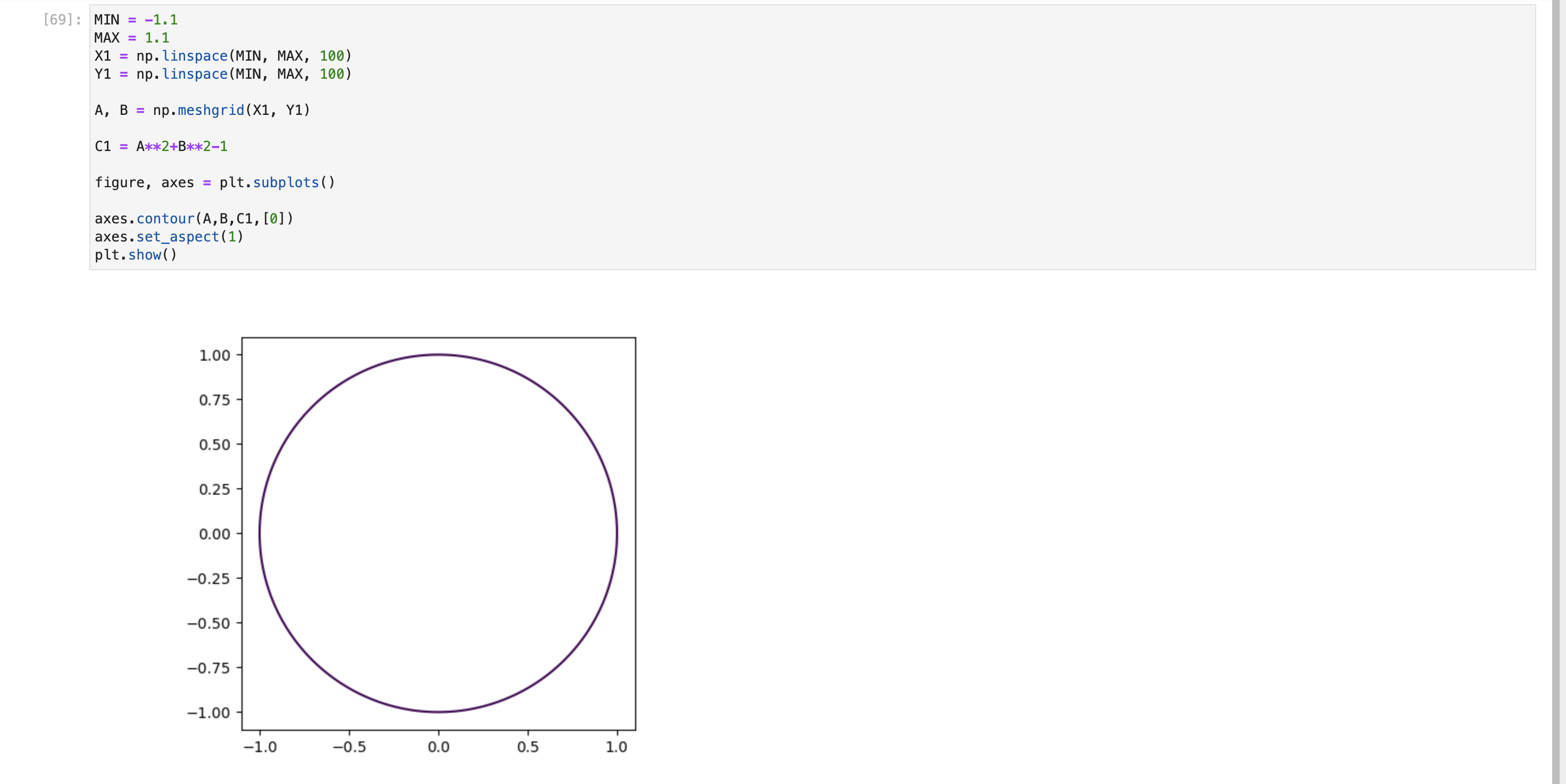
点を描画
この時点ではこんな感じです。
# 枠の描画
MIN = -1.1
MAX = 1.1
X1 = np.linspace(MIN, MAX)
Y1 = np.linspace(MIN, MAX)
A, B = np.meshgrid(X1, Y1)
# 円の描画
C1 = A**2+B**2-1
figure, axes = plt.subplots()
axes.contour(A,B,C1,[0])
axes.set_aspect(1)
# 点の描画
N = 250
X2 = np.random.rand(N)
Y2 = np.random.rand(N)
plt.scatter(X2, Y2, marker="^")
plt.show()
原点からの距離を計算したい。
原点からの距離の計算
色々調べたところ numpy.linalg.norm が良さそうです。(2点間の距離のことなどをノルムと言うらしい)
# 点の描画
N = 250
X2 = np.random.rand(N)
Y2 = np.random.rand(N)
+ C2 = list(map(lambda x, y: np.linalg.norm([x,y]), X2,Y2))
+ plt.scatter(X2, Y2, c=C2, marker="^")
- plt.scatter(X2, Y2, marker="^")
plt.show()

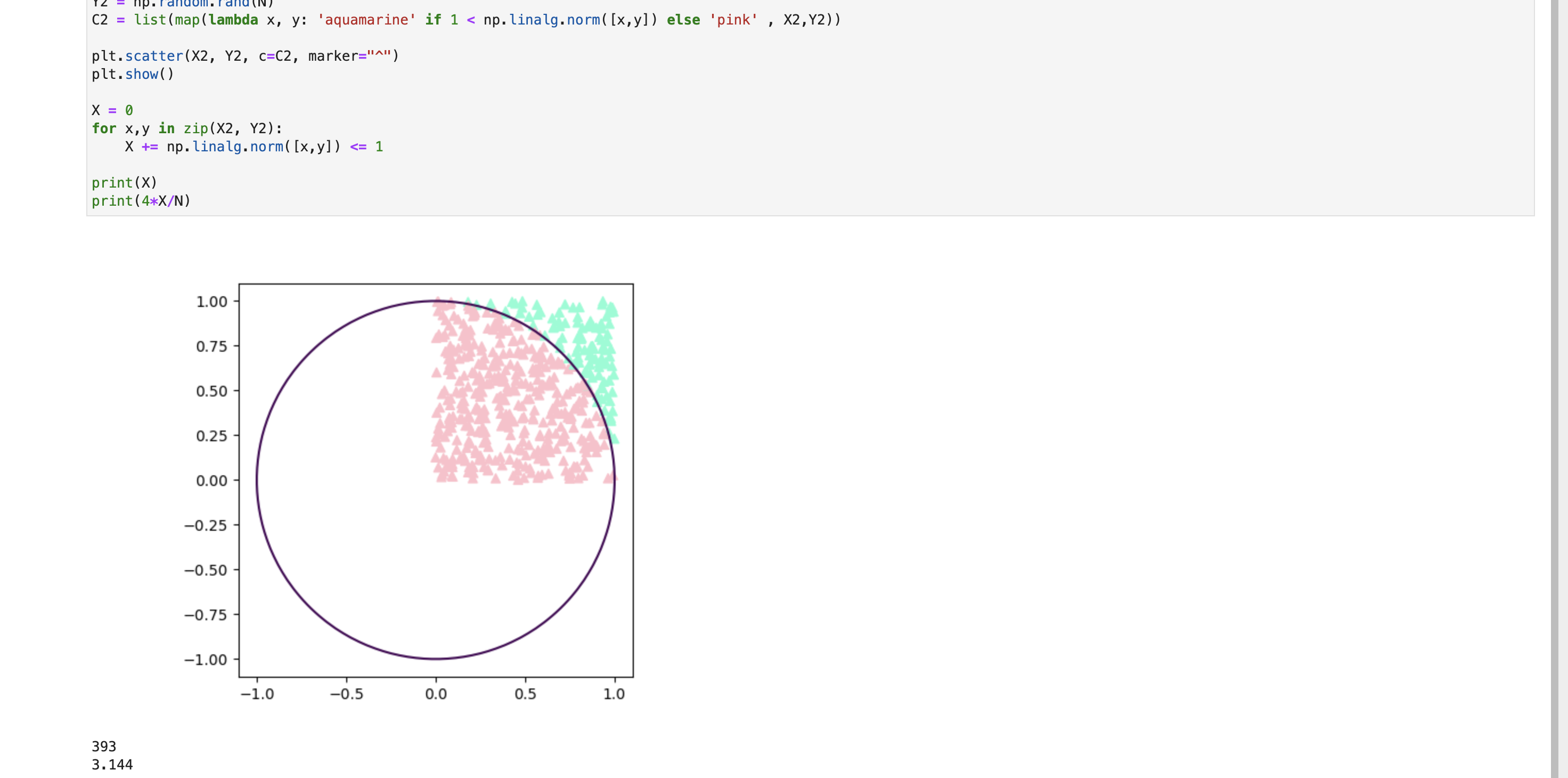
ちょっと想像してた結果と違いました。距離が1以下と1より大きい場合で色を分けたい。
# 点の描画
N = 250
X2 = np.random.rand(N)
Y2 = np.random.rand(N)
- C2 = list(map(lambda x, y: np.linalg.norm([x,y]), X2,Y2))
+ C2 = list(map(lambda x, y: 'aquamarine' if 1 < np.linalg.norm([x,y]) else 'pink' , X2,Y2))
plt.scatter(X2, Y2, c=C2, marker="^")
plt.show()
計算する
1. 1×1 の正方形内にランダムに点を打つ
2. 原点(左下の頂点)から距離が 1 以下なら 1 ポイント, 1 より大きいなら 0 ポイント追加
3. 以上の操作を N 回繰り返す,総獲得ポイントを X とするとき, 4X/Nが円周率の近似値となる
元々はこんな話でした。
# 点の描画
N = 250
X2 = np.random.rand(N)
Y2 = np.random.rand(N)
C2 = list(map(lambda x, y: 'aquamarine' if 1 < np.linalg.norm([x,y]) else 'pink' , X2,Y2))
plt.scatter(X2, Y2, c=C2, marker="^")
- plt.show()
+ # plt.show()
+
+ X = 0
+ for x,y in zip(X2, Y2):
+ X += np.linalg.norm([x,y]) <= 1
+
+ print(X)
+ print(4*X/N)
書いてみました。グラフの描画は要らないのでコメントアウトします。

近似値=3.152 ![]()
Nを500に増やしてみました。
近似値=3.144 ![]()
最終系
N = 15000
def calc_maybe_pi():
X2 = np.random.rand(N)
Y2 = np.random.rand(N)
X = 0
for x,y in zip(X2, Y2):
X += np.linalg.norm([x,y]) <= 1
print(4*X/N)
for i in range(15):
calc_maybe_pi()
余計なコードを削いでみました。
π = 3.14159 26535 89793 23846 26433 83279 50288 …
https://ja.wikipedia.org/wiki/%E5%86%86%E5%91%A8%E7%8E%87
3.1421333333333332が2回出たのでこれでいいことにならないかなぁ ![]()
感想
最近、勉強することがたくさんありすぎて生涯暇することはなさそうだなと思ってます。
知見がないので大変でしたが、またTRYしたいと思います。


