1. はじめに
前回に引き続き、ベイズ初学者である自分がPRMLについて学習したことについてまとめていきたいと思います。
今回の2章は確率分布についての章だったのですが100%飲み込めきれてない箇所などがあるままで記事を書くので間違いがあればご指摘いただけると幸いです。
2. 確率分布
2章では確率分布について取り扱っていきます。
ベイズ推論において、各種確率分布の特徴や性質を知ることは今後のモデル作成の段階で重要です。
複雑なモデルの構成要素である単純なモデルについて学習することでベイズ推論における重要な統計的概念について学ぶことがこの章の目的です。
また、この章の内容については他の投稿である程度触っているので内容としては被る点があるので一部省略していきたいと思います。
以下の内容について述べていきます。
・2.4 指数型分布族
・2.5 ノンパラメトリック法
この後の演習問題につきましては、自分も解いている最中な上に答えは他の方が書いているので省略していきます。
2.4 指数型分布族
混合ガウス分布を除いて、PRMLで述べられている確率分布ではこの指数型分布族が紹介されています。
以下式で表される指数型分布族は共通している性質を持つことで知られている。
$$
p(\mathbf{x}\ |\ \mathbf{η}) =
h(\mathbf{x})g(\mathbf{η})
exp\big\lbrace \mathbf{η}^T\mathbf{u}(\mathbf{x}) \big\rbrace d\mathbf{x} \tag{1}\\
[\mathbf{η}:自然パラメータ, \mathbf{u}(\mathbf{x}):\mathbf{x}の任意の関数]
$$
$g(\mathbf{η})$は分布を正規化するための係数と解釈できるため以下の条件を満たす。
$$
g(\mathbf{η})\int{h(\mathbf{x})
exp\big\lbrace \mathbf{η}^T\mathbf{u}(\mathbf{x}) \big\rbrace d\mathbf{x}} = 1
$$
これは連続型変数を想定している時の式なので、離散型変数の場合は積分を総和に置き換えます。
PRMLでは三種類の確率分布を指数型分布族の標準系に変形する計算が書かれていますが、かなり長くなrるので割愛します。
2.4.1 最尤推定と十分統計量
- 最尤推定による(1)式におけるパラメーラベクトル$\mathbf{\eta}$の推定を考えていきます。
まず(1)式において$\mathbf{\eta}$についての両辺の勾配を求めます。
$$
\nabla g(\mathbf{\eta}) \int h(\mathbf{x})
exp\big\lbrace \mathbf{\eta}^T \mathbf{u}(\mathbf{x}) \big\rbrace d\mathbf{x} +g(\mathbf{\eta}) \int h(\mathbf{x})
exp\big\lbrace \mathbf{\eta}^T \mathbf{u}(\mathbf{x}) \big\rbrace
\mathbf{u}(\mathbf{x}) d\mathbf{x} = 0
$$
この式を変形させて以下式のような$g(\eta)$に関する等式が得られる。
$$
-\frac{\nabla g(\eta)}{g(\eta)} =
g(\mathbf{\eta}) \int h(\mathbf{x})
exp\big\lbrace \mathbf{\eta}^T \mathbf{u}(\mathbf{x}) \big\rbrace \mathbf{u}(\mathbf{x}) d\mathbf{x}
$$
ここで(1)式を上式に代入すると、分布の正規をするための係数を用いることで分布自体の期待値を算出できることが示されます。
$$
\begin{aligned}
-\nabla \ln g(\eta)
&= \int p(\mathbf{x}\ |\ \eta)\mathbf{u}(\mathbf{x})d\mathbf{x} \\
&= \mathbb{E}[\mathbf{u}(\mathbf{x})]
\end{aligned}
$$
続いて独立に同じ分布に従うデータの集合$\mathbf{X} = \lbrace \mathbf{x}_1, \cdots , \mathbf{x}_N \rbrace$について考えていきます。
この集合に対する尤度関数は以下のようになります。
$$
p(\mathbf{x}\ |\ \mathbf{η}) =
\prod _{n = 1}^{N} h(\mathbf{x}_n)g(\mathbf{η})^N
exp\bigg\lbrace \mathbf{η}^T\sum _{n = 1}^{N}\mathbf{u}(\mathbf{x}) \bigg\rbrace d\mathbf{x}\\
$$
この尤度関数の対数を求め、$\eta$について勾配を0とすると最尤推定量$\eta _{ML}$が満たすべきいか式のような条件が得られる。
$$
\nabla \ln g(\eta _{ML})= \frac{1}{N} \sum _{n = 1}^{N}\mathbf{u}(\mathbf{x}_n) \tag{2}
$$
(2)式を解くことで$\eta _{ML}$を得ることができます。
また、(2)式より$\eta$の最尤推定量は$\displaystyle \sum _{n = 1}^{N}\mathbf{u}(\mathbf{x}_n)$に依存することがわかります。
よって$\displaystyle \sum _{n = 1}^{N}\mathbf{u}(\mathbf{x}_n)$は分布の十分統計量と呼ばれます。
2.4.2 共役事前分布
ここについては、他の記事でも書いてあるので省略します。
簡単にいうと、設定した事前分布と観測データを得られた後に求められる事後分布が同じ関数形になるような事前分布のことです。
2.4.3 無情報事前分布
事前分布を導入するメリットとして、解決したい課題に対して事前に知識を持っている時その知識をモデルに反映できる点が挙げられます。
しかし実際に問題を解決する際には、事前知識がない場合も多くあり、そのような時には普通の事前分布を設定するのではなく事後分布に対する影響をなるべく小さくした無情報事前分布を求める手法を取ります。そのため「データ自身に語らせる」と象徴づけられます。
ex) 一様分布(無情報事前分布)と逆ガンマ関数(弱情報事前分布)を用いたときの比較
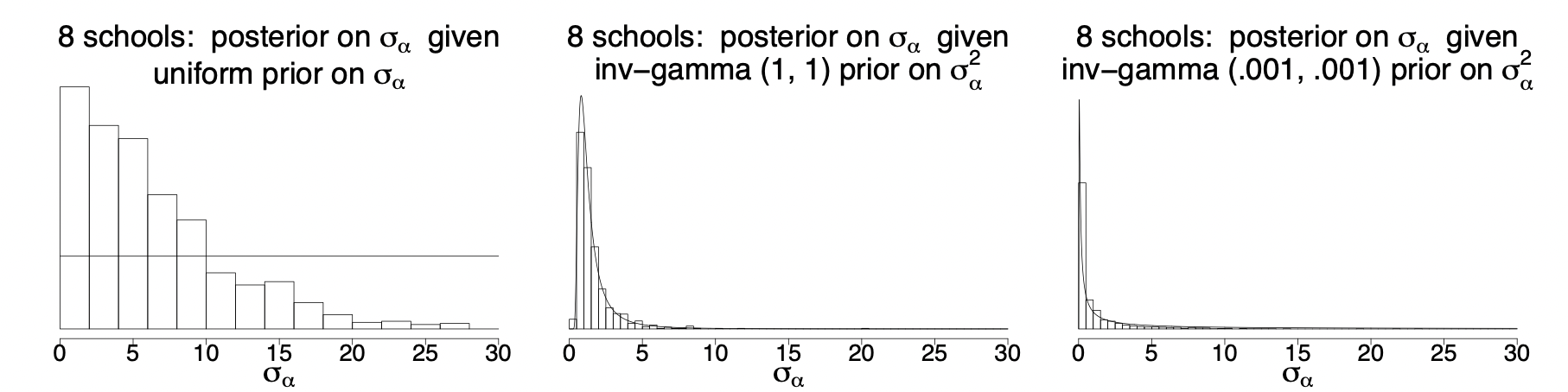図1) [1]より引用した階層ベイズにおける事後分布の比較
【無情報事前分布を連続値の事前分布とするときの問題】
離散地の場合は、パラメータが取り得る状態の個数の逆数を用いるだけで良いが、
連続値においては二つの潜在的な問題点があります。
-
事前分布が正しく正規化されない場合があること
→これはパラメータλの定義域が有界でない時に$\lambda$上での積分が発散することに由来します。※このような正則化できない事前分布を変則事前分布といいます。
-
変数を非線形変換したときに、変換後の変数の確率密度が定数とは限らないこと
2.5 ノンパラメトリック法
これまで考えてきた確率密度の利用法は少数のパラメータで関数形が決まるパラメトリックなアプローチと呼ばれています。
【パラメトリックなアプローチの重大な制限】
パラメトリックなアプローチにおいて、
「選んだ密度関数がデータを生成した分布を表現するのに貧弱なモデルである可能性がある」という制限があります。
この制限によって予測性能の低下に繋がります。
この対策としてはノンパラメトリックなアプローチと呼ばれる分布の形状に対してわずかな仮定しか置かない手法を用います。
PRMLではベイズ主義的な手法ではなく、頻度主義的手法の中でも多用されている
- カーネル推定法
- 最近傍法
を解説しています。
2.5.1 カーネル密度推定法
ある$D$次元のユークリッド空間中の未知の確率密度$p(\mathbf{x})$から観測値の集合が得られていて、ここから$p(\mathbf{x})$の値を推定する問題を考えます。
カーネル法においては確率密度を求めたいデータ点を$\mathbf{x}$とし、この点を中心とする超立方体を領域$R$とします。
このとき以下のような関数を用いることで領域内の点の個数$K$を数えるのに便利です。
$$
\begin{eqnarray}
k(\mathbf{u}) =
\begin{cases}
1 & |u_i| \geqq \frac{1}{2} \ [i = 1,\dots , D] \\
0 & other
\end{cases}
\end{eqnarray}\tag{3}
$$
※この関数は原点を中心とする単位立方体を表し、カーネル関数の一例です。
この関数をもとにして$K$は以下式を計算することで求めることができます。
$$
K = \sum_{n = 1}^{N}k\bigg(\frac{\mathbf{x}-\mathbf{x_n}}{h}\bigg)\\
[h:\mathbf{x}を中心とする立方体の一辺の長さ] \tag{4}
$$
ここでデータ集合における観測値の個数を$N$、領域$R$の体積を$V$とすると確率密度$p(\mathbf{x})$の密度推定量は以下式で表されます。
$$
p(\mathbf{x}) = \frac{K}{NV} \tag{5}
$$
(5)式に(4)式を代入することで$\mathbf{x}$の推定密度が得られます。
$$
p(\mathbf{x}) = \frac{1}{N}\sum_{n = 1}^{N}
\frac{1}{h^D}k\bigg(\frac{\mathbf{x}-\mathbf{x_n}}{h}\bigg)\tag{6}\\
*V = h^Dを用いた。
$$
(6)式の解釈を(3)の関数の持つ対称性を用いると、
$\mathbf{x}$を中心とする立方体が一つあるのではなく中心があるデータ点$x_n$にある$N$個の立方体の総和を取ったとみることができ、それに伴って問題点が生じます。
立方体が複数あることで、各立方体の縁で人為的な不連続が生じてしまいます。
この問題に対してはより滑らかなカーネル関数を用いることで対処します。
一般的にカーネル関数としてガウスカーネルが用いられ確率密度モデルは以下式のようになります。
$$
p(\mathbf{x}) = \frac{1}{N}\sum_{n =1}^{N}
\frac{1}{(2\pi h^2)^{D/2}}
\exp\bigg\lbrace -\frac{||\mathbf{x}-\mathbf{x_n}||^2}{2h^2} \bigg\rbrace \tag{7}\\
[h:ガウス分布の標準偏差]
$$
この式においてパラメータ$h$は平滑化パラメータの役割を持っており、小さすぎず大きすぎない最適な$h$を求める必要があります。
【カーネル密度推定法のメリットとデメリット】
<メリット>
- 「訓練」段階において必要な作業が訓練集合の保存だけなので、訓練段階における計算をしなくて済む。
<デメリット>
- 求めた確率密度の評価にかかる計算コストがデータ集合の大きさに比例する。
- カーネル幅を決めるパラメータhが全てのカーネルで一定であるため、hが大きすぎる時データの特徴を見逃したり、反対に小さすぎた時は密度が低い領域においてノイズの多い推定をしてしまう。
2.5.2 最近傍法
デメリットの二つ目であるように、カーネルの幅を決めるパラメータであるhを最も適切に設定するためにはデータ空間内の位置に応じて、hを変えるべきだと分かります。
この考えを実際に行なっているのが最近傍法による密度推定です。
[K近傍法]
◇確率密度$p(\mathbf{x})$を推定したい点$\mathbf{x}$を中心としてなる小球を考えていく。
またこの時領域$\mathcal{R}$内のデータ点の個数$K$を固定し、領域の体積を求めていく。
この時、確率密度は以下式で表すことができます。
$$
p(x) = \frac{K}{NV}
$$
K近傍法で生成されるモデルは、
- ここでこのK近傍法をクラス分類問題への拡張を考えていきます。
< 手順 >
K近傍法を各クラスごとに適用し、ベイズの定理を適用する。
各クラスの密度の推定値$p(\mathbf{x}\ |\ \mathcal{C}_k)$は以下式で表すことができます。
$$
p(\mathbf{x}\ |\ \mathcal{C}_k) = \frac{K_k}{N_kV} \tag{8}
$$
同様にデータの密度$p(\mathbf{x})$は以下式で表すことができます。
$$
p(\mathbf{x}) = \frac{K}{NV} \tag{9}
$$
次に、各クラスの事前分布$p(\mathcal{C_k})$は以下式で表すことができます。
$$
p(\mathcal{C_k}) = \frac{N_k}{N} \tag{10}
$$
(8), (9), (10)式を用いてベイズの定理を適用させるとクラスに関する事後分布$p(\mathcal{C}_k\ |\ \mathbf{x})$を得ることができます。
$$
\begin{align}
p(\mathcal{C}_k\ |\ \mathbf{x}) &=
\frac{p(\mathbf{x}\ |\ \mathcal{C}_k)p(\mathcal{C_k})}{p(\mathbf{x})} \\
&=\frac{K_k}{K} \tag{11}
\end{align}
$$
よって誤分類の確率を最小化するためには(11)式の値を最大化するためのクラスにテスト点$\mathbf {x}$を割り当てることと同義であることが分かります。
ここで新しいデータ点を分類する時を考えると、訓練データ集合の中でも最も多数派のクラスに新たな点を割り当てることで分類誤差の少ない分類が可能となります。
＊また、(11)式において$K= 1$の時のK近傍法によるクラス分類手法を最近傍法と言います。
カーネル密度推定法においてもK近傍法においてもデータ全体を保持する必要があるため、データ集合が大きい時計算量が膨大になるというデメリットがある。
3. まとめ
今回はPRMLの二章の後半部分についてまとめました。
ゆっくり記事を書いていたらインプットの速度に追いつかなくなったのでまたこれから記事の作成に尽力していきます。
4. 参考資料
[1]Andrew Gelman "Prior distributions for variance parameters in
hierarchical models" ISBA 2006
[2]パターン認識と機械学習 上 ベイズ理論による統計的予測