ベイズ機械学習における学習の事後分布の推移 ~多次元Gaussian分布~

1. はじめに

• 今回はベイズ機械学習における多次元ガウス分布の学習による事後分布の推移をPythonを用いて可視化していきます。
• 前回の記事同様しょこさんが書かれているからっぽのしょこというブログを参考に作成しました。
• 多次元ガウス分布においてパラメータの推定を行う際は「平均が未知の時、精度行列が未知の時、両方とも未知の時」この3パターンに分けられるのでそれぞれについて考えていきます。
• また、今回も前回同様に可視化を目的とするので計算の詳細部分については省略します。
  詳しくは先述したブログを参照してください。

2. 平均が未知の時における学習

$D$次元の確率変数である$\mathbf{x} \in \mathbb{R}^Dの $平均パラメータである$\boldsymbol{\mu}$のみが未知で精度行列$\mathbf{\Lambda}$が既知の時について考えていきます。
すなわち、今回考える観測モデルとしては以下式のようになり、その平均パラメータである$\boldsymbol{\mu}$の共役事前分布にはガウス事前分布を用いる。
$$
p(\mathbf{x}\ |\ \boldsymbol{\mu} ) =
\mathcal{N}(\mathbf{x}\ |\ \boldsymbol{\mu}, \mathbf{\Lambda^{-1}})
$$

[事前分布]

$$
p(\boldsymbol{\mu}) =
\mathcal{N}(\boldsymbol{\mu}|
\boldsymbol{m}, \mathbf{\Lambda}_\boldsymbol{\mu}^{-1}) \\
[\boldsymbol{m}\in\mathbb{R}^D, \mathbf{\Lambda}_\boldsymbol{\mu}^{-1}\in\mathbb{R}^{D×D}:ハイパーパラメータ]
$$

$N$個のデータ$\mathbf{X}=\lbrace{\mathbf{x}_1,\dots, \mathbf{x}_N}\rbrace$を観測した後の事後分布は以下式のようになる。

[事後分布]

$$
p(\boldsymbol{\mu}\ |\ \mathbf{X}) =
\mathcal{N}(\boldsymbol{\mu}|\hat{\boldsymbol{m}}, \hat{\mathbf{\Lambda}_\boldsymbol{\mu}}^{-1}) \\
\left[
\begin{array}{l}
\hat{\boldsymbol{m}} =
\hat{\mathbf{\Lambda}_\boldsymbol{\mu}}^{-1}
(\mathbf{\Lambda}{\displaystyle \sum_{n = 1}^{N}}{\mathbf{x_n}}
+\mathbf{\Lambda}_\boldsymbol{\mu}\mathbf{m}) \\
\hat{\mathbf{\Lambda}_\boldsymbol{\mu}} = N\mathbf{\Lambda}+\mathbf{\Lambda}_\boldsymbol{\mu}
\end{array}
\right]
$$

• この更新をNの値の変化に伴う事後分布の推移として捉えて作成したアニメーション
  

3. 精度行列が未知の時における学習

次は、平均パラメータが既知とした時に精度行列$\Lambda$の分布に関する確率分布を知りたい時について考えていく。
この時における観測モデルは以下のようになる。
$$
p(\mathbf{x}\ |\ \boldsymbol{\mu} ) =
\mathcal{N}(\mathbf{x}\ |\ \boldsymbol{\mu}, \mathbf{\Lambda^{-1}})
$$

また、精度行列の共役事前分布としては、$D×D$の正定値行列を生成する確率分布であるウィシャート事前分布が用いられる。

[事前分布]

$$
p(\mathbf{\Lambda}) =
\mathcal{W}(\mathbf{\Lambda}\ |\ \nu, \mathbf{W}) \\
\left[
\begin{array}{l}
\nu>D-1の実数値 \\
\mathbf{W}:D×Dの正定値行列　
　　　
\end{array}
\right]
$$
先ほどと同様に、$N$個のデータ $\mathbf{X}=\lbrace{\mathbf{x}_1,\dots, \mathbf{x}_N}\rbrace$を観測したときの事後分布について考える。

[事後分布]

$$
p(\mathbf{\Lambda}\ |\ \mathbf{X}) =
\mathcal{W}(\mathbf{\Lambda}\ |\ \hat{\nu}\ , \hat{\mathbf{W}}\ ) \\
\left[
\begin{array}{l}
\hat{\nu} = N + \nu\\
\hat{\mathbf{W}^{-1}} =
\displaystyle \sum_{n = 1}^{N}(\mathbf{x}_n-\boldsymbol{\mu})(\mathbf{x}_n-\boldsymbol{\mu})^T+\mathbf{W}^{-1}　
　　　
\end{array}
\right]
$$

• この更新をNの値の変化に伴う事後分布の推移として捉えて作成したアニメーション
  (今回はウィシャート分布の直接的な推移の様子がかなり分かりにくかったのと自分の現状の知識では綺麗にプロットできないと判断したためしょこさん同様に視覚的に分かりやすい事後分布をもとに予測データを作りその様子の推移でアニメーションを作成した。)
  

4. 平均、精度行列ともに未知の時

最後に平均、精度行列がともに未知の時について考えていきます。
その時における観測モデルは以下式のようになります。
$$
p(\mathbf{x}\ |\ \boldsymbol{\mu}, \mathbf{\Lambda} ) =
\mathcal{N}(\mathbf{x}\ |\ \boldsymbol{\mu}, \mathbf{\Lambda^{-1}})
$$

多次元ガウス分布において平均、精度が共に未知の時に共役事前分布としてガウス分布とウィシャート分布を組み合わせたガウス・ウィシャート分布を用いる。

[事前分布]

$$
\begin{align}
p(\boldsymbol{\mu}, \mathbf{\Lambda}) &=
NW(\boldsymbol{\mu}, \mathbf{\Lambda}\ |\ \mathbf{m}, \beta, \nu, \mathbf{W}) \\
&=\mathcal{N}(\boldsymbol{\mu}|\boldsymbol{m}, (\beta\mathbf{\Lambda})^{-1})
\mathcal{W}(\mathbf{\Lambda}\ |\ \nu, \mathbf{W}) \\
&[\mathbf{m}, \beta, \nu, \mathbf{W}:ハイパーパラメータ]
\end{align}
$$

これまでと同様に観測データ$\mathbf{X}が与えられときの事後分布を考える。

[事後分布]

$$
p(\boldsymbol{\mu}, \mathbf{\Lambda}\ |\ \mathbf{X}) =
\frac{p(\mathbf{X}\ |\ \boldsymbol{\mu}, \mathbf{\Lambda})
p(\boldsymbol{\mu}, \mathbf{\Lambda})}
{p(\mathbf{X})}
$$
となり、これは$\boldsymbol{\mu}, \mathbf{\Lambda}$に関する条件付き分布としてみることで以下のように分解できるため、$\boldsymbol{\mu}, \mathbf{\Lambda}$においてそれぞれの事後分布を求める。
$$
p(\boldsymbol{\mu}, \mathbf{\Lambda}\ |\ \mathbf{X})=
p(\boldsymbol{\mu}\ |\ \mathbf{\Lambda}, \mathbf{X})p(\mathbf{\Lambda}\ |\ \mathbf{X})
$$

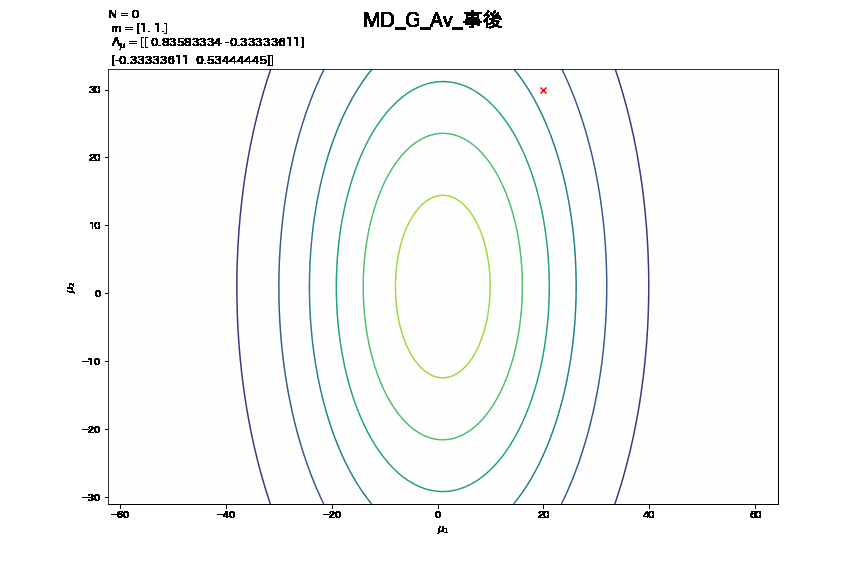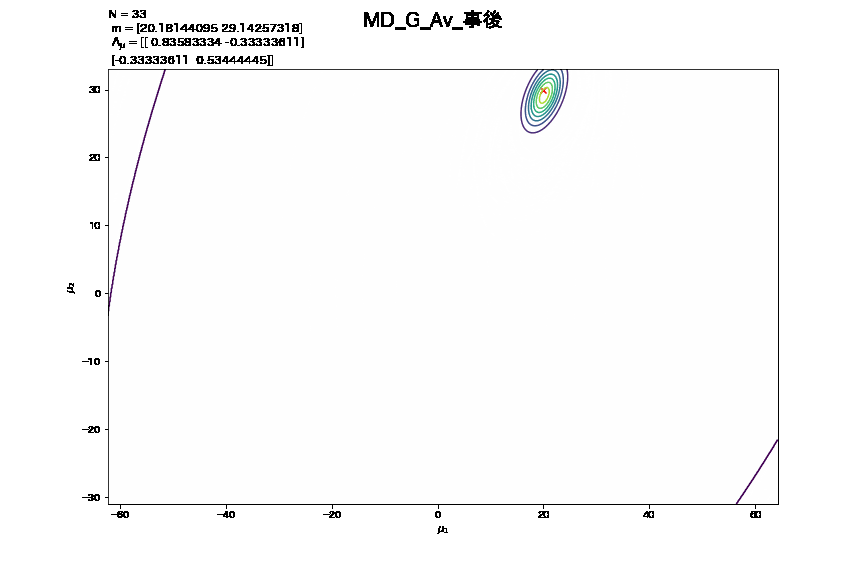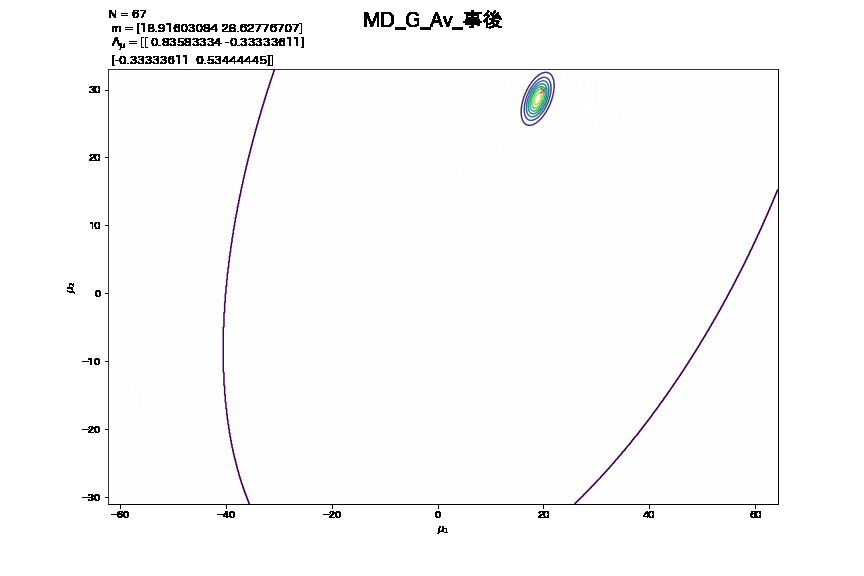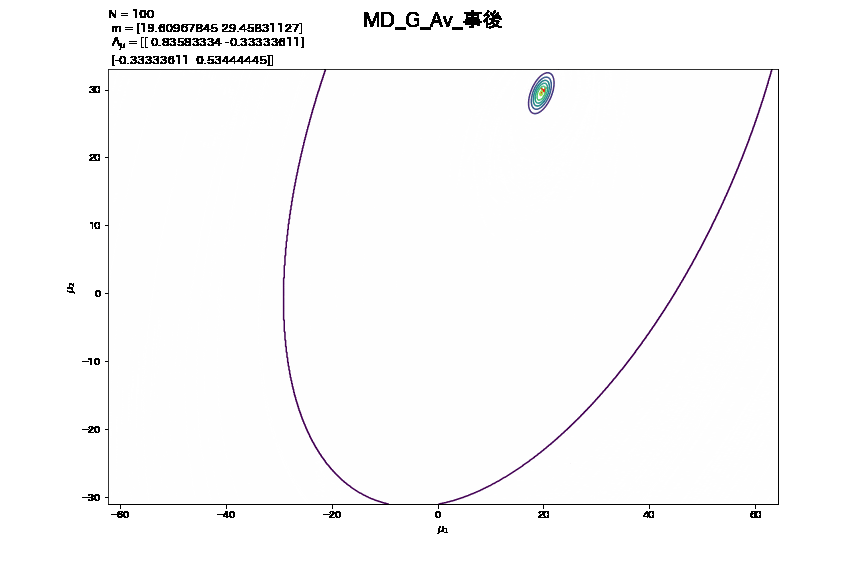
[μの事後分布]

まず$\boldsymbol{\mu}$の事後分布は以下のようになる。
$$
p(\boldsymbol{\mu}\ |\ \mathbf{\Lambda}, \mathbf{X}) =
\mathcal{N}(\boldsymbol{\mu}\ |\ \hat{\boldsymbol{m}}, (\hat{\beta}*\mathbf{\Lambda})^{-1}) \\
\left[
\begin{array}{l}
\hat{\boldsymbol{m}} =
\frac{1}{\hat{\beta}}
({\displaystyle \sum_{n = 1}^{N}}{\mathbf{x_n}}+\beta\mathbf{m}) \\
\hat{\beta} = N+\beta
\end{array}
\right]
$$

• この更新をNの値の変化に伴う事後分布の推移として捉えて作成したアニメーション
  

[Λの事後分布]

$$
p(\mathbf{\Lambda}\ |\ \mathbf{X}) =
\mathcal{W}(\mathbf{\Lambda}\ |\ \hat{\nu}\ , \hat{\mathbf{W}}\ ) \\
\left[
\begin{array}{l}
\hat{\nu} = N + \nu\\
\hat{\mathbf{W}^{-1}} =
\displaystyle \sum_{n = 1}^{N}\mathbf{x}_n\mathbf{x}_n^T+
\beta\mathbf{m}\mathbf{m}^T - \hat{\beta}\hat{\mathbf{m}}\hat{\mathbf{m}}^T\mathbf{W}^{-1}　
　　　
\end{array}
\right]
$$

• この更新をNの値の変化に伴う事後分布の推移として捉えて作成したアニメーション
  (精度が未知の時と同様に事後分布をもとにした予測データの推移でアニメーションを作成した。)
  

5. まとめ

今回は多次元ガウス分布に関する学習過程について数式をコードに落とし、Animationを作成することで理解を深めました。
ただ、今回作成したAnimationのうち、ウィシャート分布を共役事前分布としている場合の推移を直接的に表さず間接的に推移している様子を可視化したので、見やすい形でウィシャート分布の推移している様子をAnimationで作成する方法をご教授いただけると幸いです。　

6. 参考資料

◆ 機械学習スタートアップシリーズ ベイズ推論による機械学習入門
◆ からっぽのしょこ