openFrameworksでFractalを表現してみる

##始めに
今回はフラクタルとカオス理論について少し触れる機会があったのでopenFrameworksでフラクタルを表現してみました.
プロジェクトファイルはこちら->FractalTest

##フラクタルとは
名前の由来は分数を意味するフラクションという言葉から来ており,ハウスドルフ次元が位相次元よりも大きいものを一般にフタクタルと呼びます.(何のことかわからない人はスルーで)
フラクタルの特徴としては自己相似性が挙げられる.

##実装
詳しく説明しているときりがないので実装にいきます.
##シェルピンスキーのギャスケット

フラクタルで調べると一番よく出てくる図形だとと思います.
自己相似的な無限な三角形から出来る図形です.
作りかたは以下の手順
①正三角形を一つ用意する
②三角形の各辺の中点を結ぶ
③出来た三角形を刳り貫き一辺の長さが1/2の正三角形を3つ残す
④残った三角形に対し②,③を繰り返す
⑤実際に無限回実行することは不可能なのである程度の繰り返しで終了する

これをopenFrameworksのMeshを使って作りました.
考え方は以下のよう

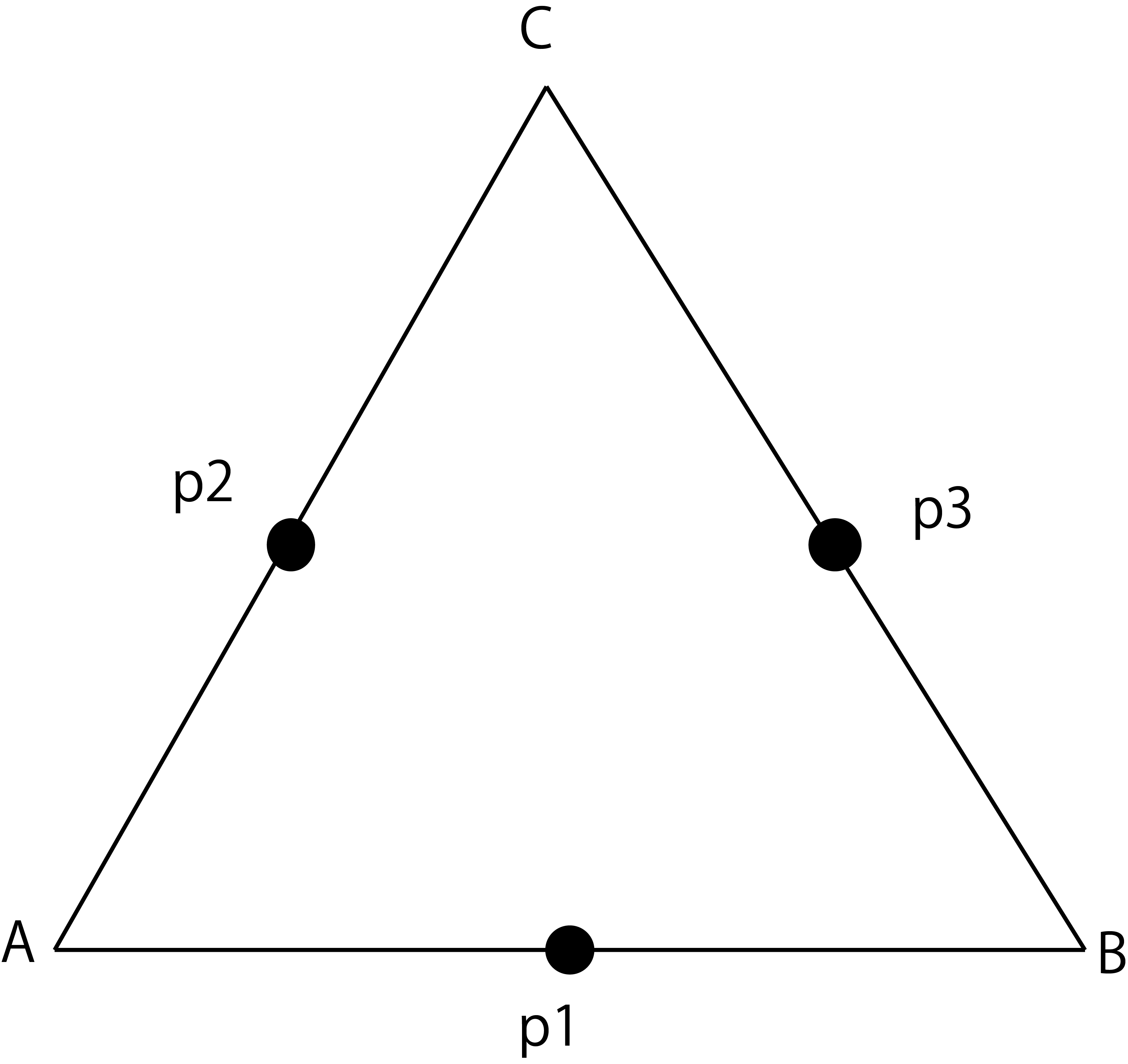
以下の三角形をn回目の切り抜きが終わった三角形の内の一つだとします
各頂点をA,B,Cとし、図のように中点p1,p2,p3を設定します.

ここから新しいMeshのTriangleを三つ作るには
元の三角形ABCを解体して三つの三角形Ap1p2,p1Bp3,p2p3Cを作れば良いわけです.
これを存在する三角形の分だけ繰り返せばn+1回目の作業が終了したことになります.

これをコードで表現したものが以下です

SierpinskiGasket.h

#include "ofMain.h"

class SierpinskiGasket {
public:
    void setup();
    void update();
    void draw();
    void reset();
private:
    int generation = 0; //上記のn
    int frame = 0; //今回は変化を見るために時間経過で三角形を増やす
    int maxGeneration = 8; //最大繰り返し回数
    ofMesh mesh;
};

SierpinskiGasket.cpp

#include "SierpinskiGasket.h"

void SierpinskiGasket::setup(){
    reset();
}

void SierpinskiGasket::update(){
    frame++;
    if(frame % 30 != 0) return;
    if(generation >= maxGeneration) return;
    for(int i = 0; i < 6 * mesh.vertices.size()/3; i++){
        mesh.addColor(ofColor::fromHsb(ofRandom(255), 255, 255)); //各頂点にランダムな色を入れる
    }
    for(int i = mesh.vertices.size() / 3 - 1; i >= 0 ; i--){
        ofPoint p1 = (mesh.getVertices().at(i * 3) + mesh.getVertices().at(i * 3 + 1))/ 2.0;
        ofPoint p2 = (mesh.getVertices().at(i * 3) + mesh.getVertices().at(i * 3 + 2))/ 2.0;
        ofPoint p3 = (mesh.getVertices().at(i * 3 + 1) + mesh.getVertices().at(i * 3 + 2))/ 2.0;
        

		//三角形p2p3C
        mesh.getVertices().insert(mesh.vertices.begin() + i * 3 + 2, p2);
        mesh.getVertices().insert(mesh.vertices.begin() + i * 3 + 2, p3);

        //三角形p1Bp3        
        mesh.getVertices().insert(mesh.vertices.begin() + i * 3 + 1, p1);
        mesh.getVertices().insert(mesh.vertices.begin() + i * 3 + 1, p3);
        
        //三角形Ap1p2
        mesh.getVertices().insert(mesh.vertices.begin() + i * 3 + 1, p1);
        mesh.getVertices().insert(mesh.vertices.begin() + i * 3 + 1, p2);
    }
    generation++;
}

void SierpinskiGasket::draw(){
    ofPushMatrix();
    ofTranslate(ofGetWidth()/2, 50);
    mesh.draw();
    ofPopMatrix();
}

void SierpinskiGasket::reset(){
    generation = 0;
    frame = 0;
    mesh.clear();
    mesh.addVertex(ofPoint(-400, 0));
    mesh.addVertex(ofPoint(400, 0));
    mesh.addVertex(ofPoint(0, 400 * sqrt(3.0)));
    mesh.setMode(OF_PRIMITIVE_TRIANGLES);
    for(int i = 0; i < 3; i++){
        mesh.addColor(ofColor::fromHsb(ofRandom(255), 255, 255));
    }
}

ofApp.cpp

#include "ofApp.h"
#include "SierpinskiGasket.h"

SierpinskiGasket sierpinskiGasket;

void ofApp::setup(){
    ofBackground(0);
    sierpinskiGasket.setup();
}

void ofApp::update(){
    sierpinskiGasket.update();
}

void ofApp::draw(){
    sierpinskiGasket.draw();
}

以上です.

これを実行することによってシェルピンスキーのギャスケットを観測することができます.美しいです.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　↓

##複数個の縮小による自己相似集合
長くなってしまったのでこちらのトピックはソースコードと結果だけ書いておきます.今回の実装について簡潔に説明すると複素平面上の一次の縮小写像f0,f1のを二つ用いて、集合Kに対しK = f0(K)Uf1(K)を満たす集合Kを求めていくプロセスである.詳しく知りたい方は是非カオス理論とフラクタルについて一緒に勉強しましょう.

以下ソースコードです.

ofApp.cpp

#include "ofApp.h"
#include <complex>
//関数のパラメータを定義
complex<double> A = complex<double>(0, 0);
complex<double> B = complex<double>(0.4, 0.5);
complex<double> C = complex<double>(0, 0);
complex<double> D = complex<double>(0.4, -0.5);
//共役を取る
complex<double> getComplexConjugate(complex<double> z){
    return complex<double>(z.real(), - z.imag());
}
//f0
complex<double> f0(complex<double> z){
    return A * z + B * getComplexConjugate(z);
}
//f1
complex<double> f1(complex<double> z){
    return C * (z - 1.0) + D * (getComplexConjugate(z) - 1.0) + 1.0;
}

vector< complex<double> > CSpace;
ofMesh mesh;

void ofApp::setup(){
    ofBackground(0);

    complex<double> z0 = complex<double>(0, 0);
    CSpace.push_back(z0);
    
    for(int i = 0; i < 15; i++){ //15回繰り返せばある程度綺麗
        vector< complex< double> > newCSapce = vector< complex<double> >(0);
        for(int k = 0; k < CSpace.size(); k++){
            newCSapce.push_back(f0(CSpace.at(k)));
            newCSapce.push_back(f1(CSpace.at(k)));
        }
        CSpace = newCSapce;
    }
    for(int i = 0; i < CSpace.size(); i++){
        mesh.addVertex(ofPoint(CSpace.at(i).real() * 400,CSpace.at(i).imag() * 400));
    }
    mesh.setMode(OF_PRIMITIVE_POINTS);
}

void ofApp::draw(){    
    ofPushMatrix();
    ofSetColor(0,255,0);
    ofTranslate(ofGetWidth()/2 - 300, ofGetHeight()/2 );
    mesh.draw();
    ofPopMatrix();
}

たったこれだけのコードでA,B,C,Dの値を変化させることによって以下のような色々な美しい図形が観測できます.

A = 0, B = 0.4 + 0.5i, C = 0, D = 0.4 - 0.5i

A = 0.5 + 0.5i, B = 0, C = 0.5 - 0.5i, D = 0

A = 0.707i, B = 0, C = 0.5, D = 0

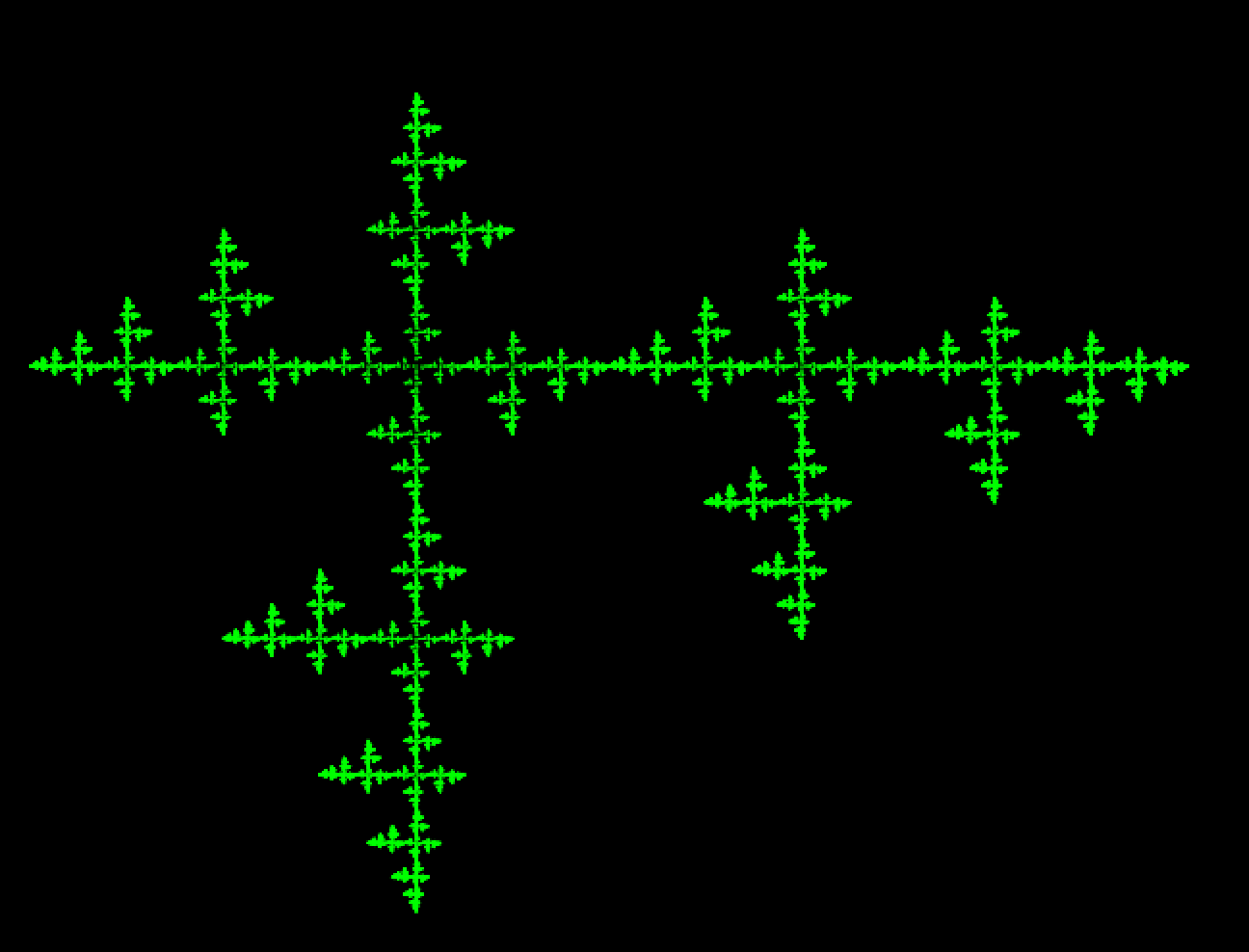
A = 0.4614 + 0.4614i, B = 0, C = 0, D = 0.2896 - 0.585i

##終わりに
今回はフラクタルについて二種類の実装をしてみました.
パラメータを少し変化させるだけで様々な自己相関集合が描けるのはとても興味深いです.
是非一度フラクタルで遊んでみましょう!

2015.12.14