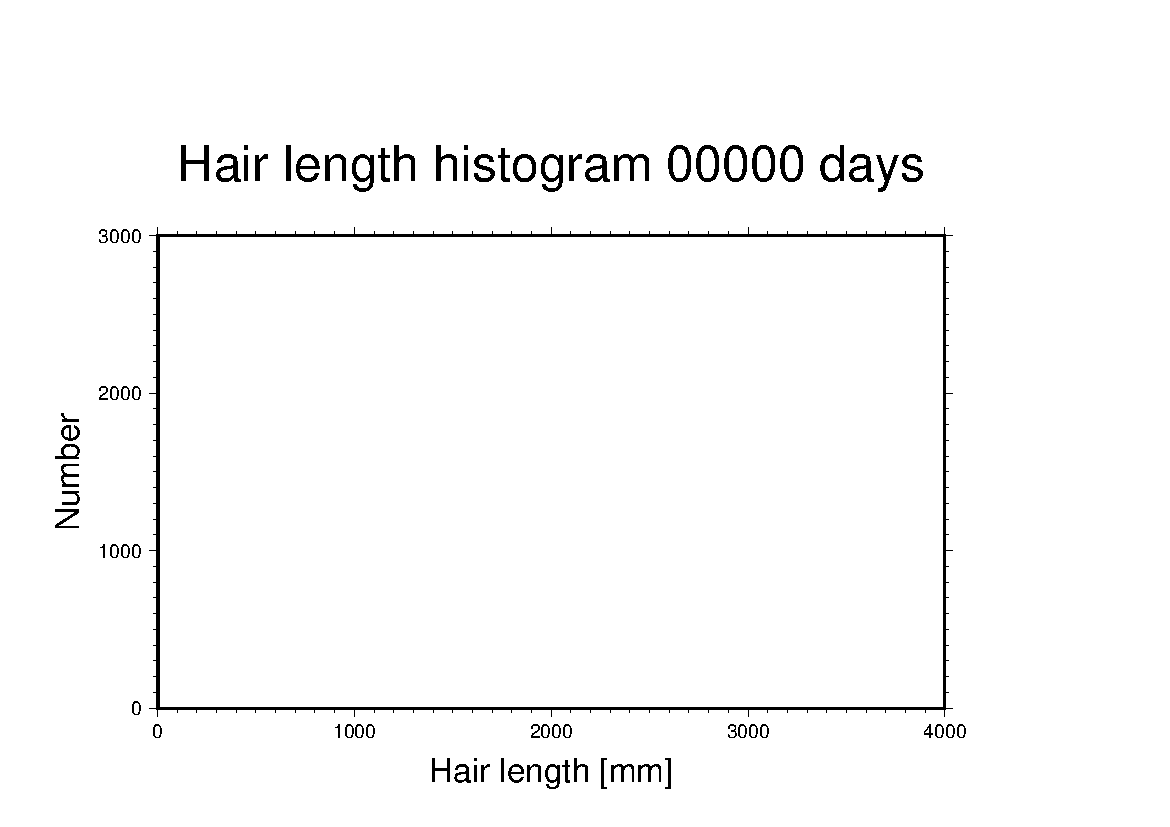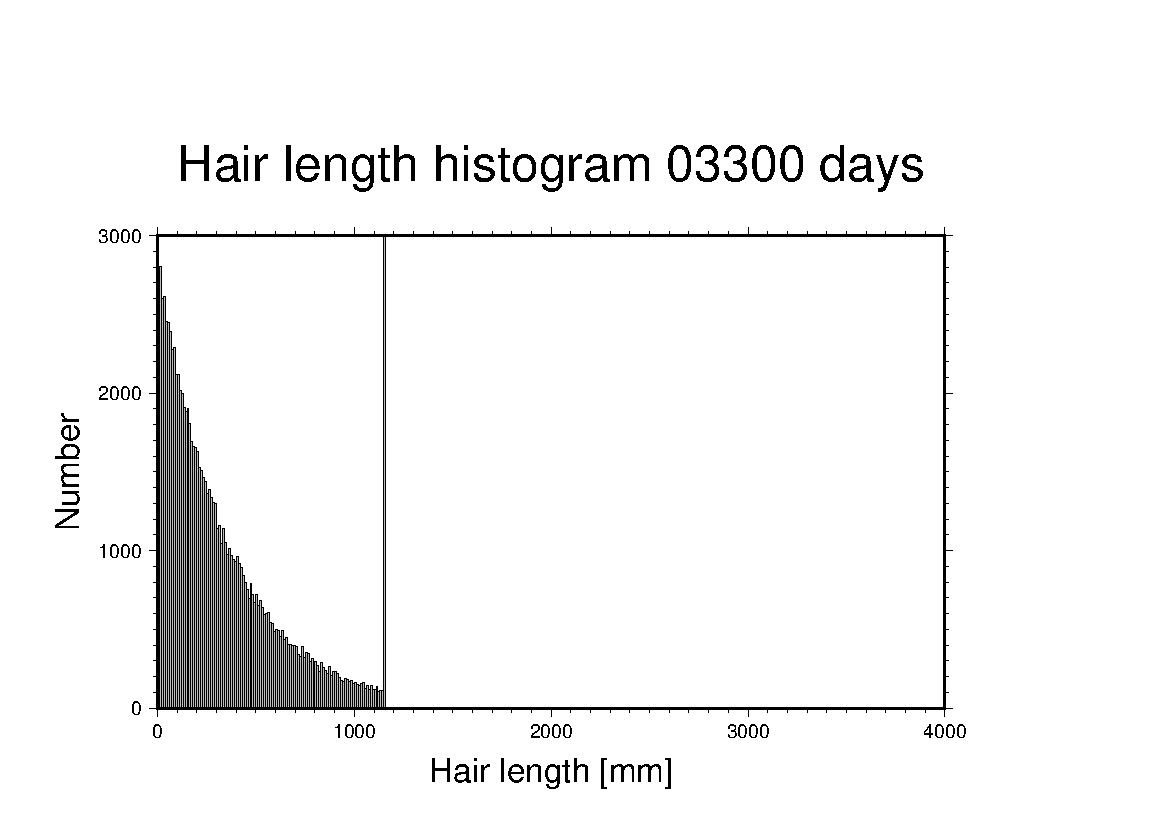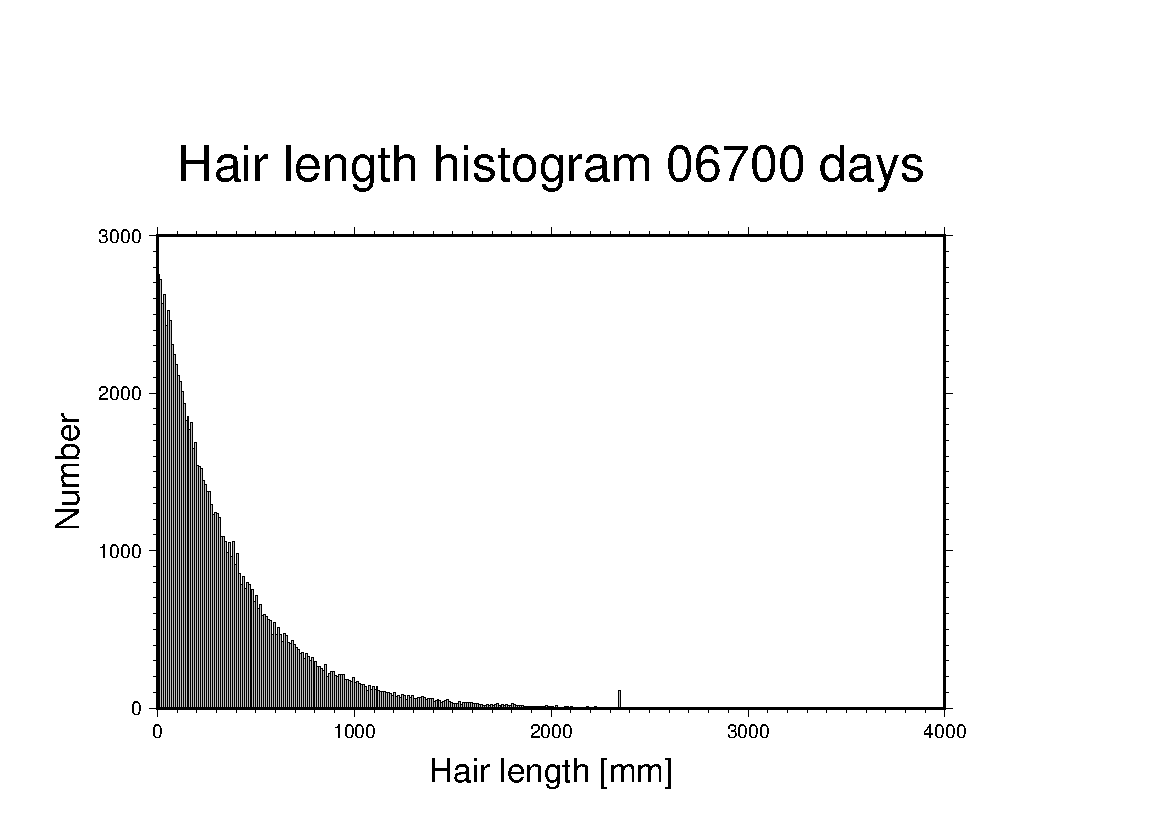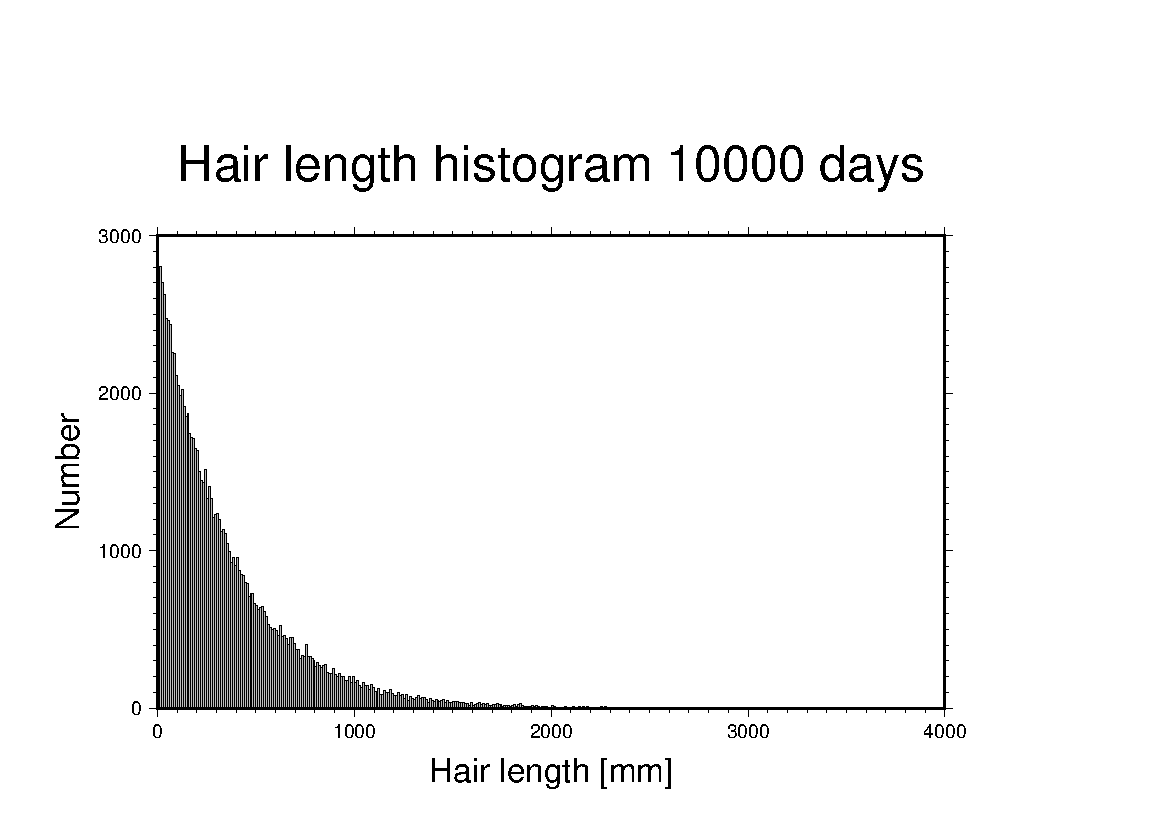目的
髪の毛は切らなければ伸び続けるというのは、常識である。しかし、髪の毛が一定確率で抜けるのであれば、髪の毛の平均の長さは限界があるのではないだろうか。本紙では、数値シミュレーションを用いて髪の毛の長さの時間経過をシミュレーションし、その特徴を調べる。
方法
髪の毛の本数は100000本1、ある髪が1日に髪の毛が抜ける確率を$\frac{1日に抜ける髪の本数}{髪の本数}$とし、1日に抜ける本数を100本2とした。また、髪の毛は抜けると同時に新しく生えるとし、髪全体の本数は不変であるとした。どの髪の毛も0.35 mm/day3で伸びるとする。髪がまったくない状態を初期条件にした。
結果
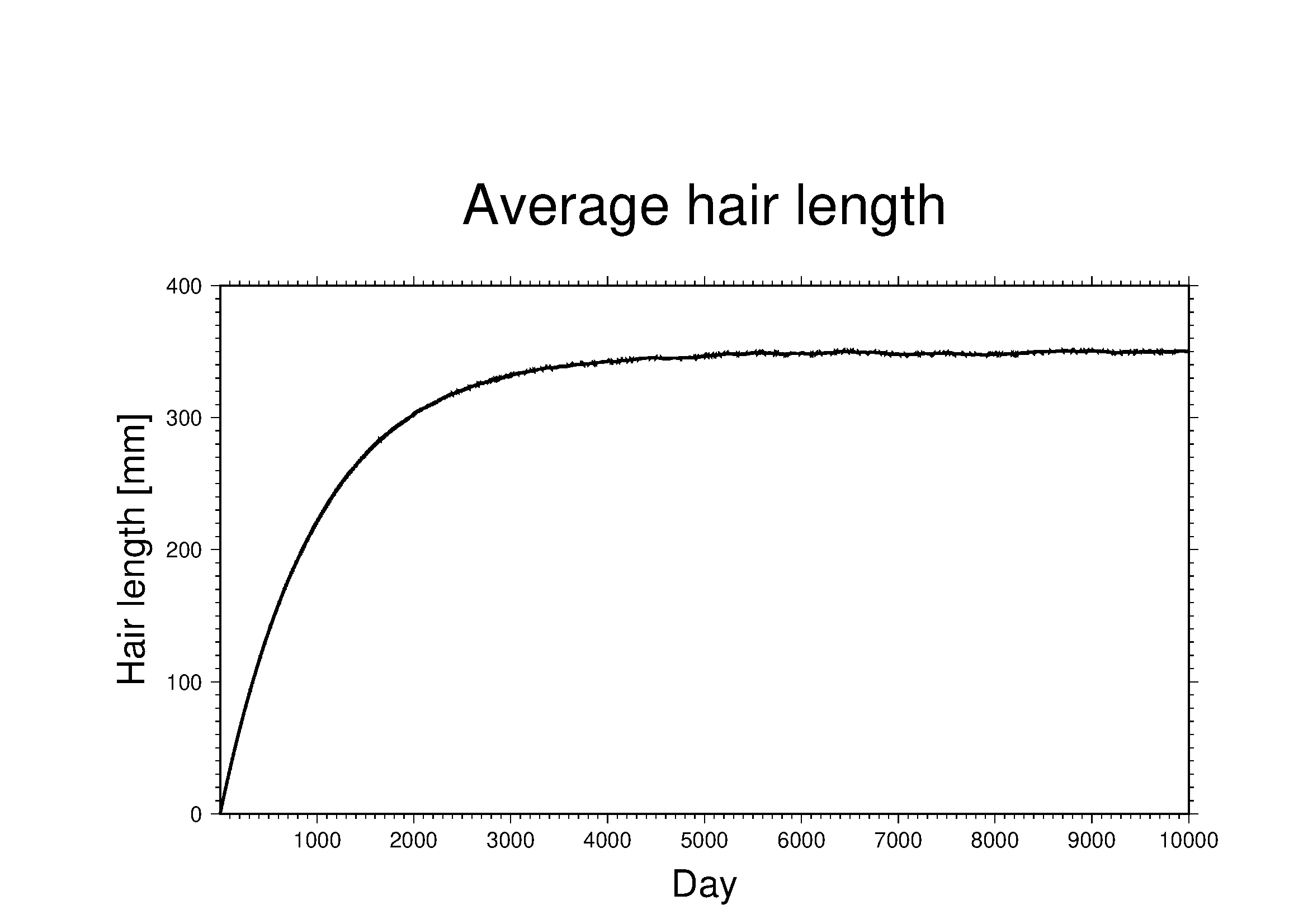
髪の毛の平均の長さは以下のようになった。
3000日前後から平均の髪の毛の長さが350 mmほどで安定してる。
髪の毛の長さのヒストグラムは以下のようになった。
多少の擾乱はあるが、指数分布に安定している。
考察
数値実験の結果から、髪の毛の平均の長さは無限に長くならないことが分かった。この結果を解析的に導けないか試してみる。
髪の毛の長さを$x$の本数を$h$とし、髪の毛の長さ分布の時間変化が成長と、抜けることによる影響しかないと仮定すると、
$$
h(x,t + \Delta t) \Delta x
= h(x,t) \Delta x
- h\left(x - \frac{\Delta x}{2}- g \Delta t , t \right) g \Delta t
- h\left(x + \frac{\Delta x}{2}- g \Delta t , t \right) g \Delta t
- p \Delta t \cdot h(x,t) \Delta x
$$
と書ける。ただし、$g$は髪の毛の成長速度、$p$は髪の毛の抜ける確率だとする。$\Delta x \to 0, \Delta t \to 0$とすると、
$$
\frac{h(x, t + \Delta t) - h(x,t)}{\Delta t} = - g \frac{ h\left(x + \frac{\Delta x}{2}- g \Delta t , t \right)
- h\left(x - \frac{\Delta x}{2}- g \Delta t , t \right) }{\Delta x} - p h(x,t) \
\frac{\partial h}{\partial t}
= - g \frac{\partial h}{\partial x} - ph
$$
と微分方程式を導くことができる。ちなみにこの偏微分方程式の解は任意関数$h_0(x)$を用いて
$$
h(x,t) = h_0(x-gt)e^{-pt}
$$
と書けるなんで。定常$\frac{\partial h}{\partial t}=0$を仮定すると、
$$
g \frac{\partial h}{\partial x} = -ph \
\frac{1}{h} dh = - \frac{p}{g} dx \
\int \frac{1}{h} dh = - \frac{p}{g} \int dx \
\ln h = - \frac{p}{g} x + C \
h = A \exp \bigg( - \frac{p}{g} x \bigg)
$$
$h$の正規性$\int_0^\infty h(x) dx = 1$を用いると、
$$
\int_0^\infty A \exp{\left( - \frac{p}{g} x \right)} dx \
= A \left[ - \frac{g}{p} \exp{ \left( - \frac{p}{g} x \right)} \right]_0^\infty \
= A \frac{g}{p} = 1 \
A = \frac{p}{g}
$$
したがって、十分時間がたった髪の毛の長さの分布は、
$$
h(x) = \frac{p}{g} \exp{\left( - \frac{p}{g} x \right)}
$$
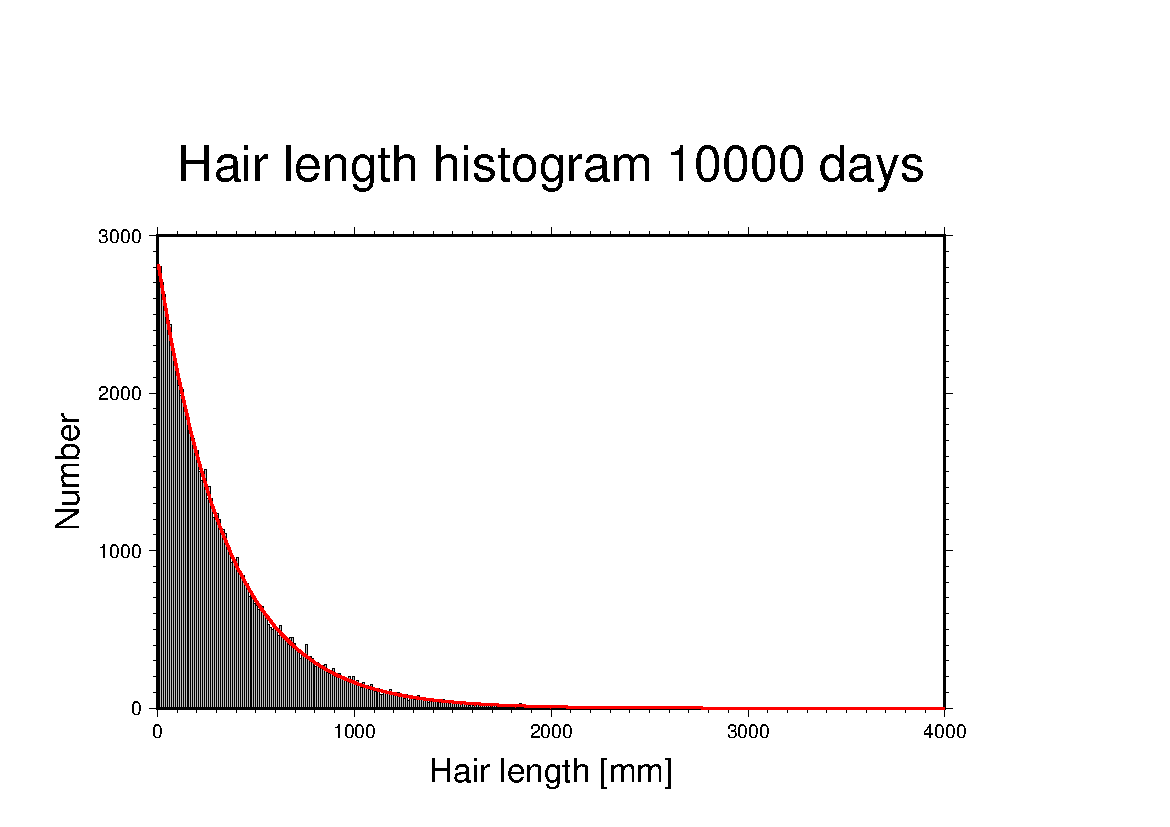
となる。ここで、$p = 10^{-3}$ [day^-1^]、$g = 0.35$ [mm day^-1^]を用いて、数値解に重ねると、
となった。したがって、定常解は
$$
g \frac{\partial h}{\partial x} = -ph
$$
という微分方程式に従うと言える。
付録
fortranのコードを付けておきます。スレッド並列化したので、多少早く実行できます。
program hair
!$ use omp_lib
implicit none
integer, parameter :: time_max = 100*100
integer, parameter :: hair_num = 100000
integer, parameter :: escape_num = 100 ! [/day]
integer, parameter :: output_step = 100
real(8), parameter :: speed_hair = 0.35 ! [mm/day]
real(8), dimension(1:hair_num) :: length_hair
real(8) :: prob_escape
real(8) :: random
real(8) :: total_length, total_length_2
real(8) :: time_start, time_end
integer :: escaped_hair
integer :: time_i, hair_i
! initialize
! prob_escape = dble( escape_num ) / dble( hair_num )
prob_escape = 1.d-3
length_hair(:) = 0.d0
print *, "-----------------------------------"
print *, " hair_num = ", hair_num
print *, " speed_hair = ", speed_hair
print *, " prob_escape = ", prob_escape
print *, "-----------------------------------"
call output( 0, hair_num, length_hair )
open(11, file='./output/stat.txt', status='replace')
!$ time_start = omp_get_wtime()
do time_i = 1, time_max
escaped_hair = 0
total_length = 0.d0
total_length_2 = 0.d0
!$OMP parallel do private(random) reduction(+:escaped_hair) reduction(+:total_length) reduction(+:total_length_2)
do hair_i = 1, hair_num
call random_number( random )
if ( random < prob_escape ) then
! escape hair
length_hair(hair_i) = 0.d0
escaped_hair = escaped_hair + 1
end if
length_hair(hair_i) = length_hair(hair_i) + speed_hair
total_length = total_length + length_hair(hair_i)
total_length_2 = total_length_2 + length_hair(hair_i)**2
end do
!$OMP end parallel do
if ( mod( time_i, output_step ) == 0 ) then
print *, time_i, total_length/dble(hair_num)
call output( time_i, hair_num, length_hair )
end if
write(11, '(I5.5, 3X, I3.3, 3X, 3(f15.5, 3X))') time_i, &
escaped_hair, &
total_length/dble(hair_num), &
total_length_2/dble(hair_num)-(total_length/dble(hair_num))**2, &
maxval(length_hair(:))
end do
!$ time_end = omp_get_wtime()
!$ print *, "time = ", time_end - time_start
close(11)
contains
subroutine output( time_i, hair_num, length_hair )
implicit none
integer, intent(in) :: time_i
integer, intent(in) :: hair_num
real(8), dimension(1:hair_num), intent(in) :: length_hair
integer :: hair_i
character(128) :: filename
write(filename, '("./output/length/length"I5.5".txt")') time_i
open(10, file=filename, status='replace' )
do hair_i = 1, hair_num
write(10,*) hair_i, length_hair(hair_i)
end do
close(10)
end subroutine output
end program hair