追記 (22th,Apr,2024)
参考文献のリンク先が切れていたため、修正。
追記(15th,May,2022)
修正点
GraphPadPrismの結果Hill係数の部分に、UpperとEstの結果を逆に示すという誤りがあったため修正した。
(それ以外にも3月にはMarkdownの数式の部分で指摘を受けたためこっそり修正している・・・・・・)
追記(30th,Nov,2022)
EC50の検定、効力比について追記した。
おことわり
本記事は数式を用いるが、数学的厳密性に関しては無視する点お断りしておく。
はじめに
研究室で$IC_{50}$を出すのにどうすれば良いのか後輩から聞かれた。その際GraphPadPrismを用いた算出法をを教えた。教えているときにRやExceldでPrismと同じような結果を出力する方法が気になったので、この記事にまとめておく(まあ純粋にPrismだけ使っておけば良いだろうという突っ込みはあるかもしれないが)
環境
GraphPadPrism: GraphpadPrism7
R:
> sessionInfo()
R version 4.1.1 (2021-08-10)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19042)
Excel
Office365Applications
用量反応曲線とは
まず用量反応関係とは、ある化学物質などの刺激を与えた際に培養細胞や実験動物などに投与したときに横軸を刺激の強さ(化学物質の量)、縦軸を反応を示す強さの形で得られる関係のことである。
この用量反応関係はシグモイド曲線(S字曲線)の形を取る。
シグモイド曲線を取る曲線として以下のものが上げられる。
-
シグモイド曲線を取る曲線
-
正弦曲線
-
ロジスティック曲線
-
プロビット曲線
-
そして今回はこの中でもロジスティク曲線を用いて用量反応曲線の推定する方法について主に概説する。
ロジスティック曲線
説明変数$x$と出現率$p$の関係がロジスティック曲線で表される曲線
\begin{align}
\mathop{\rm logit}\nolimits(p_k) &= \ln (\frac{p_k}{1-p_k})\\
&= \alpha + \Sigma (\beta_kx_{k,i})+\epsilon\\
p_k &= \frac{r_k}{n_k}\\
\\
p_k &\colon \, 出現率\\
\end{align}
Reed-Munchの方法
まずは最も簡便に求められると思われるReed-Munchの方法である。
この方法は、Responseが50(%)を超えた最も近い測定点とResponseが50(%)を超えない最も近い測定点の2点間の直線の傾きを求める。そしてこの直線を用いて、$IC_{50}$や$EC_{50}$や$LC_{50}$を求める。
\begin{align}
\frac{(\% pos.above \,50 \%)-50 \%}{(\% pos.above \, 50 \%)-(\% pos.below \, 50 \% )} &= proportionate\, distance\\
\\
\log (dilution\, above\, 50 \%) \, +\\
\, \, \, \,proportionate\, distance \times (dilution \, factor) &= IC_{50}\\
\\
dilution\, factor &= \log (dilution\, above\,50 \% )-log (dilution\, below\, 50 \%)\\
\end{align}
ただこの方法は用量反応関係を純粋に直線になるようにplotする方法であり、plotした0と100の部分が$IC_0$や$IC_{100}$でない可能性がある。そのため、次に説明する方法で求めることが多い。
ロジスティック曲線を用いた近似
今回Excel、GraphPadPrismで用いられている方法は非線形最小二乗法であり、GraphPadPrismではMarquardt法(Levenberg-Marquardt法とも)(調べたところによれば、極値から遠い場所では最急降下法を用い、極値に近くなった場合にはニュートン法を使うらしい・・・・・・)、ExcelのSolverでは一般化簡約勾配法(説明を読んだけれどどういうことか分からなかった・・・・・・(理解レベルは勾配法の一種なんだなと))を用いている。最適化の際に用いられるアルゴリズムに関する詳細な説明は専門書を読んで欲しい(てか僕に分かりやすく教えて欲しい)。
4パラメータモデルは以下の通りになる。
$$
pred[i] = bottom + \frac{Top-bottom}{1+10^{hill(EC_{50}-Conc[i])}}
$$
※$EC_{50}$、Concは常用対数をとった値である(以下同様)。
今回用いるデータは、ガルバッタ氏がこの記事
で用いているデータである。
個々のパラメータを出す前にまずは図示
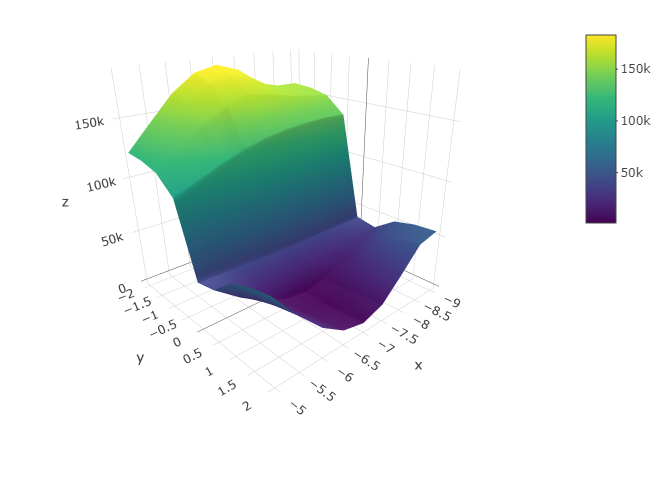
データがあったら、すぐ個々のパラメータを出したくなるのが人情なのだが、まずは一旦グラフを書いてみる。
この下のグラフはX軸がEC50、Y軸がHill係数、Z軸が残差平方和である。
このグラフから、だいたいコントロールの$EC_{50}$が-7近傍、処理群では-6近傍、双方ともHill係数が1近傍で残差平方和が最も小さくなるということが読み取れる。
GraphPadPrism
使い方を詳細に記載すると後々面倒なことになりそうなので、マニュアルにその説明を譲る。
Rでの計算
まずRで計算する。今回計算するにあたり、以下の条件を仮定して計算する。
・コントロール群と処理群ではHill係数、Baseが同じ。
この条件を仮定に従って計算するために、以下の数式で計算する。
$$
y_i= \frac{100}{1+10^{hill(Control群のEC_{50}\times \beta_1-Conc+処理群のEC_{50}\times \beta_2 )}}
$$
$\beta_1$はControl群であることを満たした時のカテゴリー変数、$\beta_2$は処理群であることを満たしたカテゴリー変数、$y_i$はResponse、$Conc$は濃度を示す。
数式はExcelで計算したときとおなじである。
library(tidyverse)
library(minpack.lm) #Marquardt(Levenberg-Marquardt法)を実行するためのパッケージ
conc<-dat_all2$Conc
Obs<-dat_all2$Response
Group<-as.integer(dat_all2$Group)-1
Group2<-as.integer(dat_all2$Group_2)
pred<-function(parS,xx,group,group2){
100/(1+10^(parS$b*(parS$c*group-xx+parS$t*group2)))
}
resid<-function(p,observed,xx,group,group2){
observed-pred(p,xx,group,group2)
}
parStart<-list(b=0.1,t=1,c=1)
nls.out<- nls.lm(par=parStart, fn=resid, observed=Obs,xx=conc,group=Group2,group2=Group,control=nls.lm.control(maxiter=1024,nprint=1))
上記を実行すると、
## It. 0, RSS = 150844, Par. = 0.1 1 1
## It. 1, RSS = 61152.5, Par. = 0.0651435 -8.10953 -10.4787
## It. 2, RSS = 49101, Par. = 0.100639 -6.87531 -8.23275
## It. 3, RSS = 30665.2, Par. = 0.188781 -6.16607 -6.95798
## It. 4, RSS = 11215.3, Par. = 0.372797 -6.12048 -7.04331
## It. 5, RSS = 3111.78, Par. = 0.65959 -5.99114 -6.79121
## It. 6, RSS = 2072.54, Par. = 0.801159 -6.07132 -6.91557
## It. 7, RSS = 2056.11, Par. = 0.830435 -6.06712 -6.91184
## It. 8, RSS = 2056.04, Par. = 0.829753 -6.0683 -6.91331
## It. 9, RSS = 2056.04, Par. = 0.829894 -6.06825 -6.91331
## It. 10, RSS = 2056.04, Par. = 0.829888 -6.06826 -6.91332
となることが読み取れる。
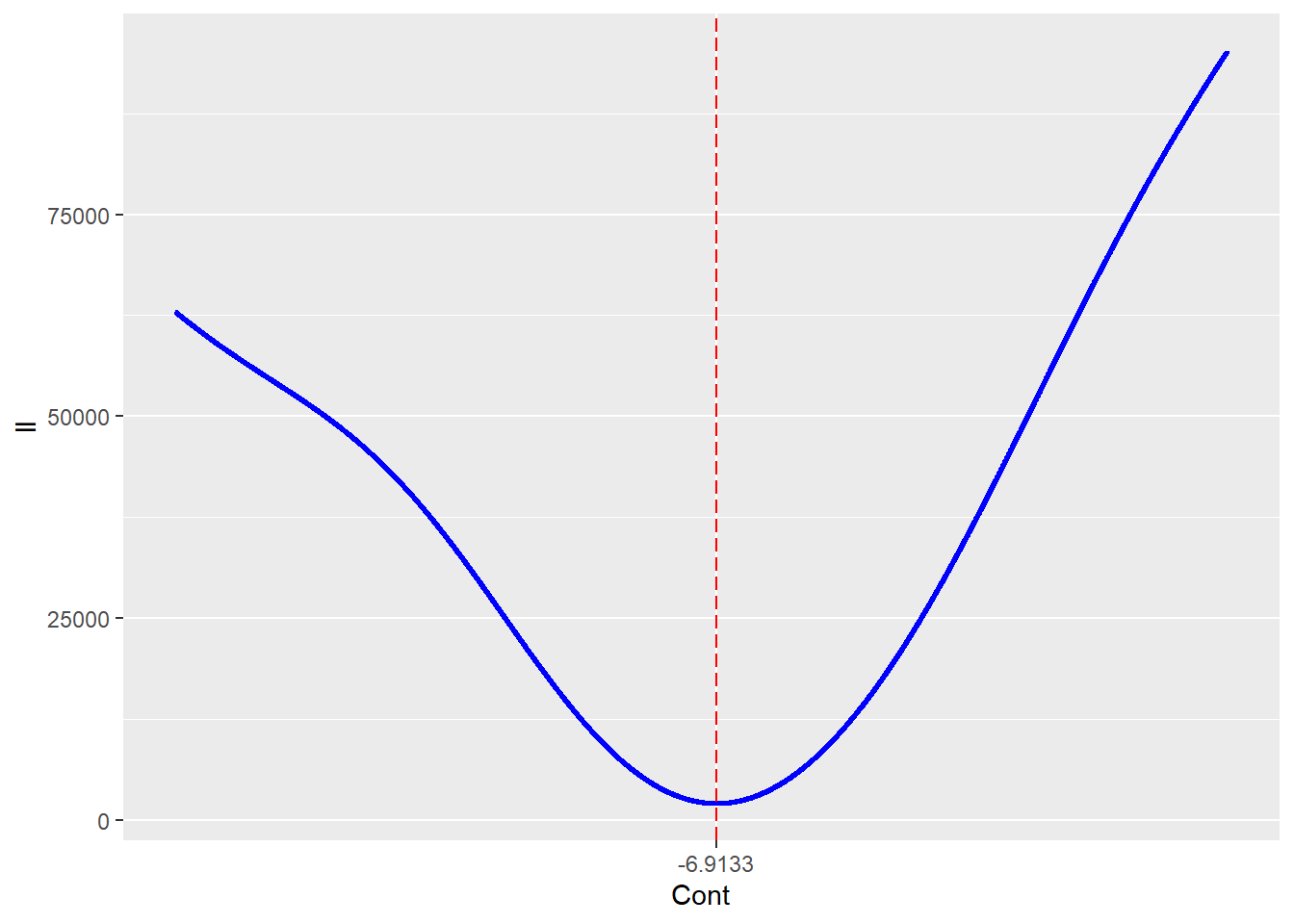
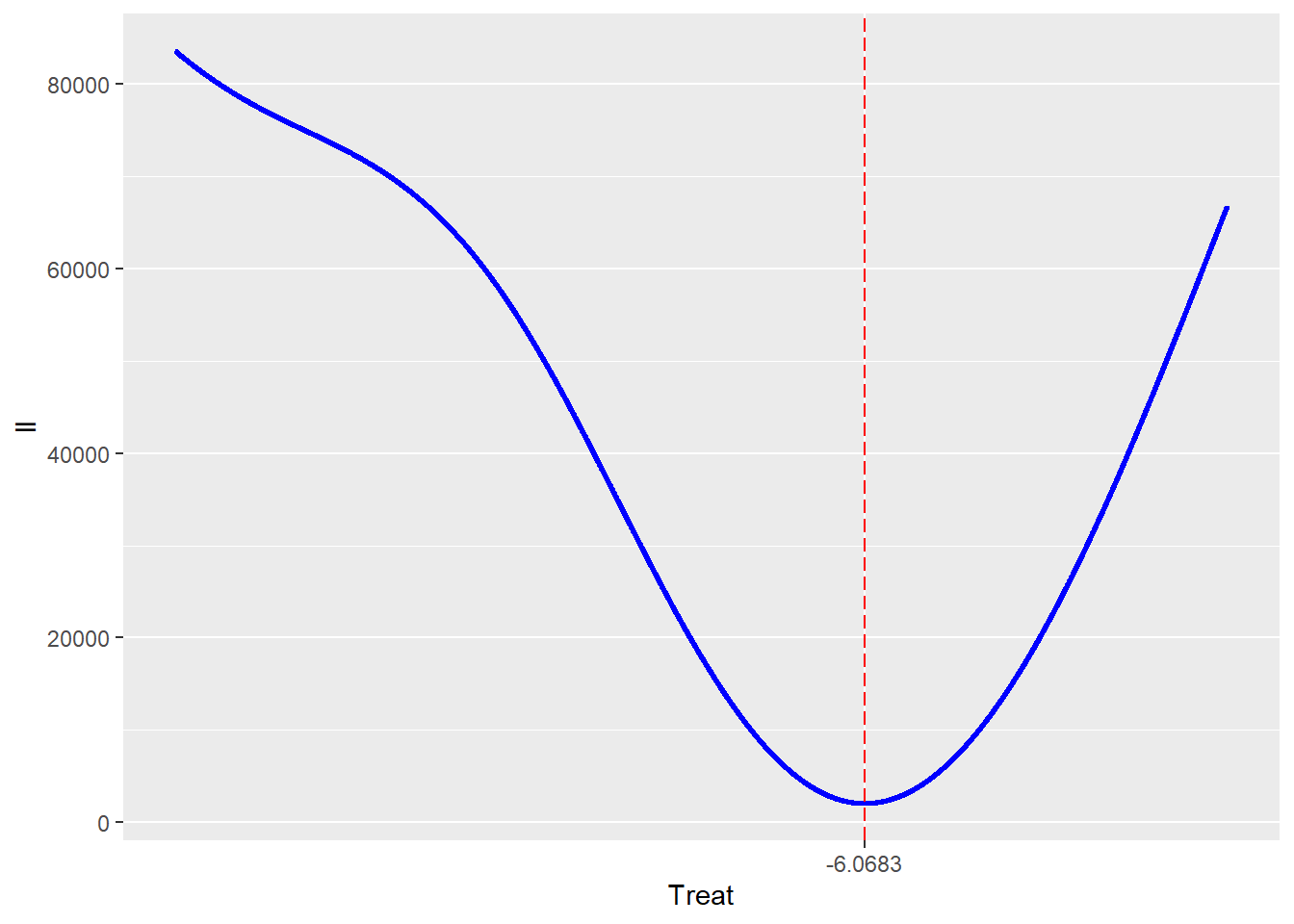
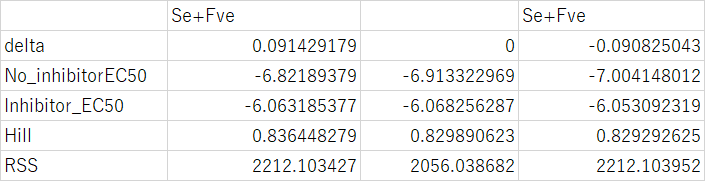
ここで、推定したHill係数-RSS、Control群の$EC_{50}$-RSS、処理群の$EC_{50}$-RSSの関係についてプロットは以下のようになる。
推定したHill係数-RSS
Control群の$EC_{50}$-RSS
処理群の$EC_{50}$-RSS
いずれのパラメータを見てもらえばわかるように残差平方和が極小値となる点を見たとき、残差平方和の関数が左右対称を示さないことが分かる。
ここでProfile-Likelyhoodという考え方を用いて、各パラメータの95%信頼区間を求める。
Profile-Likelyhood
流れとしては
、
95%信頼区間を推定したいパラメータ以外は推定値で固定し、残差平方和を求める
↓
上記で求めた残差平方和を、最も小さくなるときの残差平方和と自由度1のときの95 (%)確率をとるF分布の確率点で引く
↓
このときの値が0となる値が95%信頼区間の値なので、その値をuniroot関数で求める
という処理になる。
※尤度関数が上に凸の値を取る場合はF分布でなく$\chi^2$分布を用いる。
この推定をRで行うにあたっては以下のサイトを参考にした。
#最小の残差平方和と各パラメータを取り出す
r.out<-nls.out$deviance
c<-nls.out$par$c
b<-nls.out$par$b
t<-nls.out$par$t
#データのサンプルサイズを取り出す
n_all2<-nrow(dat_all2)
#自由度を計算する。
df<-n_all2-3
qlevel<-qf(0.95,1,df)
#Control群のProfile Likelyhodd
#誤差関数から残差平方和の最小値と、並びに自由度1のときの95 (%)確率をとる
#F分布の確率点に自由度で割った残差平方和の最小値を掛け合わせた値を引く処理を行った関数を定義する
residB<-function(cont,qlevel){
f<-sum((Obs-100/(1+10^(b*(cont*Group2-conc+t*Group))))^2)
f2<-f-r.out-qlevel*r.out/df
return(f2)
}
#Uniroot関数で上記の関数が0になるときの値を求める
Cont_lower<-uniroot(residB,interval = c(-10,nls.out$par$c),qlevel)$root
Cont_upper<-uniroot(residB,interval = c(nls.out$par$c,-4),qlevel)$root
#Treat群のProfile Likelyhodd
residC<-function(treat,qlevel){
f<-sum((Obs-100/(1+10^(b*(c*Group2-conc+treat*Group))))^2)
f2<-f-r.out-qlevel*r.out/df
return(f2)
}
Treat_lower<-uniroot(residC,interval = c(-10,nls.out$par$t),qlevel)$root
Treat_upper<-uniroot(residC,interval = c(nls.out$par$t,-4),qlevel)$root
#Hill係数のProfile Likelyhodd
residD<-function(hill,qlevel){
f<-sum((Obs-100/(1+10^(hill*(c*Group2-conc+t*Group))))^2)
f2<-f-r.out-qlevel*r.out/df
return(f2)
}
hill_lower<-uniroot(residD,interval = c(0,nls.out$par$b),qlevel)$root
hill_upper<-uniroot(residD,interval = c(nls.out$par$b,2),qlevel)$root
EC50_Cont_est<-nls.out$par$c
EC50_Treat_est<-nls.out$par$t
hill_est<-nls.out$par$b
EC50_est<-matrix(NA,nrow=3,ncol=2)
Hill_est<-matrix(NA,nrow=3,ncol=2)
EC50_est[1,]<-c(Cont_upper,Treat_upper)
EC50_est[2,]<-c(EC50_Cont_est,EC50_Treat_est)
EC50_est[3,]<-c(Cont_lower,Treat_lower)
Hill_est[1,]<-c(hill_lower,hill_lower)
Hill_est[2,]<-c(hill_est,hill_est)
Hill_est[3,]<-c(hill_upper,hill_upper)
rownames(EC50_est)<-c("EC50_upper","EC50","EC50_lower")
colnames(EC50_est)<-c("Cont","Treat")
rownames(Hill_est)<-c("Hill_upper","Hill","Hill_lower")
colnames(Hill_est)<-c("Cont","Treat")
EC50_est
Hill_est
上記のコードを実行すると、
EC50_est
## Cont Treat
## EC50_upper -6.821154 -5.978542
## EC50 -6.913318 -6.068257
## EC50_lower -7.005459 -6.157889
Hill_est
## Cont Treat
## Hill_upper 0.7445447 0.7445447
## Hill 0.8298877 0.8298877
## Hill_lower 0.9286807 0.9286807
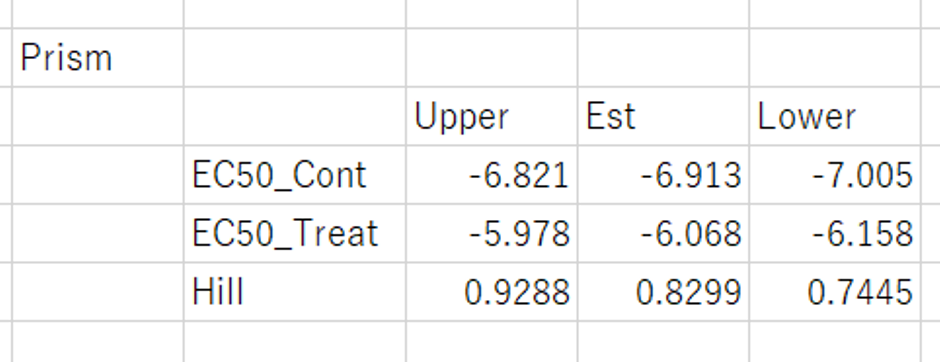
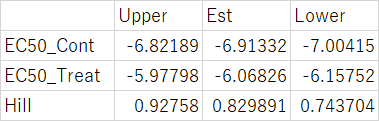
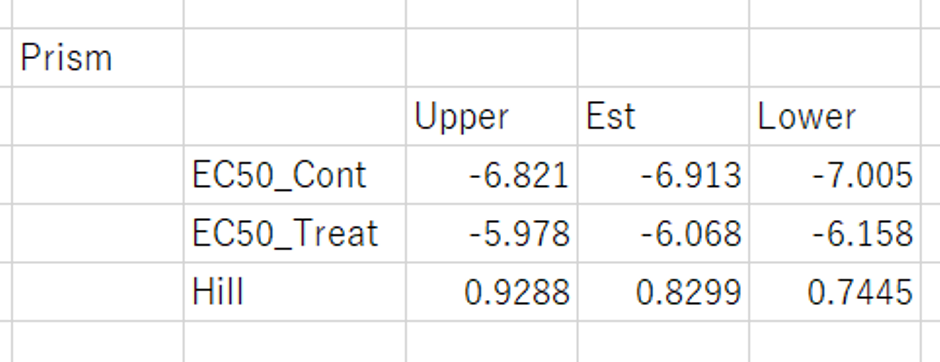
Prismの結果は下記のようになる
今回の場合、仮説検定で用いる近似信頼区間の値とProfile Likelyhoodでの信頼区間の値が対応しないことに注意すること。
出典:
第2期 医薬安全性研究会
非線形最小2乗法の基礎
(1) 線形モデルと非線形モデルの基本的な考え方
逆推定の解析,標準誤差と信頼限界 大和田 章一
https://biostat.jp/archive_teireikai_2_download.php?id=19
標準誤差を用いた95(%)信頼区間(R)
標準誤差を用いた95 (%)信頼区間は以下の流れで求める。
パラメータを推定する
↓
(もしSEが出ていなければ、推定したパラメータを目的変数として入力したときの勾配関数を求める)
↓
(求めた勾配関数と「勾配関数の転置行列」を掛け、その逆行列を出す)
↓
(パラメータ推定したときの残差平方和の最小値と上記の行列を掛けてそれを自由度で割る)
↓
パラメータを推定出来る。
(※誤差が正規分布に従うと仮定している)
この推定を行うにあたってはRのコードは以下のサイトを
数学的な裏付けについては
の重回帰モデルの分散を線型モデルで解いている部分を参考にした。
具体的な数式では
まず、Response $y_j$と用量反応曲線の関数$f(x_j,\beta)(x_j:Concentration,\beta:parameter)$
の誤差$\epsilon_j$は
$$
\epsilon_j=y_j-f(x_j,\beta)\
$$
の関係式で表すことが出来る。
そして、非線形回帰モデルでは分散共分散行列を
$$
f(x_j,\beta)\simeq f(x_j,\hat \beta)+\nabla f(x_j,\hat \beta)(\beta-\hat \beta) \
$$
$\epsilon:誤差$、$\nabla:f(x_j,\beta)の勾配$
で計算している。
ここで、
$$
g_j=\nabla f(x_j,\hat \beta)
$$
$$
z_j=y_j-f(x_j,\hat \beta)+\nabla f(x_j,\hat \beta)\hat \beta \space
$$
とおき、一番上の$\epsilon$の式に$x_j$の式を代入すると
z_j=g_j \beta+\epsilon_j\\
と変形できる。
そして、これをまとめると
$$
z=G\beta+ \epsilon (行列Gのg_j行目)
$$
と表すことが出来る。
そして証明は省略するがパラメータの推定値$\tilde{\beta}$は
\begin{align}
\tilde{\beta}&=\mathop{\rm arg}\mathop{\rm min}_{\beta}||z-G\beta||^2\\
&=(G′G)^{−1}G′z \\
&=(G′G)^{−1}G′(y-f(x,\hat \beta)+\nabla f(x,\hat \beta)\hat \beta) \\
&=\hat\beta+(G′G)^{-1}\nabla f(x,\hat \beta)(y−f(x,\hat\beta))
\end{align}
であり、分散共分散行列は
$$
\hat\beta=(G′G)^{−1}G′z
$$
より
$$
Var_{lin}(\beta)=\hat \sigma^2 (G′G)^{-1}
$$
(恐らくここら辺の行列表現は永田・棟近がわかりやすいと思う。)
今回はこれを実装する。
コードは以下のようになる
SEを出力してくれる場合
nls.out2<-summary(nls.out)[[8]]
SE<-nls.out2[,2]
#推定値とSEに95%確率点時のt統計量を足す
Upper<-nls.out2[,1]+SE*qt(0.975,df)
Lower<-nls.out2[,1]-SE*qt(0.975,df)
Est_1<-matrix(NA,nrow=3,ncol=3)
Est_1[1,]<-Upper
Est_1[2,]<-nls.out2[,1]
Est_1[3,]<-Lower
rownames(Est_1)<-c("Upper","Est","Lower")
colnames(Est_1)<-c("Hill","Treat","Cont")
Est_1
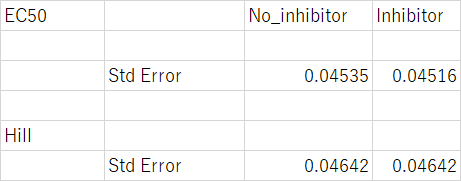
出力結果
Hill Treat Cont
Upper 0.9229941 -5.977683 -6.822358
Est 0.8298877 -6.068257 -6.913318
Lower 0.7367812 -6.158832 -7.004278
> SE
Hill Treat Cont
0.04641987 0.04515738 0.04534971
出力してない場合
#まず勾配関数を定義する
hx2<-deriv(y~100/(1+10^(hill*(Cont*group2-x+(group1)*Treat))),c("hill","Cont","Treat"),function(x,y,group2,group1,hill,Cont,Treat){}
)
conc<-dat_all2$Conc
Obs<-dat_all2$Response
Group<-as.integer(dat_all2$Group)-1
Group2<-as.integer(dat_all2$Group_2)
#勾配関数の値を求める
fr2<-hx2(conc,Obs,Group2,Group,nls.out$par$b,nls.out$par$c,nls.out$par$t)
#勾配関数の値を抽出する
G<-attr(fr2,"gradient")
#分散を求める
V.lin<-nls.out$deviance/(nrow(dat_all2)-length(nls.out$par))*solve(t(G)%*%G)
#上記の分散の平方根を求める(標準誤差)
se.lin<-sqrt(diag(V.lin))
>se.lin
hill Cont Treat
0.04641940 0.04534992 0.04515757
Graphpad Prismでの結果は下記の通りである。
Excelでの計算
次に、Excelで計算する。流れとしてはRで行った計算方法と同じである。Rと同じようにProfile Likelyhoodと標準誤差を用いる方法の二つの求め方について説明する。
その前にまず、各パラメータを推定する。
流れとしては以下のようになる。
$$
y_i= \frac{100}{1+10^{hill(EC_{50_{cont}}\times \beta_1-Conc+EC_{50_{treat}}\times \beta_2 )}}
$$
の数式をセルに打ち込み、それぞれの残差と残差の二乗を計算する。
↓
各残差の二乗を足し合わせて、残差平方和を求める。
↓
各パラメータの制約条件を入力して、残差平方和が最も小さくなる値をソルバー(GRG非線形)で求める。
具体的な手順を説明する。
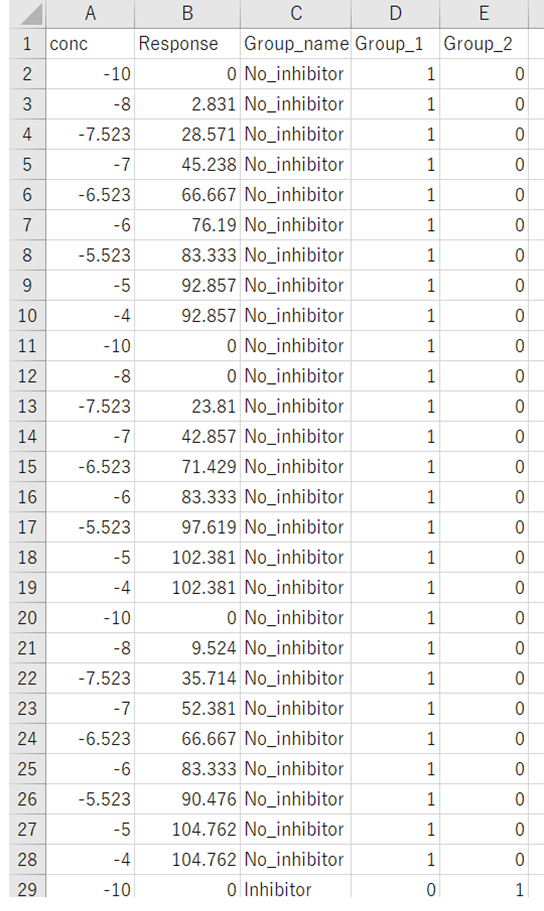
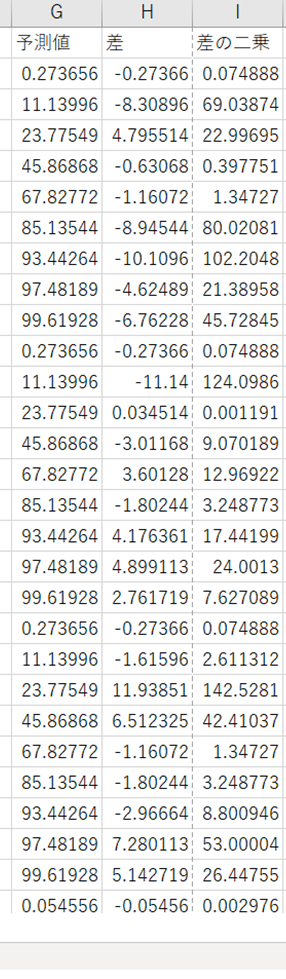
まずA列に濃度、B列にはResponce、C列に各Group名、D列、E列は各Groupをカテゴリー変数化したものを入力する。
そして、
G列のセルに
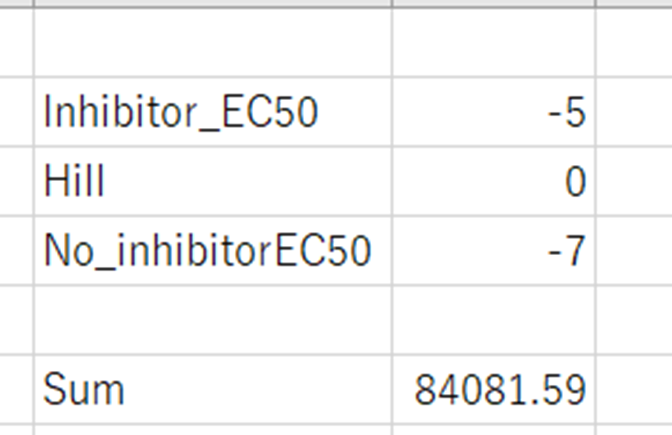
A、B、D、E列の変数と推定したいパラメータ(ここではInhibitorのパラメータをL2、Hill係数のパラメータをL3、No inhibitor(Control)のパラメータをL4)をセル参照を用いて入力する。
このとき、パラメータの値は適当(といっても取り得ると考えられる範囲の中で)に入力する。
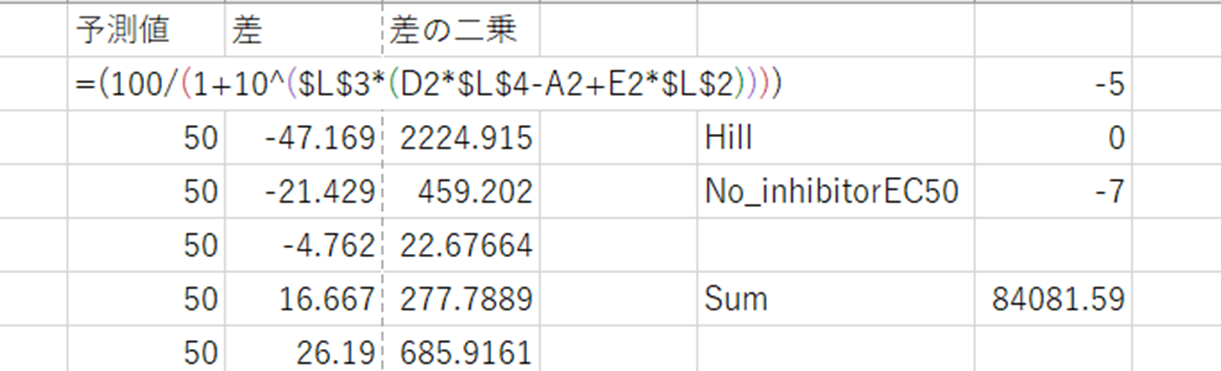
そしてG列で計算した値とB列(Response)との差をH列(差)に入力し、I列ではH列を二乗したものを入れる。
そして、残差平方和を計算したものをH6に入力し、この残差平方和が最小になるように計算を行う。
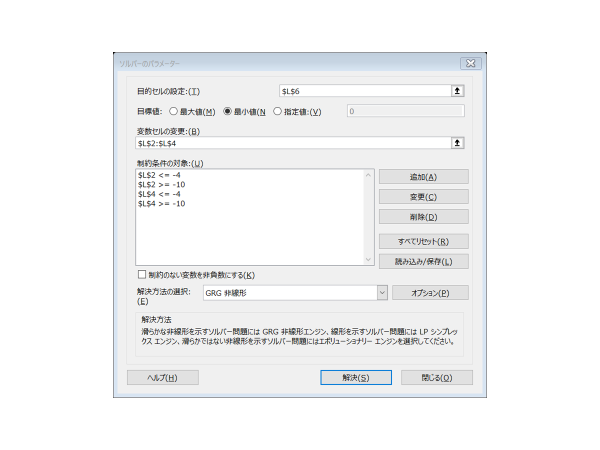
そしてソルバーを起動して、目的セルを残差平方和を求めたH6に、変数セルを各パラメータを入力したセルに設定する。
次に目標値を最小値に設定した後に、制約条件を入力する。今回の場合は、Control、Inhibitorともに、-10から-4の値の間に収まると考えられるので、これを制約条件に設定する。
そして、解決方法をGRG非線形に設定し解決をクリックする。
収束すると
というダイアログが出てくる。
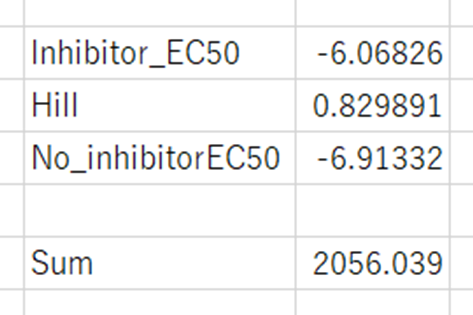
これで求まった値は、
となる。
Profile Likelyhood
ここの部分は芳賀先生の資料を元にしている。
まずNo inhibitor(Control)を求める。
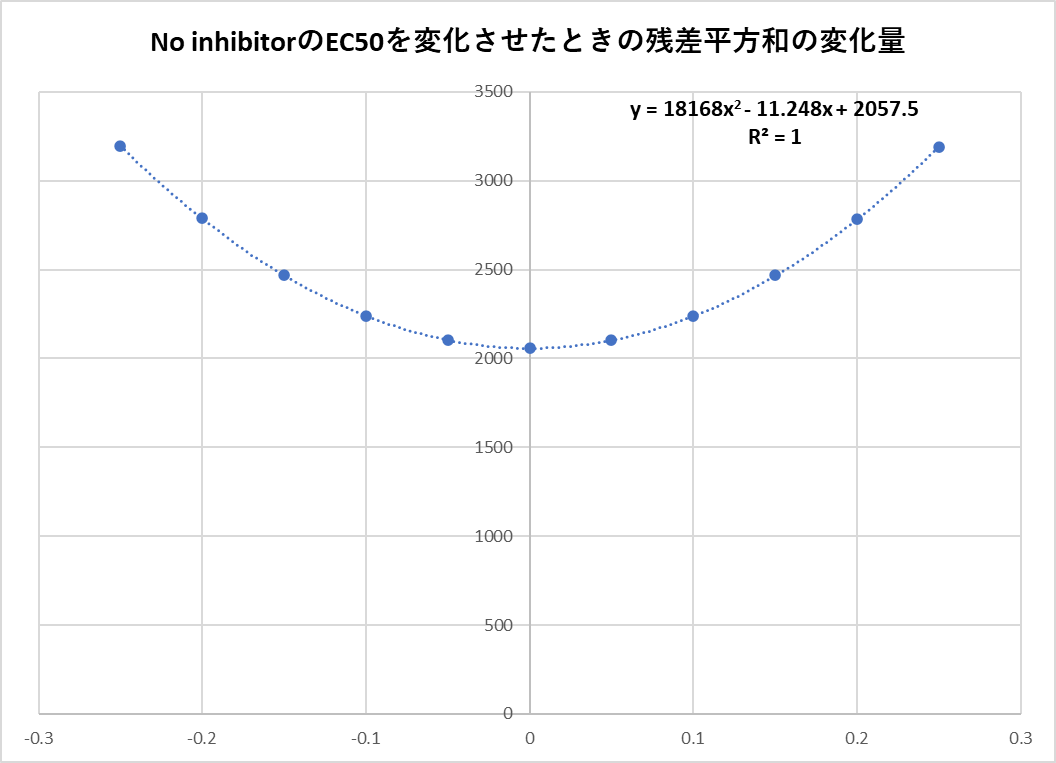
推定値からの誤差を$\delta$として、Controlの$EC_{50}$を$\delta$分だけ変化させたときの他のパラメータと残差平方和をソルバーで求める。
求めると下記のような値になるので、それを$x$軸を$\delta$、y軸をRSSとなるようグラフにする。
そして、グラフの設定から上記の点にうまくフィッティングするような多項式に近似させる。
今回は二次式を用いる。
多項式近似させた係数を下記の数式
$$
RSS=a\delta^2+b\delta+c
$$
のようにQに打ち込む。
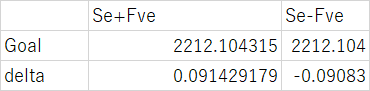
そしてGoalの部分には
$$
Goal=RSS+\frac{RSS}{df}(自由度1、自由度53、95\%区間)F分布の確率点
$$
と打ち込む。
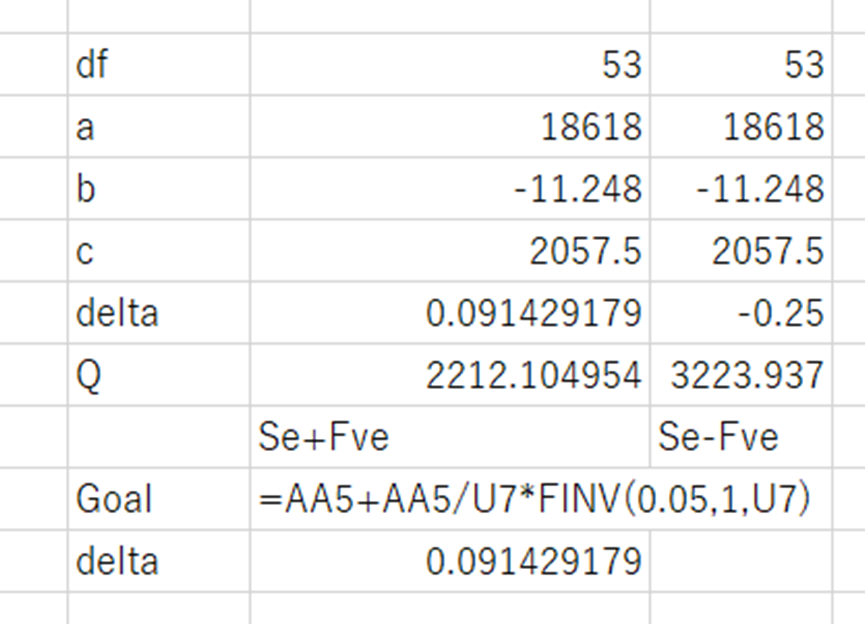
このGoalになるときの$\delta$をゴールシークで探索する。
このときゴールシークの解は2つもつことになるから、正負の$\delta$それぞれゴールシークを用いて推定する必要がある。
数式入力セルにはQの部分を、目標値は直接Goalの値を打ち込み、変化させるセルを$\delta$の部分を設定して、OKを押す。
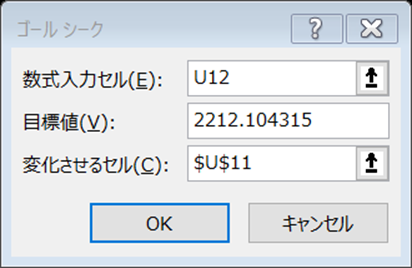
そして、$Control$の$EC_{50}$に$\delta$を足したときのRSSが2212.103427になるときの他のパラメータの値をソルバーで求める。
以下同様の作業を行う。
もう一度出すが、Prismの結果は下記のようになる
標準誤差
Rの場合と異なりExcelには勾配関数を算出する関数がないため、自分でセルに数式を入れて勾配関数を求める必要がある。
今回勾配関数を求める式は中心差分法を用いて計算した。以下のようになる
$$
Hill=\frac{\frac{100}{1+10^{((hill+1/2h)(Cont\times EC_{50_{Cont}}-Conc+Group\times EC_{50_{Treat}})}}-\frac{100}{1+10^{(hill-1/2h)(Cont\times EC_{50_{Cont}}-Conc+Group\times EC_{50_{Treat}})}}}{h}
$$
$EC_{50_{Cont}}$や$EC_{50_{Treat}}$も同様にして入力する。。
そして、$h$の幅を$10^{-6}$と入力して、すべての説明変数について計算する。
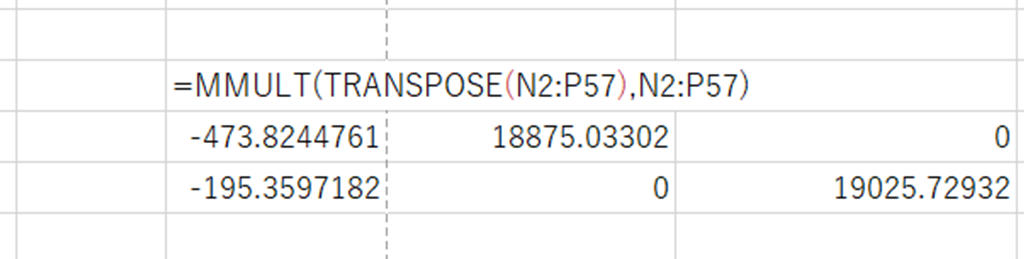
そして、MMULT関数を用い行列を用いて、各勾配を転置させた行列と転置させていない行列の積を求める。
この行列が共分散行列になる。
このそしてこの対角成分に残差平方和を掛けて、自由度で割れば各々のパラメータの分散が求まる。
この分散の平方根を取れば標準誤差が求まる。
Hill係数がNo inhibitorとInhibitorで別々の値を取るとき
この場合は、上記までの計算方法と違ってNon inhibitorとInhibitorのGroupをカテゴリー変数にする必要がない。そのため数式は、
$$
y_i = bottom\ + \frac{Top-bottom}{1+10^{hill(EC_{50}-Conc)}}
$$
を各グループに当てはめて計算すれば良い。
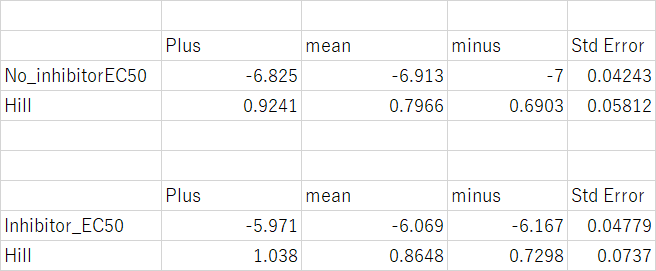
方法は同じなので結果だけ示す。
Prism
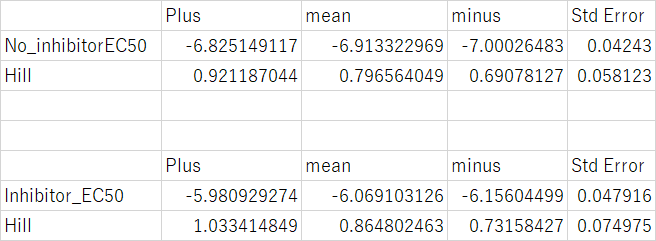
R
> EC50_est_2
Cont Treat
EC50_upper -6.825090 -5.970969
EC50 -6.912636 -6.069103
EC50_lower -7.000197 -6.167121
> Hill_est_2
Cont Treat
Hill_upper 0.6902746 0.7298525
Hill 0.7965701 0.8648019
Hill_lower 0.9240182 1.0375800
> se.lin_a
hill EC
0.05812364 0.04243048
> se.lin_b
hill EC
0.07369828 0.04778634
Excel
EC50の検定(追記:30th,Nov,2022)
Non inhibitorとInhibitorの$EC_{50}$がそれぞれ異なっていることを述べるためには、2群が共通した$EC_{50}$を持つという非線形モデルを帰無仮説とする。
$$
y_{pred}=\frac{100}{1+10^{hill\times(EC_{50_{\ common}}-Conc)}}
$$
F検定を用いたモデルの比較は以下の手順に従っている(根本的には尤度比検定である)。
まず。帰無仮説時のmodelの最小二乗和を求める。
そしてもし帰無仮説が等しければ、増分平方和(SS)と増分自由度(df)の関係が
$$
\frac{SS_{null}-SS_{compare}}{SS_{compare}}=\frac{df_{null}-df_{compare}}{df_{compare}}
$$
の関係が等しいことを仮定され、もし帰無仮説が棄却されるときは
$$
\frac{SS_{null}-SS_{compare}}{SS_{compare}}\geq \frac{df_{null}-df_{compare}}{df_{compare}}
$$
の関係となる。
そこで右辺を左に移行し、F検定を行う。
$$
\frac{SS_{null}-SS_{compare}}{SS_{compare}}\times \frac{df_{compare}}{df_{null}-df_{compare}}\geq F(df_{null}-df_{compare},df_{compare})
$$
>F
[1] 166.2024
> p_val<-1-pf(F,df_all-df,df)
> p_val
[1] 0
となり帰無仮説が棄却されるため、No inhibitor、Inhibitor間の$EC_{50}$は同じとは言えない。
ちなみにHill係数を分けて推定するモデルとHill係数が共通しているモデルを比較した場合、
> F_each
[1] 0.08503945
> p_each
[1] 0.771741
となり、Hill係数が2群で共通のモデルを採択する。
同じことはAICcの比較でも述べることができる。
その前にAICは、
$$
AIC = −2 ln(L)+2k
$$
L:最尤法で推定したモデルの尤度)
k:モデルの自由パラメータ数
で表され、
有限修正されたAICの場合は、
$$
cAIC = −2 ln(L)+\frac{2n\times k}{n-k-1}
$$
で表される。
個々のc-AIC(AICc)の差を取ると
\begin{align}
\delta(cAIC) &= −2 ln(L_A)+\frac{2n\times k_A}{n-k_A-1}-(−2 ln(L_B)+\frac{2n\times k_B}{n-k_B-1}) \\
&=2ln(\frac{L_B}{L_A})+2n\frac{k_A(n-k_B-1)-k_B(n-k_A-1)}{(n-k_A-1)(n-k_B-1)}\\
&=2ln(\frac{L_B}{L_A})+2n\frac{(n-1)(k_A-k_B)}{(n-k_A-1)(n-k_B-1)}
\end{align}
となり、この値が負の値をとれば比較したモデルBがよく当てはまり、正の値ではモデルAが良く当てはまる。
そして最小二乗法を用いた場合のc-AIC(AICc)は
$$
\delta(cAIC)=nln(\frac{RSS_{compare}}{RSS_{null}})+2n\frac{(n-1)(k_A-k_B)}{(n-k_A-1)(n-k_B-1)}
$$
RSS:残差平方和
となる。
これを計算すると
#2群でヒル係数とEC50が共通しているモデルとEC50だけが異なっているモデルとの比較
>del_AIC_c
[1] -77.35105
#2群でヒル係数とEC50それぞれ存在するモデルととEC50だけが異なっている場合との比較
> del_AIC_c_each
[1] 2.143617
となり、Hill係数が2群で共通のモデルの方が当てはまりが良いモデルである。
効力比(追記:30th,Nov,2022)
効力比については、以下の説明が詳しい。
端的に述べると、効力比とは、2つの薬剤を同じ用量用いた時の薬効(薬理作用)の比のことである
効力比が1を超えると対照群と比べて薬効発揮のために多い用量を投与する必要があり、1未満であればより少ない用量で薬効を発揮する。
$$
pred_i= \frac{100}{1+10^{hill(Control群のEC_{50}\times \beta_1-\frac{Control群のEC_{50}}{Ratio} \space \times \beta_2 )}}
$$
$\beta_1$、$\beta_2$:カテゴリー変数。
の式で直接推定することが出来る。
これを推定すると、
> EC50_est
EC50
EC50_upper -7.103588
EC50 -7.017800
EC50_lower -6.931953
> Hill_est
Hill
Hill_upper 0.6804584
Hill 0.7811531
Hill_lower 0.9022545
>Ratio_est_matrix
[,1]
Ratio_upper 1.159240
Ratio 1.180929
Ratio_lower 1.203485
#注Profile-likelyhoodを用いて推定
効力比の信頼区間が1をまたがないため、Treat群はControl群と比べて薬効発揮しているといえる。
最後に
まあ正直な話こんなややこしいことをしなくても、ソフトウェアを使って解けば良いんじゃないのかと思う(これまでの努力は)。
参考文献
ガルバッタ氏のブログ
用量反応曲線のEC50の標準偏差を出す
Nonlinear regression
http://sia.webpopix.org/nonlinearRegression.html
(22th,Apr,2022:追記 リンク先に飛ぶと詐欺サイトに飛ぶ可能性が出たため、以下のアーカイブに)
多変量解析法入門
永田 靖、棟近雅彦
https://www.saiensu.co.jp/search/?isbn=978-4-7819-0980-6&y=2001
第2期 医薬安全性研究会
非線形最小2乗法の基礎
(1) 線形モデルと非線形モデルの基本的な考え方
逆推定の解析,標準誤差と信頼限界 大和田 章一
https://biostat.jp/archive_teireikai_2_download.php?id=19
最小2乗法,最尤法 線形モデル,非線形モデル 芳賀 敏郎
How the F test works to compare models GraphPadPrism Curve Fitting guide
我楽多頓陳館 第4展示室 雑学の部屋
統計学入門 杉本典夫
第2期 医薬安全性研究会
多剤用量反応実験の新たな統計解析
-薬理実験における効力比の直接算出-
福島 慎二