マイクロ磁気シミュレーションのために多面体をメッシュ化する

背景

エジンバラ大などが開発公開している簡便なマイクロ磁気シミュレーションソフトMERRILL¹について、凸多面体を単純なメッシュにする方法をまとめました。
MERRILL用のメッシュの解説^2,3は、直方体などのごく単純な形状か、実試料を三次元スキャンした画像データを用いたものしかなく、さらに英語しかないようです。ここに書いた方法で、三次元スキャンせずともCADで色々な形（磁鉄鉱の自形である八面体とか）を作って遊べると思います。
地球物理や材料科学の学生（や研究者）が、気楽にシミュレーションして磁気への興味を深めてくれるとうれしいです。真剣にやる人はもう少しちゃんとしたメッシュを作ったほうが良いのかもしれません（よくわかりません）。

0. 準備

• MERRILL
• gmsh
• octave
• bash
• python
  • meshio
  • scipy
• paraview

MERRILLは公式ページでコンパイル済みソフトが公開されています。
メッシュ生成には gmsh (4.7) を使います。ここではpython用のapiを主に使いました。pipで普通に取れます。anacondaにもあるがうまくインストールできないような・・。
後はファイル形式の変換です。MERRILLはpatranフォーマットとやらで記述されたメッシュを読むのですが、簡単にこれに変換する方法が見つかりません。コミュニティでmerrillsaveというmatlabスクリプトが作られていて、 公開されています 論文著者⁴にメールすることで手に入れられます。ファイル形式変換だけのために入れるのもアレですが、これを動かすためにoctaveを使います。そしてこの出力は正確にはpatranフォーマットになっていないそうで、再度変換するためのシェルスクリプト Convert2Pat.sh が公開されています²。ファイル形式変換だけのために（略）、Windowsならwslを入れると良いでしょう。
後は重要ではないですが、なんやかんやのためにpython (3.7) を使いました。meshioを使ってgmsh形式のファイルからメッシュ情報を取り出し、scipyでmatファイルにすると捗ります。凸包が取れるのも便利。paraviewは計算結果を可視化するのに使いました。

1. モデル生成

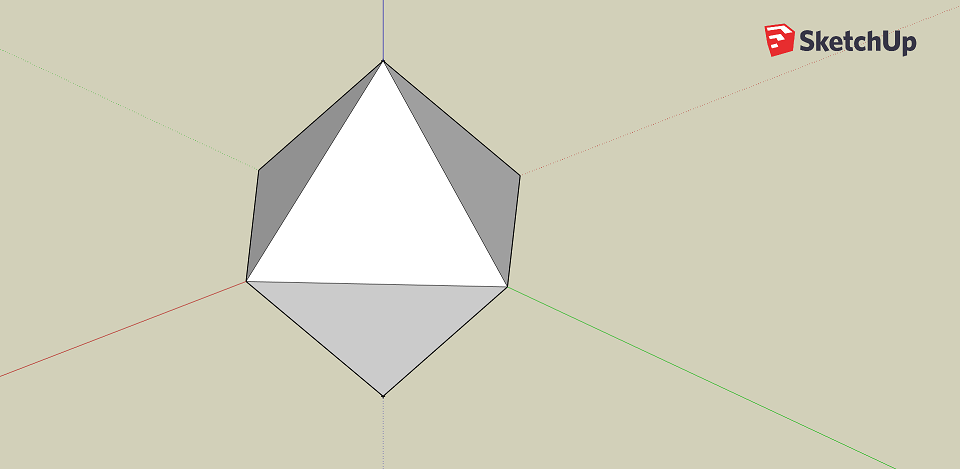
多面体のstlファイルを用意します。例えばSketchUpを使って八面体を作ってみましょう。一辺 200 (mm) として作りましたが、単位は任意なので以下では 200 nm と思って扱います。

2. メッシュ生成

gmshにstlからメッシュを作るというのがあるようなので、簡単にできるのかもしれません。ここでは真面目にやります。
gmshでは点、点を結ぶ線、線が作るループと面、面に囲まれた領域と体積、と順番に準備して、最後に体積に対してメッシュ生成をかけることで、面や線を保存したメッシュを作ります。点はstlに書いてあるものをそのまま使えますが、stlには線の情報そのものはないので、面から逆に線を作らなければいけません。また、適当にモデルを作ると多面体内部に面を作ってしまうことが往々にしてあります。そこで凸包を取ることで外部の面だけを抽出します。これらに注意すると、例えば以下のように書けるでしょう

import gmsh
import meshio
import numpy as np
from scipy.spatial import ConvexHull

stldata = meshio.read("octahedra-200nm.stl")

gmsh.initialize()

lc = 9 # メッシュサイズ (9nm)

points = [gmsh.model.geo.addPoint(p[0], p[1], p[2], lc) for p in stldata.points] # gmshに点を追加。pointsは点の名前の配列

hull = ConvexHull(stldata.points) # 凸包を取る
simplices = np.array(hull.simplices)+1 # 凸包の各面の指数。gmshは1-indexなので1を足しておく

spam = [] # 面から線を作る。2つの面で共有している線を省く。
for l in simplices:
    spam.extend([list({l[0], l[1]}), list({l[1], l[2]}), list({l[2], l[0]})])
edgepairs = []
for l in spam:
    if l not in edgepairs:
        edgepairs.append(l)
edgepairs = np.array(edgepairs) # 線の端点ペアのリスト

lines = [gmsh.model.geo.addLine(l[0], l[1]) for l in edgepairs] # 線を追加。点は名前で指示する。linesは線の名前の配列。点と名前がかぶっても良い。

def findcurve(l, edgepairs, lines): 
    '''
    抽出した線で改めて面を定義するための関数。 
    lという線（端点ペア）が与えられたとき、端点ペアのリストを参照して、保存されている線の指数で表現する
    '''
    b = (edgepairs[:, 0]==l[0]) & (edgepairs[:, 1]==l[1])
    if np.sum(b)>1:
        return 0 # 指数ゼロというのはないので、こうするといずれどこかでエラーになってくれるはず
    elif np.sum(b)==1:
        return np.where(b==True)[0][0]+1
    else:
        b = (edgepairs[:, 0]==l[1]) & (edgepairs[:, 1]==l[0])
        if np.sum(b)==0:
            return 0
        else:
            #print(np.where(b==True)[0][0])
            return -1 * (np.where(b==True)[0][0]+1) # 線の向きは符号で表現する。

loops = [] # 面の前にループという概念がある。
for s in simplices:
    l1 = findcurve([s[0], s[1]], edgepairs, lines)
    l2 = findcurve([s[1], s[2]], edgepairs, lines)
    l3 = findcurve([s[2], s[0]], edgepairs, lines)
    print([l1, l2, l3])
    loops.append(gmsh.model.geo.addCurveLoop([l1, l2, l3]))

surfaces = [gmsh.model.geo.addPlaneSurface([loop]) for loop in loops] # 凸多面体なのですべてのループに面を定める

gmsh.model.geo.addSurfaceLoop(surfaces, 100) # 一つの多面体なので、すべての面が一つの体積を囲む。100は面のループの名前（任意）。
gmsh.model.geo.addVolume([100], 101) # 面のループに体積を対応させる。101は体積の名前（任意）

gmsh.model.geo.synchronize()
gmsh.model.mesh.generate(3) # 3次元メッシュの生成

gmsh.write("octahedra-200nm.msh")
gmsh.finalize()

これでメッシュができました。

(表示はgmshアプリケーションを使用）

最後に、メッシュをoctaveで読むためにmat形式にしておきます。ここでは点をnode, 四面体メッシュをelem, 三角形メッシュを（使いませんが）faceという名前で格納します。またMERRILL内では長さ単位は $\mathrm{\mu}$mです。

import meshio
from scipy.io import savemat
m = meshio.read("octahedra-200nm.msh")

# nm -> um
node = m.points / 1000.

# matlab配列は1からなので1を足す
elem = m.cells_dict["tetra"] + 1
face = m.cells_dict["triangle"] + 1
spam = {"node": node, "elem": elem, "face": face}

savemat("octahedra-200nm.mat", spam)

3. ファイル変換

まずOctave上で

load("octahedra-200nm.mat")
merrillsavepat("octahedra-200nm_K", node, elem)

とし、次にBashで

Convert2Pat.sh octahedra-200nm_K octahedra-200nm.pat

とすると、目出度くpatファイル（のようなもの）ができました。

4. マイクロ磁気計算

試しに計算しましょう。パラメーターはこんな感じ

Set MaxMeshNumber 1

ReadMesh 1 octahedra-200nm.pat

Set MaxEnergyEvaluations 5000

ConjugateGradient
Set ExchangeCalculator 1

Magnetite 20 C
Uniform magnetization 0.99,1,1
External Field Strength 0.05 mT
External Field Direction 1,1,0.999

EnergyLog energy_log.txt

Minimize
WriteMagnetization Octahedra-200nm_log
CloseLogfile
END

これをscript.txtとして保存しておきます。
20Cの磁鉄鉱として、[111]方向に均質な磁化を初期状態とし、[111]方向に0.05mTの磁場がかかっている状態での平衡状態を探索します。
数値計算的に対称軸ジャストになにかやると具合が悪いことが多いという解説を見たので、ちょっとずらしています。
計算を実行します

merrill script.txt

だいたい2分(1000ステップ)で終了しました。

計算結果はparaviewで表示できます。

vortexですね。
細かいこと言うとz方向逆じゃないか・・という気がしますがよくわかりません。

5. 失敗（おまけ）

この方法に至るまでにいくつか失敗したので参考に載せておきます。

ケンブリッジ大グループの解説³によると、三次元スキャンはparaviewでstlにし、octave上でstlreadというので読み、iso2meshというので体積メッシュを作る、とされています。ならばSketchUpのstl出力をこう出来るのか…というと、まずstlreadで読めなかったりします。この原因は良くわかりませんが、いずれにせよ多面体のstlは表面形状と言えないほどスカスカなので、これでは多分うまく行かないでしょう。

iso2meshはCGALというC++ライブラリを利用しているようなので、その部分的なpython移植であるpygalmeshでstlから体積メッシュを作る、ということも試しました。一応できるんですが（100nmの八面体で例示）、

エッジは再現されません。多分磁気計算には影響無い予感がしますが（ある意味でより自然な形かも）、ちょっと不満です。本家CGALでは保存すべき線や面を指定できそうですが、pygalmeshは開発中ということもあり、そういうのがどうなってるのかわかりませんでした。

八面体程度なら数値的に三次元画像を作れますが、それを用いても同じような感じになります。現実の三次元スキャンは曲線で囲まれた形状を扱うので、エッジ保存はあまり問題にならないかもしれません。

1. https://agupubs.onlinelibrary.wiley.com/doi/full/10.1002/2017GC007279 ↩

2. https://www.geos.ed.ac.uk/geosciences/research/projects/rockmag ↩ ↩²

3. https://wserv4.esc.cam.ac.uk/nanopaleomag/?page_id=1778 ↩ ↩²

4. https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2019GC008761 ↩