これは何

Second-generation p-values: Improved rigor, reproducibility, & transparency in statistical analyses¹

を読んだ。良さそうだったので半分自分用のメモとして概要をまとめておく。

理解ゆるゆるなんで強者のコメント・ツッコミを期待(記事にコメント残したりしてくれると嬉しいです)
基本的にはバイオインフォマティクス分野、特に omix解析での利用可能性を想定しながら読んだ。論文の例もMicroarrayなので筆者たちも多分そのつもり。
(おそらく生物学系の読者を意識して)数学的に厳密な部分はサプリに飛ばされているが、その部分はあんまり真面目に読んでない
僕のコメントと筆者の主張が入り混じっている翻訳でも要約でもない謎文章なので疑問あったら原典へgo

tl;dr

Second-generation p-values(以下2nd-p)は帰無仮説としてある区間を設定する。得られたデータの区間(例:95%信頼区間)と帰無仮説を用いて計算し、2nd-pが1であれば帰無仮説を棄却、0であれば帰無仮説を棄却しないという判断を行う。値が0~1の間の場合は与えられた条件では判断できない(ので、帰無仮説やデータの見直しが必要)とする。
2nd-pが0であるデータ群同士の比較に関しても手法を提供。(古典的なp-valueの大小比較に対応)
多重検定補正の問題が生じない ので、omix解析においてはBonfferoni補正やFDR補正をreplaceするような位置。なので新しい多重検定補正の手法のようなものとしても捉えられる(個人的にはこれが一番アツい)

p-valueとの比較(イメージ)

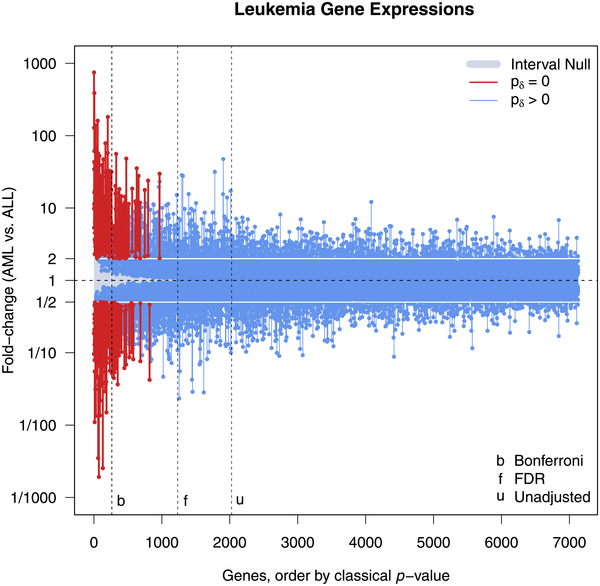
今までの p-value(上)は帰無仮説としてある一点の値を取る。
対して 2nd-p(下)は帰無仮説として区間を仮定する(区間内の確率密度などは考慮しないので、分布でなく区間)。interval nullなので以下帰無区間とする。
めちゃざっくり言うと
- overlapが存在しない場合: 2nd-p = 0 対立仮説を支持
- confidence intervalが帰無区間に収まっている場合: 2nd-p = 1 帰無仮説を支持
- それ以外の場合(部分的なoverlapが存在): 0 < 2nd-p < 1 判断不能だが2nd-pの値で上記のどちらよりかは分かる。

導出

後半部は補正なので、まずは前半部を抑える。
${I}$は得られたデータの95%信頼区間で、${H_0}$ は帰無区間。
前半部は言い換えると 「得られたデータの区間の何割が帰無区間に属するか」 という割合。
確率として扱われるp-valueとの最大の違いがここ。

p-valueとの比較

「得られたデータの区間の何割が帰無区間に属するか」なので、 2nd-p は p-valueと違い1か0の値を取れます。1なら帰無仮説を支持、0なら対立仮説を支持、と解釈する。

Study 4では式の後半部による補正が効いていて、帰無区間より95%信頼区間の方が2倍以上大きい場合(実用的にはサンプル数が少ない場合)の補正を効かせている。帰無区間に入らないデータの割合ということで0.5という値が出ているのはいいのだが、この計算だと単純に帰無区間に対してむちゃくちゃ分散でかいデータだと 2nd-p が低くなってしまいそうだが、 0 < 2nd-p < 1 の時は等しく判断不能とするため、あまり問題にならないということだと思う。

${max\ p}$ は帰無分布の中で最もp-valueが高くなる点を採用した時のp-valueを表す。Study2のようなケースだと${max\ p}$は 2nd-p と同じ値を出すけどStudy 3~6のようなケースでは 2nd-p のほうが望ましい属性を持つとのこと。

delta-gap

omix解析とかだとp-valueの値でソートしたい時とかが割とあるので、その場合は原理的に0にならない ${traditional\ p\ value}$ の方が便利そうだなと思って読んだら、それに対する対処法も書いてあった。
delta-gapは${I}$と${H_0}$の距離であり、これが離れている方がより帰無仮説から遠いという判断ができ、2nd-pが0となる複数のデータに対してランク付けを行うことができる。

後述しますが、これは直感的にp-valueの大小比較よりわかりやすい結果になりそう。

95%信頼区間で本当にいいの？

当然ですが区間は何使っても良くて、 Bayesian credible interval とか 1/8 likelihood support interval とか色々あるよねということ

多重検定補正に関して

多重検定補正やんなくてよくなるのが2nd-pの特徴で、これは2nd-pが表すものが確率でなくて割合だから。その代わり、interval nullをどう設定するかで取れてくる遺伝子の量が変わるので、ここの値の決め方が今後業界的にコンセンサスとれてくると良さそう。

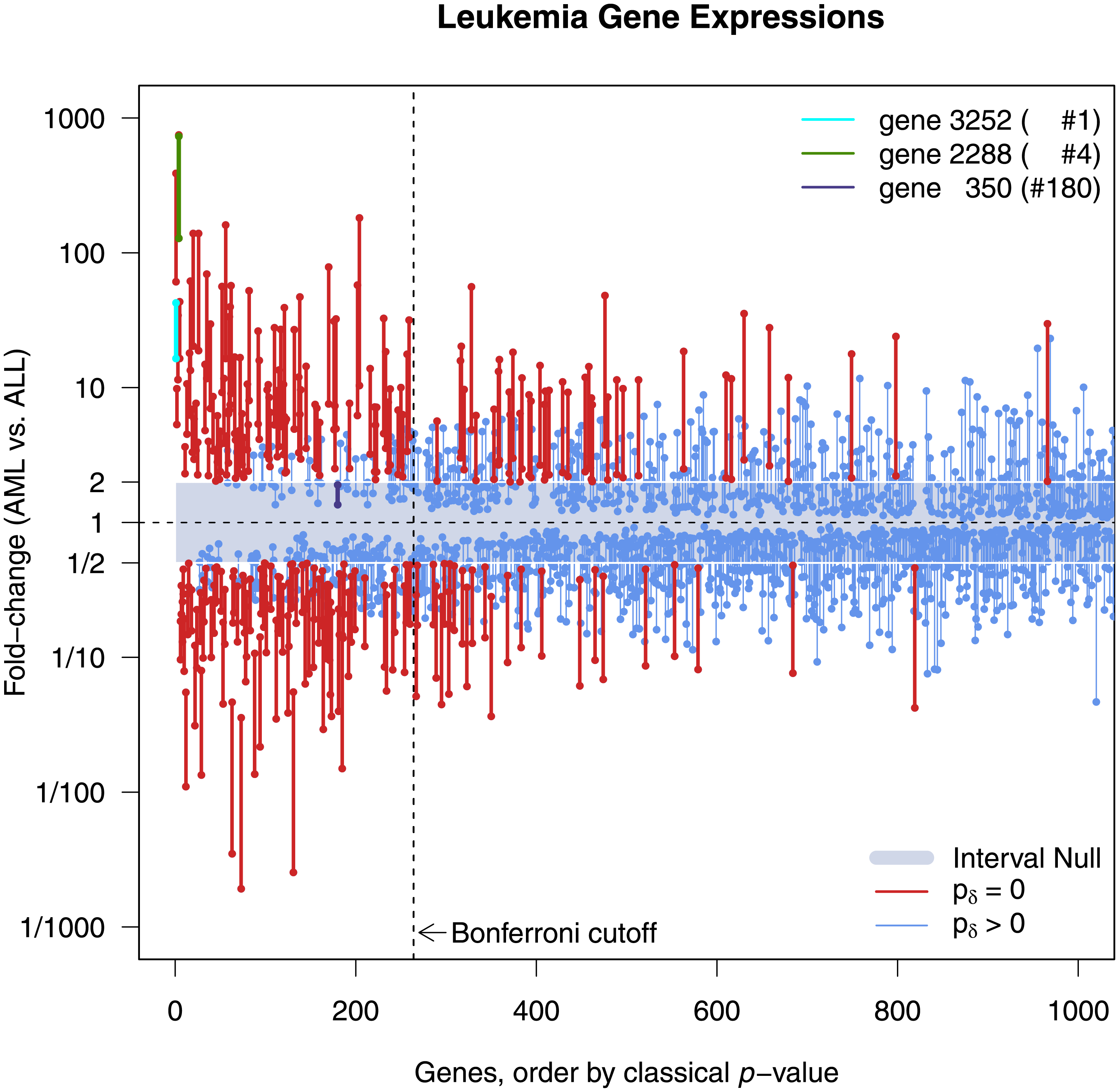
これまで(厳格な多重検定補正である)Bonferroni法で補正をかけた場合ですら生き残っていたものが2nd-pだと有意な差でないと判断されることや、その逆も結構あるようだ(無論interval nullの設定次第なのだけど)。しかし以下の例(図中に表示してあります)を見ると2nd-pの値の方が直感的で良さそう。

gene2288: p-valueでは4位だがdelta-gapだと1位
gene3232: p-valueでは1位だがdelta-gapだと10位
gene350: Bonferroniでは有意だが2nd-pだと有意じゃない

間隔の考え方が便利

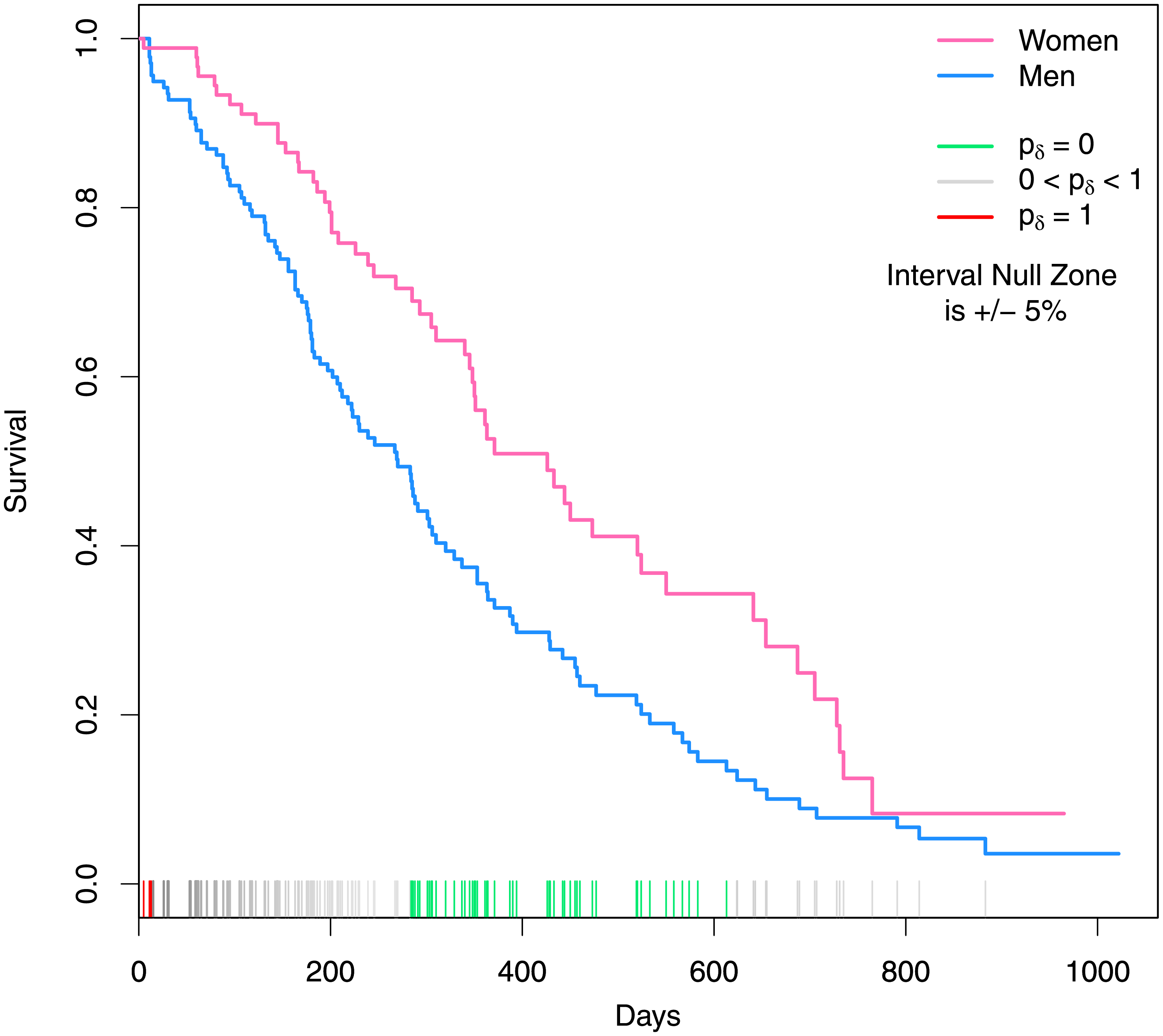
有意かどうかを間隔で考えるというのが便利で、例えば上記のような男女の生存曲線においてプラスマイナス5%の差がある時期は有意、というような使い方ができる。
多重検定補正の問題から解放されてるのがここでも役立っている。時系列データの解析は未だにややこしい問題だが、そういった解析にも強みがありそう。

2nd-pの信頼性はどうなの

2nd-pの信頼性の指標としては、FDR(偽陽性): ${(P(H0\ |\ p_δ = 0))}$ とFCR(偽陰性): ${(P(H1\ |\ p_δ = 1))}$ を使う。

それらの値は以下のように、偽陽性と偽陰性の確率はBayesの定理を用いて計算することができる。

${H_0}$: 帰無仮説
${H_1}$: 対立仮説
${r = P(H1)/P(H0)}$ : 事前確率

この式が示すのは、サンプルサイズが大きくなるとFDRもFCRも0に収束するという2nd-pの特性。これは多重検定補正において許容するFDRの値を定めるFDR法と比べても優れている(と筆者たちは言っている)が、確率の部分を95%信頼区間に押し込んだせいでFDRやFCRなどの確率の扱いに関してはむしろ多重検定補正よりも理解がむずそう(僕はまだ腑に落ちていない)。

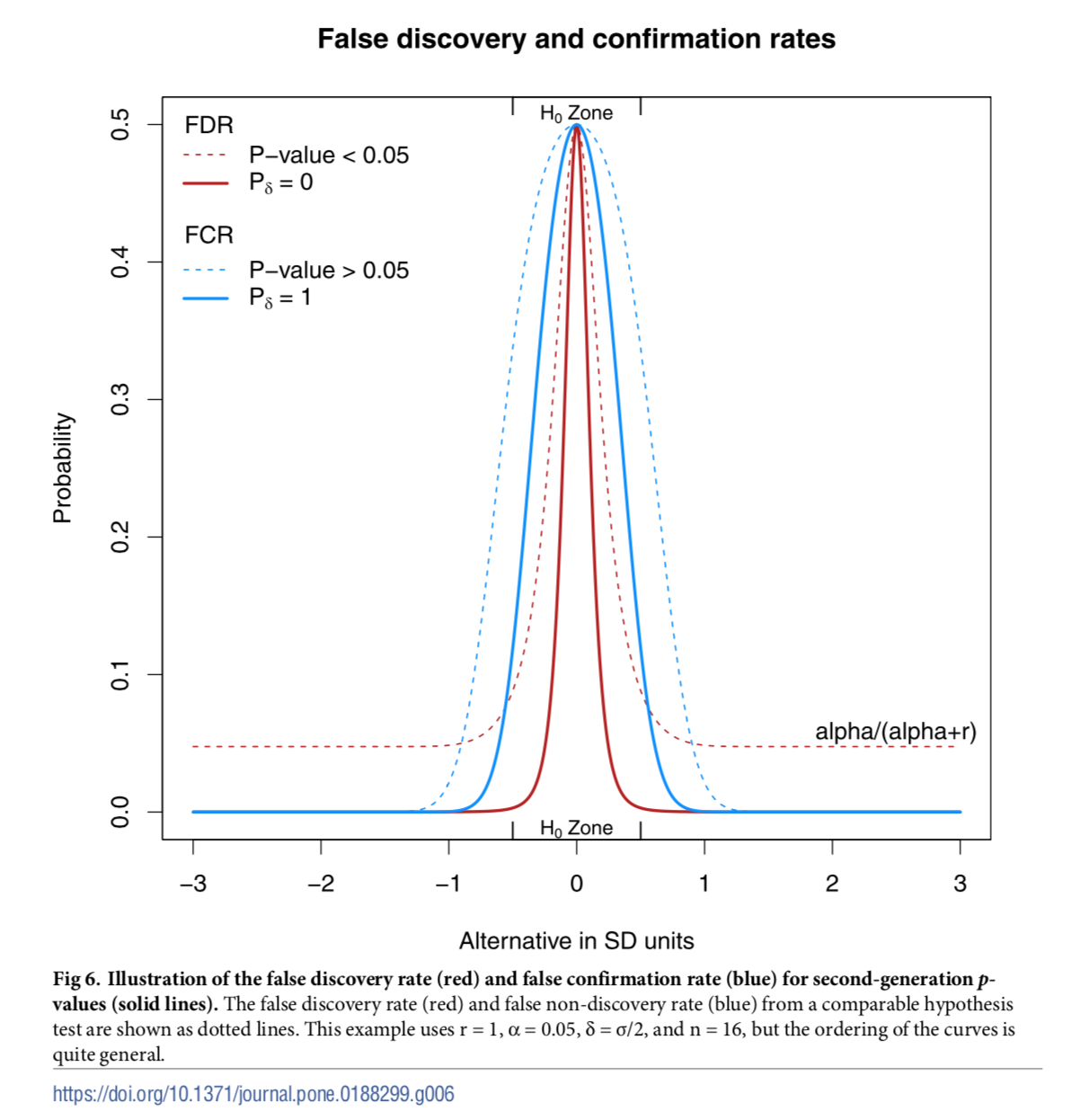
上記は旧来の仮説検定(dotted line)と2nd-p(solid line)におけるFDR、FCRを比較すると、2nd-pの方がFDRもFCRも低くなるので信頼性が高いそう。

コメントなど

いい手法ぽい。とにかく確率でなく割合で表現しているのが秀逸で、p-valueよりも直感的にわかりやすいと感じた
広く使われるためには使いやすい実装などが必要そう。本論文ではPackageの公開などはしてないっぽいが、その後（多分）第三者による検証論文が出ていて、著者がRでの実装をgithubで公開している。コード見てもわかるように計算めちゃくちゃ簡単なので、自分で実装しちゃうのが楽そう。DEG検出のソフトウェアとかに組み込まれると爆発的に普及しそう。
この手の話はレビュアー次第なところもあるので、しばらくは今まで通りの多重検定補正と併用することになるのかな。まだあんまり引用されていないっぽいので、今後の展開にも期待。

Blume, J. D., McGowan, L. D. A., Dupont, W. D., & Greevy Jr, R. A. (2018). Second-generation p-values: Improved rigor, reproducibility, & transparency in statistical analyses. PloS one, 13(3), e0188299.ISO 690. ライセンスがCC-BYなので、著者と原典を明記すれば自由に改変/公開OK ↩

多重検定補正が要らなくなる、Second-generation p-values が良さそう