MiniSearch という軽量な全文検索ライブラリがあったので、ソースコードを読んでみた まとめ。
MiniSearch とは?
Javascript で書かれた軽量の全文検索ライブラリ。
作者の Luca Ongaroさん が、サーバーサイドでの全文検索(N-gram など)で検索するとレイテンシーの関係でユーザービリティが良くないと思い、フロントエンドで全文検索(Radix木)してみたいと思って書いたライブラリ。
デモは、こちら。
MiniSearch には 全文検索のみならず 自動サジェスチョンなどの機能があります (日本語対応はしてないそうです) が、この記事では、全文検索部分のみに焦点を当てて説明します。
(気が向いたら、続きも書きます。)
※ もし内容が難しかったら、MiniSearch の バージョン1 の方が読みやすいので、参考にしてもいいかもしれません。
全文検索の実装部分は、主に SearchableMap という名前で実装されています(ソースコードはこちら)。
この SearchableMap フォルダの SearchableMap.ts に実装が載っています。
早速コードへ ... の前に
早速コードに、の前に前提知識が必要になります。
その前提知識が、Radix 木 と Levenshtein 距離 の2つになります。
Radix木
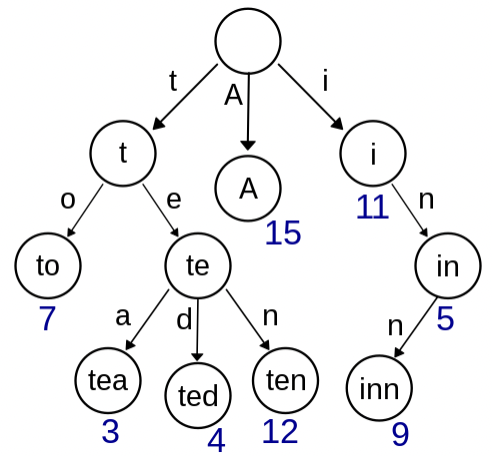
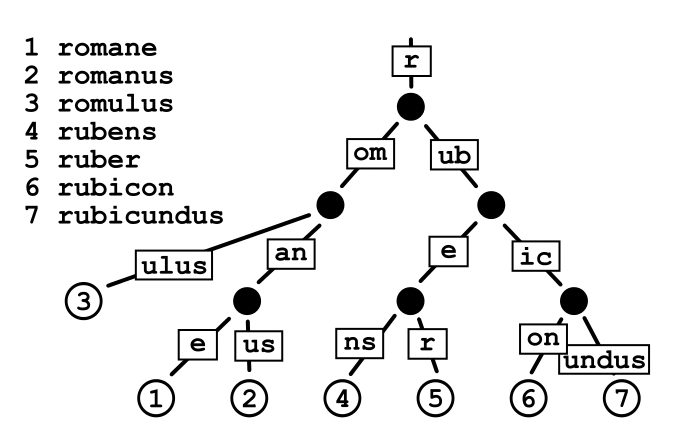
Radix 木は Trie木 が 1文字ずつなのを、複数の単語でひとまとめにしたノードを持つように改良した木構造のことです。Trie木 とは、単語を1文字ずつにして、それを各ノードが1文字ずつ分かれ目になっている木構造のことです(下の図を見ると分かりやすいと思います)。
Radix 木は、再度になりますが、単語が1文字分割ではなく複数の文字がノードを構成しています。
他の記事を見れば分かりますが、全探索よりも早く単語を見つけることができます。
Trie木の実装は、ここ などにあるように難しくないですが、
Radix木 となると Insert の時に 中間ノードを作って分割する必要があったり(コードはここ)、Delete の時にノードをマージさせる分岐が必要になる(コードはここ)ので、少し複雑になります。
Levenshtein 距離
Levenshtein 距離とは 2つの文字列の違いを数字で表したものです。
違いの計算方法は、
1:単語A + 1 x 単語B + 1 の行列X を作ります。
2:行列X の最初の行と最初の列を0からの昇順にします。
3:行列X の数字が決まっていない 1つ1つの要素を 上+1と横+1と斜め上(対応する単語Aと単語Bが同じ場合はそのまま、違う場合は +1)のうち一番大きいものにします。
4:1つ1つの要素が全て3の計算を終えたら、右下の数字を見ます。それが単語間の距離になります。
Python で実際に実装してみたのが、下の実装になります。
def levenshtein(a, b):
a_len = len(a)
b_len = len(b)
max_distance = max([a_len, b_len])
matrix = [[max_distance for i in range(b_len+1)] for j in range(a_len+1)]
for i_index, i in enumerate(range(a_len)):
matrix[0][i_index] = i_index
for j_index, j in enumerate(range(b_len)):
matrix[j_index][0] = j_index
#
for i in range(1, a_len+1):
a_c = a[i-1]
for j in range(1, b_len+1):
b_c = b[j-1]
m = matrix[i][j-1] + 1
n = matrix[i-1][j] + 1
l = 0
if (a_c == b_c):
l = matrix[i-1][j-1]
else:
l = matrix[i-1][j-1] + 1
min_distance = min([m, n, l])
matrix[i][j] = min_distance
print(matrix[a_len][b_len])
levenshtein("meilenstein", "levenshtein")
では、前提知識もついたので、コードを読んでみましょう!
コードを読んでみる
まずは、SearchableMap の本体がありそうな SearchableMap.ts を見てみます。
すると、clear, delete, get, set など基本的な関数が意外と短い行で書いてあるのが分かります。
set を例に取ったら、下の行のみになります。
set (key: string, value: T): SearchableMap<T> {
if (typeof key !== 'string') { throw new Error('key must be a string') }
this._size = undefined
const node = createPath(this._tree, key)
node.set(LEAF, value)
return this
}
この createPath というのが何かしてそうですね。
中身を見てみましょう。
const createPath = <T = any>(node: RadixTree<T>, key: string): RadixTree<T> => {
const keyLength = key.length
outer: for (let pos = 0; node && pos < keyLength;) {
for (const k of node.keys()) {
// Check whether this key is a candidate: the first characters must match.
if (k !== LEAF && key[pos] === k[0]) {
const len = Math.min(keyLength - pos, k.length)
// Advance offset to the point where key and k no longer match.
let offset = 1
while (offset < len && key[pos + offset] === k[offset]) ++offset
const child = node.get(k)!
if (offset === k.length) {
// The existing key is shorter than the key we need to create.
node = child
} else {
// Partial match: we need to insert an intermediate node to contain
// both the existing subtree and the new node.
const intermediate = new Map()
intermediate.set(k.slice(offset), child)
node.set(key.slice(pos, pos + offset), intermediate)
node.delete(k)
node = intermediate
}
pos += offset
continue outer
}
}
// Create a final child node to contain the final suffix of the key.
const child = new Map()
node.set(key.slice(pos), child)
return child
}
return node
}
ぱっと見た感じでは何をやっているのかよく分かりませんね。
なので、少し説明を加えます。
まず、このコードでは、
入力された登録をする単語を、現在のノードの Radix木の子要素1つ1つと比較して、
1:比較結果が 現在の単語が Radix木の子要素に含まれている場合は、含まれる分までの単語を位置情報として取得します (offset)。そして offset の大きさに応じて、木を分割する or そのまま で 次の node に分割されたかそのままのノード を渡しています。そして 登録をする単語のポインターを offset 分だけ増やして、次のループに入ります。
2:比較結果が 現在の単語が Radix木の子要素に含まれていない場合(最後の場合)は、そのまま複数単語になりうる単語を node に格納します。
のようなことをしています。
要は単語を比較して、どちらにも含まれている分だけノード(分割する場合もある)を作るループを繰り返して、単語を木構造に登録しています。
一番厄介な 登録部分は上のようになっていました。
では、参照はどうなっているのでしょうか?
先ほどと同じく get という関数を見てみましょう。
get (key: string): T | undefined {
const node = lookup<T>(this._tree, key)
return node !== undefined ? node.get(LEAF) : undefined
}
Lookup という関数が何かしていますね。
const lookup = <T = any>(tree: RadixTree<T>, key: string): RadixTree<T> | undefined => {
if (key.length === 0 || tree == null) { return tree }
for (const k of tree.keys()) {
if (k !== LEAF && key.startsWith(k)) {
return lookup(tree.get(k)!, key.slice(k.length))
}
}
}
再帰的なコードになっていて分かりづらいですね。
紛らわしいのが、lookup にある tree.get(k) というのが、createPath で登録した new Map の get であるということでしょうか。
tree の keys に LEAF (単語が登録されたキー) が出てくるまで lookup を繰り返し、最終的に返された node の LEAF を返しています。
他にも、削除(remove) などの関数もあります。興味があったら、見てみてはいかがでしょうか?
FuzzyGet
ここまでで、登録 (set) と 取得 (get) を見てみました。
この他にもこのライブラリには、近い単語を探す機能があります。それが FuzzyGet です。
ファイルとしては、fuzzySearch.ts にあります。
ここで、前提知識で書いた Levenshtein 距離が 出てきます。
では、コードを読んでみましょう。
まず Levenshtein 距離では、1列目・1行目が0からの昇順になったマトリックスを作ります。それが下の部分です。
const n = query.length + 1
// Matching terms can never be longer than N + maxDistance.
const m = n + maxDistance
// Fill first matrix row and column with numbers: 0 1 2 3 ...
const matrix = new Uint8Array(m * n).fill(maxDistance + 1)
for (let j = 0; j < n; ++j) matrix[j] = j
for (let i = 1; i < m; ++i) matrix[i * n] = i
この後で、この matrix などを使い recurse という関数を呼んでいます。
recurse の中身は、LEAF の分岐以外は、Levenshtein 距離の実装そのままですね。
// Iterate over remaining columns (characters in the query).
for (let j = jmin; j < jmax; ++j) {
const different = char !== query[j]
// It might make sense to only read the matrix positions used for
// deletion/insertion if the characters are different. But we want to
// avoid conditional reads for performance reasons.
const rpl = matrix[prevRowOffset + j] + +different
const del = matrix[prevRowOffset + j + 1] + 1
const ins = matrix[thisRowOffset + j] + 1
const dist = matrix[thisRowOffset + j + 1] = Math.min(rpl, del, ins)
if (dist < minDistance) minDistance = dist
}
3つの数字から最も小さいものを選択しているのが分かるでしょうか?
この後で面白いのが、
if (minDistance > maxDistance) {
continue key
}
}
recurse(
node.get(key)!,
query,
maxDistance,
results,
matrix,
i,
n,
prefix + key
)
で、距離が大きすぎる場合は、ループから脱出していることです。
逆に言えば、距離が小さければ、再度再帰的に探索を続けています。
これで、root のいくつかのノードの計算とそこから深く探索するだけの計算量になっているのが分かります。
感想
最初は難しかったけど、読んでみると理解できて良かった。
別の全文検索ライブラリも読んでみたい。