はじめに
ヨビノリさんの「相加相乗平均の関係」を視覚的に理解する!という動画が人気みたいなので僕も別のを考えてみました。
相加平均≧相乗平均とは?
任意の非負の実数$V_1,V_2$に対して
$$
\frac{V_1+V_2}{2} \geq \sqrt{V_1V_2}, (1)
$$
が必ず成り立つという不思議な定理です。
数学的な説明
簡単です。$V_1,V_2 \geq 0$なので、(1)式の両辺は非負です。従って、両辺を二乗しても大小関係は変わりませんから、両辺を2乗して
$$
\frac{\left (V_1+V_2 \right)^2}{4} \geq V_1V_2
$$
を得ますが、これを計算して整理すると
$$
(V_1-V_2)^2 \geq 0
$$
という必ず成立する式になるので、(1)式は必ず成り立つことが分かります。
視覚的な説明
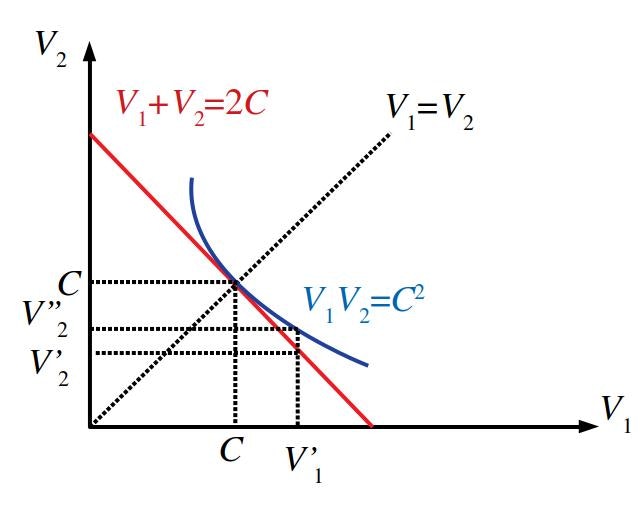
まず任意の非負の実数$C\geq0$に対して、
$$
V_1 + V_2 = 2C
$$
というグラフを描きます(図の赤い直線)。次に
$$
V_1V_2=C^2
$$
というグラフを描きます(図の青い曲線)。この2つの曲線は$V_1=V_2=C$のところで接します。なぜなら
$$
\frac{C+C}{2} = C = \sqrt{C^2}
$$
だからです。次に$V_1'\neq V_2', V_1' + V_2'=2C$である$V'_1,V'_2$を考えます。また$\sqrt{V_1'V_2''}=C$になるような$V_2''$を考えます。明らかに$V_2''>V_2'$なので$\sqrt{V_1'V_2''} \geq \sqrt{V_1'V_2'}$なので
$$
C= \frac{V_1' +V_2'}{2} = \sqrt{V_1'V_2''} \geq \sqrt{V_1'V_2'}
$$
だということが分かります。これで相加平均≧相乗平均が説明できました。
3乗の場合
この視覚的な説明のよいところは簡単にn乗の場合に拡張できることです。$n=3$の場合を考えてみましょう。
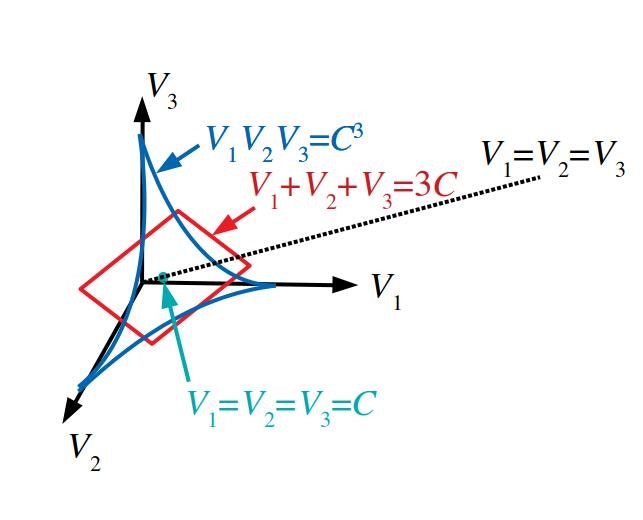
$V_1+V_2+V_3=3C$が赤い四角で囲まれた平面、$V_1V_2V_3=C^3$が青い曲線で囲まれた曲面です。両者が接するのは$V_1=V_2=V_3=C$です(緑の点)。「青い曲線で囲まれた曲面」は「赤い四角で囲まれた平面」よりも「手前」(座標原点が無い側の空間)に属しています。これさえ解ればあとは全く同じ議論が使えます。
$V_1'+V_2'+V_3'=3C$になる$V_1',V_2',V_3'$に対し$V_1'V_2'V_3''=C^3$となるような$V_3''$を考えたら、$(V_1',V_2',V_3'')$は$(V_1',V_2',V_3')$より「手前」にあるので$V_3''>V_3'$でなくてはなりません。従って
$$
C = \frac{V_1'+V_2'+V_3'}{3} = \left (V_1' V_2' V_3'' \right) ^{1/3} \geq \left (V_1' V_2' V_3' \right) ^{1/3}
$$
となって$n=3$の時の相加平均≧相乗平均が証明出来ました。
n乗の場合
$n\geq4$については絵を描くことはできませんが、一般に
「$\sum_{i=1}^n V_i = nC$という超平面Aと$\prod_{i=1}^n V_i =C^n$という超曲面Bは$V_i=C$で接する」
という事実と
「超曲面B上の点は超平面A上の点より必ず原点から遠い位置にある」
という事実さえ認識できれば、
$$
nC = \sum_{i=1}^n V'_i
$$
および
$$
C^n=\left (\prod_{i=1}^{n-1} V_i' \right) V_n''
$$
であれば
$$
V_n'' \geq V_n'
$$
となるので
$$
C= \frac{\sum_i V_i'}{n} = \left [ \left( \prod_{i=1}^{n-1} V_i' \right)V_n'' \right ]^\frac{1}{n} \geq \left [ \left (\prod_{i=1}^n V_i'\right) \right ]^\frac{1}{n}
$$
であることが言えて$n$乗の時の相加平均≧相乗平均が「視覚的に」説明できます。
おわりに
n乗の場合の相加平均≧相乗平均を「視覚的に」説明してみました。