1 主成分分析は線形手法?
世の中的には「非線形データを扱うときは主成分分析ではだめ」というのが通り相場になっている。しかし、Unsupervised Feature Extraction Applied to Bioinformaticsと題する本を昨年出版し、バイオインフォマティクスに主成分分析を用いた解析の論文を一杯出している僕としては「生命現象って非線形データの最たるものでは?」という思いがあり、内心、忸怩たる思いがある。主成分分析が非線形データ解析に適してないなら、なんで僕は一杯論文を書けたのか?そこで、ここでは簡単な例で「主成分分析が非線形データに弱い」というのは一種の「迷信」であることを主張したい。
2 円の主成分分析
まず円を考えよう。具体体には$x_{i1} = \cos \left ( 2 \pi \frac{i}{N} \right) \in \mathbb{R}^N$,$x_{i2} = \sin \left ( 2 \pi \frac{i}{N} \right) \in \mathbb{R}^N$,みたいなことを考える。
N<-100
theta <- seq(0,2*pi,length=100)
x <- cbind(cos(theta),sin(theta))
plot(x)
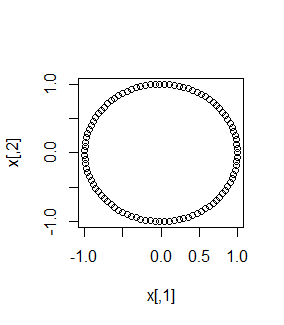
こんな感じである。ここで点$i_1$と点$i_2$のユークリッド距離行列$d_{i_1 i_2} = \sqrt{\sum_{j=1}^2 (x_{i_1j} -x_{i_2j})^2} \in \mathbb{R}^{N \times N}$を考え、これに特異値分解を適用してみましょう。
D <- data.matrix(dist(x))
SVD<- svd(D)
plot(SVD$u[,2:3])
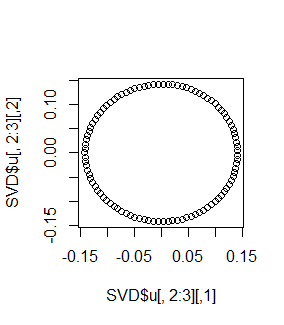
あれ、おかしいですね?円が再現されています。距離に直した段階で「非線形データ」になってしまったのだから、円は再現されないのではなかったでしたっけ?
いやいや、これは、ユークリッド距離だからでしょう? 二乗とって平方根だから結局、ほぼ線形の依存性だから。そうですね、じゃあ、$d^2_{ij}$を特異値分解してみましょう!
SVD2 <- svd(D^2)
plot(SVD2$u[,2:3])
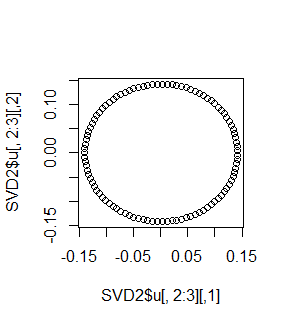
へんですね。やっぱり円が再現されています。主成分分析は非線形データを扱えないというのは嘘だったんでしょうか?
いやいや、これは円みたいなものだからでしょ?もっと複雑だったらだめなのでは?
3 正規分布に従う乱数の主成分分析
そうですね、じゃあ、100個の正規乱数を並べて、ユークリッド距離行列を作って2乗してから特異値分解をしてみましょう。さすがにここまでやったらダメなのでは?
set.seed(0)
ran <- matrix(rnorm(200),ncol=2)
SVD0 <- svd(ran)
D2 <- data.matrix(dist(ran))
SVD3 <- svd(D2^2)
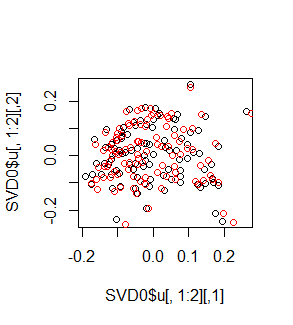
plot(SVD0$u[,1:2])
points(SVD3$u[,2],-SVD3$u[,3],col=2)
黒が元データ、赤が「ユークリッド距離行列を作って2乗してから特異値分解」の結果です。見事に再現していますね?
ということで「主成分分析が非線形データを扱えない」というのは迷信だということがよくわかりましたね?
ありがとうございました!