【Python】MuJoCo/actuatorドキュメント【MuJoCoチュートリアル②】

　本記事では、無料のオープンソース物理エンジンであるMuJoCoの<actuator>要素について解説を行います。記述はバージョン3.1.3（Python: mujoco 3.1.3）に基づきます。

　本記事はXML Referenceに基づくmujoco/actuatorの説明を中心に、具体例や検証などを併せた内容となっています。他のMJCF要素およびmjModel&mjData構造体などについてはあまり取り扱いません。別記事を参照してください。

サイズの大きい表はスタイルが崩れやすいため、画像として掲載しています。テキストとして見たい場合は、その下の「表をテキスト形式で見る」を押してください。

目次

• 目次
• はじめに
  • 本記事の数式について（変数/記号の説明等）
• 概要 : actuator (MJCF)
  • アクチュエータの種類
  • アクチュエータの制御
• 属性 : actuator (MJCF)
• actuator詳説 : アクチュエータショートカット
  • 各ショートカットごとの指定する（べき）属性
  • 各アクチュエータの詳細
• 重要なパラメタ等
  • gear
  • lengthrange
  • 力の制限
• actuator詳説 : アクチュエータモデル
  • アクチュエータ出力の算出手順
• actuator詳説 : トランスミッション
  • 概要：トランスミッション
  • トランスミッションタイプとアクチュエータ長/速度
  • トランスミッションの計算
  • joint/tendonトランスミッション
  • slider-crank トランスミッション
  • bodyトランスミッション
  • siteトランスミッション
• actuator詳説 : 活性化ダイナミクス
• actuator詳説 : 力生成メカニズム
• アクチュエータモデルのまとめ
• muscle (MJCF/actuator)
• 参考文献

はじめに

　本記事では、MuJoCoの物理エンジンにおいて重要な役割を果たす<actuator>要素について詳しく解説します。MuJoCoの基本的な概念や文法については、以下の記事で説明済みですので、本記事ではそれらの知識を前提として進めます。

本記事の読み方

• MuJoCoの基礎知識を習得したい方
  • まず前の記事を読んでから本記事を読むことをお勧めします
• MuJoCoの基礎知識はあり、<actuator>要素について学びたい方
  • 概要 : actuator (MJCF)節と属性 : actuator (MJCF)節を重点的に読むとよいでしょう。入力と出力の関係については、アクチュエータモデルのまとめ節も参考にしてください
  • また、実装に難のあるいくつかの種類については、その実装例も記述しました。slider-crankトランスミッション、bodyトランスミッション、siteトランスミッションを参照してください。
• <actuator>の基礎的な知識はあり、制御入力と出力トルク/力との関係を詳しく知りたい方
  • アクチュエータモデル以降の節をお読みください。この部分では、制御入力が出力トルク/力に変換される過程（トランスミッション→活性化ダイナミクス→力生成メカニズム）を詳しく説明しています。記述が長いため、必要に応じて参照するスタンスで構いません

本記事の数式について（変数/記号の説明等）

　以下に本記事で使用する変数の一覧とその説明を示します。書き換えが推奨されないものには括弧をつけています（参照する分には問題ありません）。関連属性が存在する場合は基本的にメンバ変数は記述していません。また、 $i$ 等の序数はほとんど $0$ 始まりです。すなわち、gainprm="1 2 3"と設定した場合は $gain_0 = 1$ となります（実際の配列との互換性のためです）。

【本記事で使用する変数・記号の一覧と説明】

変数等	関連属性・メンバ変数： 説明
$|\cdot|$	何らかのベクトル $\pmb{v}$ の長さ $|\pmb{v}|$ （→L2ノルム $\sqrt{\sum_i v_i^2}$ ）を示します。
$h$	関連属性等：mjModel.opt.timestep シミュレーションのタイムステップ幅 $h$ です。
$n_u$ $n_v$	関連属性等：（ $n_u$ : mjModel.nu, $n_v$ : mjModel.nv） 　モデル内のアクチュエータの数 $n_u$ と、自由度の数 $n_v$ です。
$\nabla$	関連属性等： なし 　勾配です。一般化座標を $q_i$ $(i=0,1,...,n_v-1)$ としたとき、 $\nabla$ は以下のように表されます。 　　 $\nabla = \left[\frac{\partial}{\partial q_0}\space \frac{\partial}{\partial q_1}\cdots \frac{\partial}{\partial q_{n_v-1}}\right]^\mathsf{T}$ 例えばモデル内にヒンジジョイント１つとスライドジョイント２つが存在した場合、 $\nabla = \left[\frac{\partial}{\partial \theta}\space\frac{\partial}{\partial x_1}\space\frac{\partial}{\partial x_2}\right]^\mathsf{T}$ などと書けます。実際には、各要素はMJCFモデルで定義された順に並びます。
$u_i$	関連属性等： mjData.ctrl[i] $i$ 番目のアクチュエータに加えられる制御入力です。
$w_i$	関連属性等：（内部状態 $w_i$ mjData.act[j] ※j番目） 　　　　　　（内部状態の変化分 $\dot{w_i}$ mjData.act_dot[j] ※j番目） $i$ 番目のアクチュエータの活性化状態です。
$p_i$	関連属性等：（mjData.actuation_space[i]） 　アクチュエータの出力トルク $\mathrm{[Nm]}$ /力 $\mathrm{[N]}$ です。 　これとは別にmjData.qfrc_actuatorも存在します。このメンバはアクチュエータが接続対象の各自由度に加えた力を示しており、要素数や対応関係はmjData.qposに同じです。
$l_i, l_i(q)$ $\dot{l_i}$	関連属性等：（アクチュエータ長 $l_i$ mjData.actuator_length[i]） 　　　　　　（アクチュエータ速度 $\dot{l_i}$ mjData.actuator_velocity[i]） 　 $l_i,l_i(q)$ は $i$ 番目のアクチュエータの各ステップでのアクチュエータ長です。ふつう対象の変位/角度とは一致しません。また、一般にbody/siteトランスミッションでは $l_i=0$ です。 　 $\dot{l_i}$ は $i$ 番目のアクチュエータの各ステップでの速度/角速度です。ボールジョイントやsiteアクチュエータ等、複数の自由度を持つオブジェクトを対象とするアクチュエータの場合、gear属性で指定した軸についての速度/角速度にのみ着目します。siteトランスミッションおよびjointトランスミッション節に詳しいです。
$\pmb{gear}$ $gear_i$	関連属性等：<actuator>→gear gear属性を $\pmb{gear}$ で、その $i$ 番目の要素を $gear_i$ で表します。特に指定がなければ注目しているアクチュエータのものを指します。
$\pmb{dyn}$ $dyn_i$	関連属性等：<actuator>→dynprm （活性化パラメタ）dynprm属性を $\pmb{dyn}$ で、その $i$ 番目の要素を $dyn_i$ で表します。特に指定がなければ注目しているアクチュエータのものを指します。
$\pmb{gain}$ $gain_i$ $Gain$	関連属性等： ゲインパラメタ $\pmb{gain}$ <actuator>→gainprm 　　　　　　 ゲイン(係数) $Gain$ gainprm属性を $\pmb{gain}$ で、その $i$ 番目の要素を $gain_i$ で表します。また、各ステップのゲインの計算結果は $Gain$ で表します。特に指定がなければ注目しているアクチュエータのものを指します。
$\pmb{bias}$ $bias_i$ $Bias$	関連属性等： バイアスパラメタ $\pmb{bias}$ <actuator>→biasprm 　　　　　　 バイアス項 $Bias$ biasprm属性を $\pmb{bias}$ で、その $i$ 番目の要素を $bias_i$ で表します。また、各ステップのバイアス項の計算結果は $Bias$ で表します。特に指定がなければ注目しているアクチュエータのものを指します。
$acc0_i$	関連属性等：（mjModel.acc0[i]） $i$ 番目のアクチュエータにおける、mjModel.qpos0での単位力からの加速度です。

※mjData.act[j]などのj番目：例としてモデル内でアクチュエータを10個定義し、そのうち内部状態（活性化状態）を持つものが３つの場合、mjData.actの要素数は３となります（mjData.ctrlなどの要素数は10）。したがって、アクチュエータの番号 $i$ と活性化状態の番号 $j$ は異なる値を取ることがあります。

本記事では何度か積分が用いられますが、"filterexact"の積分を除き基本的にオイラー法による数値積分です。"filter exact"は厳密な積分（exact integrator）により積分を行います。ただし、活性化状態の初期状態は $w_i=0\space(t=0)$ です。それぞれ以下の式により計算されます。ここで、時定数 $\mathtt{t}$ はdynprmの第１要素 $dyn_0$ です。

• 数値積分 : $x_{t+1} = x_t + h\dot{x_t}$
• exactの方 : $x_{t+1} = x_t + \dot{x_t}(1-e^{-h/\mathtt{t}})$

どちらも極限 $h\to 0$ で同じ値に収束します。前者は $\mathtt{t} < h$ で発散する一方、後者はどんな $\mathtt{t} > 0$ においても安定するという特徴があります。

概要 : actuator (MJCF)

　アクチュエータはMuJoCoの特徴的な要素のうちの一つです。<sensor>や<tendon>などと同様に、アクチュエータも<actuator>というグルーピング要素とその下の具象要素から構成されます。各アクチュエータは単一入力単一出力（SISO）システムです。PD制御などで2つ以上の制御入力が必要な場合は、複数のアクチュエータを同じ対象に接続する必要があります。

アクチュエータの種類

　MuJoCoには非常に柔軟ですべての種類のアクチュエータを作成できる<general>と、よく使われるアクチュエータのショートカット要素（アクチュエータショートカット、<motor>等９種）が用意されています。前者は設定項目が多く扱いづらいため、基本的には後者を使うことになるでしょう。

　アクチュエータを接続できる対象は、以下の4種類の要素です。アクチュエータの種類によって接続可能な対象が異なります。各アクチュエータの詳細と接続対象は下表「MuJoCoで使用可能なアクチュエータ要素」にまとめています。

• <joint> : joint属性 or jointparent属性で指定
• <tendon>: tendon属性で指定
• <body> : body属性で指定
• <site> : site属性 or refsite属性 or cranksite&slidersite属性で指定

表 MuJoCoで使用可能なアクチュエータ要素．各要素のリンク先には詳細を記述しています

要素	説明
general	接続対象: <joint>,<tendon>,<site>,<body> すべての種類のアクチュエータを作成できる最も汎用的な要素です。 これを除いた他のアクチュエータ要素はショートカットであり、dynprm～biastype＆dynprm～biasprmの6種パラメタ(等)を自動で調整したものです。
motor	接続対象: <joint>（,<tendon>,<site>,<body>） DD(ダイレクトドライブ)モータです。 実際には、制御入力と出力トルク/力が（単位を除き）一致するアクチュエータ要素です。
position	接続対象: <joint>,<site>（,<tendon>） ポジションサーボです。 物体の把持などの位置決め制御に用いられます。現在位置と目標位置の差に基づいてトルクを連続的に調整し、ジョイントを所望の位置へ駆動させます。また、slider-crankトランスミッション（簡易なスライダークランク機構）を使用する場合は一般にこのショートカットを使用します。
velocity	接続対象: <joint>（,<tendon>,<site>,<body>） 速度サーボです。 ホイールの回転制御など、関節速度の維持が重要なケースに使用します。所望の関節速度を達成するように、現在のジョイント速度と目標速度の差に合わせてトルクを連続的に調整します。
intvelocity	接続対象: <joint>（,<tendon>,<site>,<body>） 積分速度サーボです。 <velocity>が速度に直接フィードバックを返すのに対し、<intvelocity>は積分器と位置フィードバックを統合しています。制御性の維持のため、actrangeの設定が要求されます。
damper	接続対象: <joint>（,<tendon>,<site>,<body>） アクティブダンパーです。 出力 $p_i$ は速度 $v_i$ と制御入力 $u_i>0$ に負比例（ $p_i=-k_v\times v_i\times u_i$ ）します。 $k_v>0$ は速度フィードバックゲインです。 💡使用時はoptionのintegrator属性をimplicitまたはimplicitfastにすることが推奨されます。
cylinder	接続対象: <joint>（,<tendon>,<site>,<body>） 空気圧シリンダまたは油圧シリンダをモデリングするのに使用します。
muscle	接続対象: <tendon>,(<joint>) 筋肉を模したアクチュエータです。
adhesion	接続対象: <body> 吸着力を発生させるアクチュエータです。ヤモリの足や吸盤などをシミュレートできます。 吸着力は接触面積に比例しません。
plugin	接続対象: 様々 ユーザ定義のアクチュエータを使用できる、engine pluginに関連したアクチュエータ要素です。詳細はリンク先を参照してください。

実際のところ、MuJoCoには<general>以外のアクチュエータ型は存在せず、他の要素はすべて<general>のショートカットにすぎません。各ショートカットには独自の属性がありますが、内部的には<general>の共通属性に変換されます。例えば<position>のkp属性は、gainprmとbiasprmを調整するのに使われます。つまり、<general>の属性を適切に設定すれば、どのようなアクチュエータ/ショートカットも作成可能です。

アクチュエータの制御

　アクチュエータへの制御入力はmjData.ctrlを通して行います。mjData.ctrlには、MJCFファイル上で定義された順番で各アクチュエータへの制御入力が格納されています。プログラム上でこれらの値を書き換えることでアクチュエータを制御します。デフォルトではすべての制御入力は0になっています。

　例として、１つの<motor>アクチュエータを持つモデルを示します。このモデルはヒンジジョイントとカプセルボディから構成されており、<motor>アクチュエータが接続されています。初期状態では重力に任せて落下するようにしてあり、1秒経過したタイミングで逆方向の制御入力を入れることを考えます。

　制御入力の初期値は $0$ なので、初期状態ではモータにトルクは生じません。制御入力の変更はmjData.ctrlから行い、１秒経過したタイミングで $-100$ を入力します。今回はアクチュエータが"hmotor"１つのみなので、0番目の要素が"hmotor"の制御入力となります。実装の詳細は以下の「実装コードの詳細」を参照してください。

図 モータの接続された回転体．1秒以降は制御入力 $u_i=-100$

"hinge"ジョイントの軸ベクトルが $(0,1,0)$ なので、反時計回り方向への力を与えたいときの制御入力は負の値となります。

【実装コードの詳細】

m_pendulum.xml

<mujoco>
  <asset>
    <texture type="skybox" builtin="gradient" rgb1="1 1 1" rgb2=".6 .8 1" width="256" height="256"/>
  </asset>

  <worldbody>
    <camera name="fixed" pos="0 -5 0" xyaxes="1 0 0 0 0 1"/>
    <body>
      <joint name="hinge" type="hinge" axis="0 1 0"/>
      <geom type="capsule" size=".03" fromto="0 0 0 1 0 1"/>
    </body>
  </worldbody>

  <actuator>
    <motor name="hmotor" joint="hinge" gear="1"/>
  </actuator>
</mujoco>

model = mujoco.MjModel.from_xml_path("m_pendulum.xml")
renderer = mujoco.Renderer(model, 640, 480)
data = mujoco.MjData(model)
mujoco.mj_forward(model, data)

# 初期化
n_frames, fps = 180, 60
frames = []
mujoco.mj_resetData(model, data)

# レンダリング
for i in range(n_frames):
    while data.time < i/fps:
        mujoco.mj_step(model, data)

    # 1秒経過時点で"hmotor"に-100の制御入力を与える
    if i == fps:
        data.ctrl[0] = -100

    renderer.update_scene(data, "fixed")
    frames.append(renderer.render())

save_video(frames, "output.mp4", fps)

属性 : actuator (MJCF)

　<actuator>はグルーピング要素であり、具象は<motor>や<position>などの子要素で定義します。以下にすべてのアクチュエータ要素で指定可能な属性のうち代表的なものを示します。すべての属性については「全アクチュエータ共通の属性の一覧」を参照してください。

以下に示す属性はすべてのアクチュエータショートカットに共通する属性であると同時に、<general>アクチュエータでも指定可能な属性です。上述のようにMuJoCoには内部的に<general>以外のアクチュエータ型は存在せず、ショートカットの独自の属性(例:<position>のkp属性)はすべてこれらの共通属性に変換されます。

表 代表的な全アクチュエータ共通の属性（<general>の属性）

属性	型:〈デフォルト値等〉 説明
name	型：string〈 optional 〉 名前です。
class	型：string〈 optional 〉 適用したい<default>の名前です。
ctrllimited	型：選択式〈 "auto" 〉 ["false","true","auto"]から選択 アクチュエータへの制御入力をクランプするか指定します。 "true" - 制御入力は実行時自動的にctrlrangeにクランプされます。 "false" - 制御入力はクランプされません。 "auto" - <compiler>のautolimitsが有効かつctrlrangeが定義されている場合にクランプされます。 制御入力のクランプはoption/flagのclampctrl属性からグローバルに無効化することも可能です。
forcelimited	型：選択式〈 "auto" 〉 ["false","true","auto"]から選択 アクチュエータの出力トルク/力をクランプするか指定します。 "true" - 制御入力は実行時自動的にforcerangeにクランプされます。 "false" - 制御入力はクランプされません。 "auto" - <compiler>のautolimitsが有効かつforcerangeが定義されている場合にクランプされます。
ctrlrange	型：real(2)〈 "0 0" 〉 制御入力をクランプする範囲を指定します。 １番目の値が最小値、２番目の値が最大値です。
forcerange	型：real(2)〈 "0 0" 〉 出力トルク/力をクランプする範囲を指定します。 １番目の値が最小値、２番目の値が最大値です。
gear	型：real(6)〈 "1 0 0 0 0 0" 〉 　アクチュエータの長さ $l_i$ をスケールします（このベクトルの長さ $|\pmb{gear}|$ がゲインとなる）。 　また、アクチュエータの接続対象の自由度が $1$ より大きいものについては、その出力の方向/軸を指定する役割も持ちます。多くの場合は第一要素だけが使用されますが、この場合のみ第二要素以降が使用されます。 　値の意味と直接影響する対象についてはトランスミッション節を、最終的に出力トルク/力にどのように影響するかについてはまとめ節を参照してください。
joint jointparent site refsite body tendon cranksite slidersite	型：string〈 optional 〉 アクチュエータを接続するオブジェクトを指定します。選択された属性によりトランスミッションのタイプが決定されます。この８属性のうち１つ（種類によっては２つ）を設定する必要があります。詳細は後述します。 ・joint - jointトランスミッションを構築します。大体のアクチュエータで指定可能です。 ・jointparent - jointとほとんど同じです。 ・site(&refsite) - siteトランスミッションを構築します。<position>などで指定可能です。 ・body - bodyトランスミッションを構築します。<adhesion>などで指定可能です。 ・tendon - tendonトランスミッションを構築します。<muscle>などで指定可能です。 ・cranksite&slidersite - slider-crankトランスミッションを構築します。両方の指定が必要であり、<position>などで指定可能です。

【全アクチュエータ共通の属性の一覧（generalの属性）】

属性	型:〈デフォルト値等〉 説明
name	型：string〈 optional 〉 名前です。
class	型：string〈 optional 〉 適用したい<default>の名前です。
group	型：int〈 "0" 〉 属するグループを指定します。カスタムタグおよび可視化時に使用できます。
ctrllimited	型：選択式〈 "auto" 〉 ["false","true","auto"]から選択 アクチュエータへの制御入力をクランプするか指定します。 "true" - 制御入力は実行時自動的にctrlrangeにクランプされます。 "false" - 制御入力はクランプされません。 "auto" - <compiler>のautolimitsが有効かつctrlrangeが定義されている場合にクランプされます。 制御入力のクランプはoption/flagのclampctrl属性からグローバルに無効化することも可能です。
forcelimited	型：選択式〈 "auto" 〉 ["false","true","auto"]から選択 アクチュエータの出力トルク/力をクランプするか指定します。 "true" - 制御入力は実行時自動的にforcerangeにクランプされます。 "false" - 制御入力はクランプされません。 "auto" - <compiler>のautolimitsが有効かつforcerangeが定義されている場合にクランプされます。
actlimited	型：選択式〈 "auto" 〉 ["false","true","auto"]から選択 アクチュエータに関連する内部状態（activation; 活性化状態）をクランプするか指定します。 "true" - 制御入力は実行時自動的にactrangeにクランプされます。 "false" - 制御入力はクランプされません。 "auto" - <compiler>のautolimitsが有効かつactrangeが定義されている場合にクランプされます。
ctrlrange	型：real(2)〈 "0 0" 〉 制御入力をクランプする範囲を指定します。 １番目の値が最小値、２番目の値が最大値です。
forcerange	型：real(2)〈 "0 0" 〉 出力トルク/力をクランプする範囲を指定します。 １番目の値が最小値、２番目の値が最大値です。
actrange	型：real(2)〈 "0 0" 〉 内部状態（activiation; 活性化状態）をクランプする範囲を指定します。 １番目の値が最小値、２番目の値が最大値です。詳細は活性化クランピングを参照してください。
lengthrange	型：real(2)〈 "0 0" 〉 アクチュエータのトランスミッションの実現可能な範囲を指定します。既定では<muscle>についてのみ適用されます（正確にはgaintypeorbiastypeが"muscle"のもの、<compiler>→<lengthrange>のmode属性から変更可能）。後述します。
gear	型：real(6)〈 "1 0 0 0 0 0" 〉 　アクチュエータの長さ $l_i$ をスケールします（このベクトルの長さ $|\pmb{gear}|$ がゲインとなる）。 　また、アクチュエータの接続対象の自由度が $1$ より大きいものについては、その出力の方向/軸を指定する役割も持ちます。多くの場合は第一要素だけが使用されますが、この場合のみ第二要素以降が使用されます。 　値の意味と直接影響する対象についてはトランスミッション節を、最終的に出力トルク/力にどのように影響するかについてはまとめ節を参照してください。
cranklength	型：real〈 "0" 〉 コネクティングロッド（コンロッド）の長さを指定します。 slider-crankトランスミッションの場合にのみ使用し、値は正である必要があります。
joint jointparent site refsite body tendon cranksite slidersite	型：string〈 optional 〉 アクチュエータを接続するオブジェクトを指定します。選択された属性によりトランスミッションのタイプが決定されます。この８属性のうち１つ（種類によっては２つ）を設定する必要があります。詳細は後述します。 ・joint - jointトランスミッションを構築します。大体のアクチュエータで指定可能です。 ・jointparent - jointとほとんど同じです。 ・site(&refsite) - siteトランスミッションを構築します。<position>などで指定可能です。 ・body - bodyトランスミッションを構築します。<adhesion>などで指定可能です。 ・tendon - tendonトランスミッションを構築します。<muscle>などで指定可能です。 ・cranksite&slidersite - slider-crankトランスミッションを構築します。両方の指定が必要であり、<position>などで指定可能です。
user	型：real(n)〈 "0 0 ..." 〉 nuser_actuatorと同じ要素数 詳細はユーザーパラメタを参照してください。
actdim	型：real〈 "-1" 〉 活性化状態の次元です。 "-1" - dyntypeに従い次元を設定します 1より大きい値 - ユーザ定義の活性化ダイナミクスのみで設定可能です。
dyntype	型：選択式〈 "none" 〉 ["none","integrator","filter","filterexact","muscle","user"]から選択 アクチュエータの活性化ダイナミクスを指定します。"none"の場合、アクチュエータは活性化状態を持ちません。 詳細は後述します。
gaintype	型：選択式〈 "fixed" 〉 ["fixed","affine","muscle","user"]から選択 　力生成メカニズムの出力（のゲイン(係数)）を決定します。MuJoCoのアクチュエータモデルでは次のように出力トルク/力が決定されます。ここで $w_i,u_i$ はそれぞれ活性化状態と制御入力です。また、 $Gain, Bias$ はそれぞれゲイン(係数)とバイアス項ですが、実際の値はgaintype/biastypeにより変化します。詳細は後述します。 　　 $F_i = Gain\times (w_i \space or\space u_i) + Bias$
biastype	型：選択式〈 "none" 〉 ["none","affine","muscle","user"]から選択 力生成メカニズムの出力（のバイアス項）を決定します。詳細は後述します。
dynprm	型：real(10)〈 "1 0 ... 0" 〉 活性化ダイナミクスのパラメタです。組み込みのアクチュエータショートカットの場合、筋肉を除き１番目の値のみ使用します。"muscle"の場合は３つ目までの値が使われます。
gainprm	型：real(10)〈 "1 0 ... 0" 〉 ゲインのパラメタです。組み込みのアクチュエータショートカットの場合、筋肉を除き１番目の値のみ使用します。"muscle"の場合は９つめまでの値が使われます。
biasprm	型：real(10)〈 "1 0 ... 0" 〉 バイアス項のパラメタです。バイアス型が"affine"の場合は３つめまでの値を使用します。"none"の場合値は使用されず（ $Bias=0$ ）、"muscle"の場合は９つ目まで使用されます。
actearly	型：選択式〈 "false" 〉 ["false","true"]から選択 "true"を指定すると、力の計算は現在の値ではなく次の活性化変数の値を使用するようになります。このフラグを設定すると、制御と加速の間の遅延が1タイムステップ短くなります。

各アクチュエータショートカットにおいてactdim～biasprmの７属性は自動的に設定されます。したがって、通常はこれ以外の属性＆ショートカット固有の属性のみを指定することになります。

actuator詳説 : アクチュエータショートカット

各ショートカットごとの指定する（べき）属性

　アクチュエータの種類節で述べたように、MuJoCoには<general>要素のほかに、特定の用途に特化したアクチュエータショートカットが用意されています。各ショートカットには固有の性質があり、初期値の設定が異なります。このため、後述するトランスミッションとの組み合わせにより、設定が必要な属性が変わってきます。

　以下に、代表的なショートカットについて、どの属性を設定する必要があるか(設定する意味があるか)を示します。記載していない組み合わせ（例: <motor>と<tendon>）も可能ですが、おおよそ適用範囲は類似のものになると思われます。基本的には「❕」と「〇」、固有の属性（kp等）のみを設定すればよいと思います。各記号の意味は以下の通りです。

• ❕ : 必須
• 〇 : 設定可能（設定することに意味がある）
• trueなど : デフォルトで値が設定されている（変更すべきではない）
• △ : 設定可能だが固有属性を使用するべき（値を変更すべきではない）
  • ショートカット固有の属性を参照する属性です
  • (例) <position>のgainprm属性はkp属性を参照し、値を自動で設定します

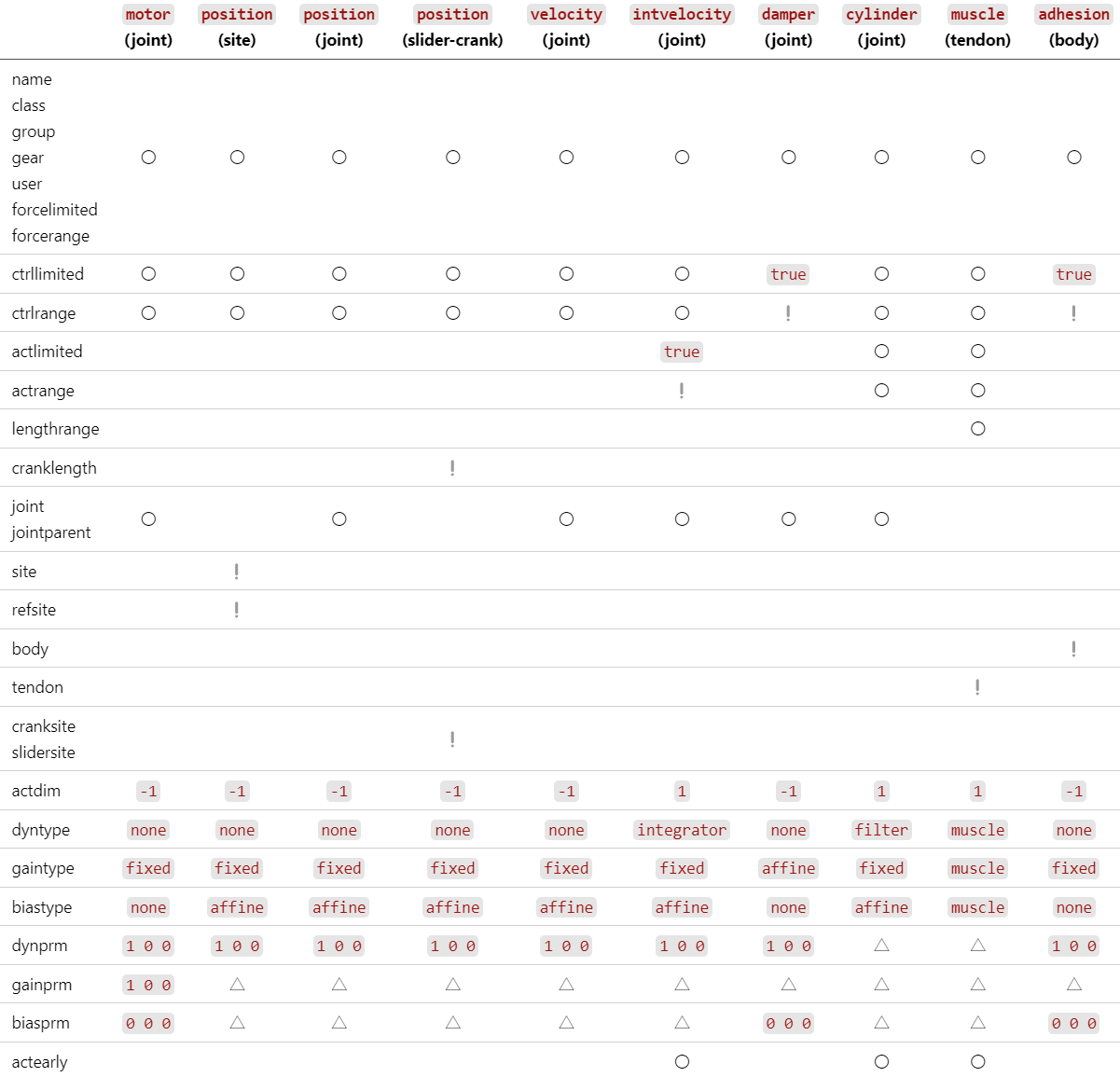
表 各ショートカットと各属性の適用可否．<general>アクチュエータについてはすべての属性を設定可能です．

【表をテキスト形式で見る】

	motor (joint)	position (site)	position (joint)	position (slider-crank)	velocity (joint)	intvelocity (joint)	damper (joint)	cylinder (joint)	muscle (tendon)	adhesion (body)
name class group gear user forcelimited forcerange	〇	〇	〇	〇	〇	〇	〇	〇	〇	〇
ctrllimited	〇	〇	〇	〇	〇	〇	true	〇	〇	true
ctrlrange	〇	〇	〇	〇	〇	〇	❕	〇	〇	❕
actlimited						true		〇	〇
actrange						❕		〇	〇
lengthrange									〇
cranklength				❕
joint jointparent	〇		〇		〇	〇	〇	〇
site		❕
refsite		❕
body										❕
tendon									❕
cranksite slidersite				❕
actdim	-1	-1	-1	-1	-1	1	-1	1	1	-1
dyntype	none	none	none	none	none	integrator	none	filter	muscle	none
gaintype	fixed	fixed	fixed	fixed	fixed	fixed	affine	fixed	muscle	fixed
biastype	none	affine	affine	affine	affine	affine	none	affine	muscle	none
dynprm	1 0 0	1 0 0	1 0 0	1 0 0	1 0 0	1 0 0	1 0 0	△	△	1 0 0
gainprm	1 0 0	△	△	△	△	△	△	△	△	△
biasprm	0 0 0	△	△	△	△	△	0 0 0	△	△	0 0 0
actearly						〇		〇	〇

<position>(slider-crank)：slider-crankトランスミッションによるアクチュエータです。これのみ接続対象をcranksiteとslidersiteの２つ設定する必要があります。

<position>(site)：若干特殊でrefsite属性の指定が必須です。本来siteトランスミッションはrefsite属性の指定を必要とはしないのですが、refsiteを指定しない場合にはアクチュエータ長 $l_i=0$ となるため<position>では使用できません。

【上表の参考文献（モデル/プログラム）】

　上記内容のうち、actdim属性より上の属性についてはMuJoCoのGitHubから具体例を調べて記述を行っています。以下は各ショートカットと適用対象の例です（括弧付きのものはplugin関連）。

• <motor>
  • joint:car.xml, tendon:car.xml, model.xml, (site:cable.xmlなど)
• <position>
  • hinge-joint:binding_test.py, slide-joint:active_adhesion.xml, slider-crank:slider_crank.xml, (site:smooth_test.py)
• <velocity>
  • hinge-joint:robot_arm.xml
• <intvelocity>
  • hinge-joint:model.xml
• <damper>
  • hinge-joint:damper.xml
• <cylinder>
  • hinge-joint:MjActuatorTests.cs
• <muscle>
  • tendon:arm26.xml, activation.xml, hinge-joint:xml_native_reader_test.cc
• <adhesion>
  • body:active_adhesion.xml

各アクチュエータの詳細

　ここから7節にわたり、<muscle>と<plugin>を除いた各アクチュエータの詳細を説明します。ここで、以下に説明する力生成メカニズムについて簡単な説明を行います。この詳細については力生成メカニズム節および活性化ダイナミクス節を参照してください。

本節では<muscle>と<plugin>についての説明は行いません。<plugin>に関してはengine pluginによりその詳細が変わるためで、詳細はXML Reference/actuator/pluginを参照してください。また<muslce>についてはその概要が非常に複雑かつ冗長となるため、本ページの末尾で説明を行います。

motor (MJCF/actuator)

　<motor>は制御入力 $u_i$ と出力トルク/力 $p_i$ が一致する（ $p_i = u_i$ ）、最もシンプルなアクチュエータ要素です。アクチュエータがよくわからない場合はとりあえずこれを試してみるとよいと思います。

　<motor>には固有の属性は存在しません。また、gainprm等のパラメタは以下のように設定されます。

種類	タイプ	値
活性化	なし	dyntype="none"、dynprm= $(1,0,0)$
ゲイン	"fixed"	gaintype="fixed"、gainprm= $(1,0,0)$
バイアス	なし	biastype="none"、biasprm= $(0,0,0)$

position (MJCF/actuator)

　<position>はポジションサーボであり、現在位置と目標位置の差に基づいてトルクを連続的に調整し、ジョイントを所望の位置へ駆動させます。物体の把持などの位置決め制御に用いられます。

　また、slider-crankトランスミッション（簡易なスライダークランク機構）を使用する場合は一般にこのショートカットを使用します。<position>を利用したスライダークランク機構の具体例はslider-crankトランスミッション節を参照してください。

図 固有の属性（<position>）

属性	型:〈デフォルト値等〉 説明
kp	型：real〈 "1" 〉 位置のフィードバックゲインです。
kv	型：real〈 "0" 〉 アクチュエータの減衰です。 ※減衰を有効にする場合、<option>のintegrator属性を"implicit"か"implicitfast"にすることをお勧めします。
inheritrange	型：real〈 "0" 〉 $0$ 以外の値に設定した場合、アクチュエータの接続対象に合わせてctrlrangeを自動設定します。詳細は後述します。

　<position>では、gainprm等のパラメタは以下のように設定されます。

種類	タイプ	値
活性化	なし	dyntype="none"、dynprm= $(1,0,0)$
ゲイン	"fixed"	gaintype="fixed"、gainprm= $(k_p,0,0)$
バイアス	"affine"	biastype="affine"、biasprm= $(0,-k_p,-k_v)$

inheritrangeについて

　inheritrangeは<position>と<intvelocity>で指定可能な属性です。この値が $0$ 以外の正値に設定された場合、アクチュエータの接続対象の可動範囲を利用してctrlrangeを自動で設定します。

　正の値 $r$ に設定したとき、ctrlrangeは $r$ でスケールされた対象の範囲の中点付近に設定されます。例えば接続対象の範囲が $[0,1]$ のときの、種々の $r$ に対するctrlrangeの設定値を以下に示します。

• $r=0.8$ ： ctrlrange ＝ $[0.1,0.9]$
• $r=1.0$ ： ctrlrange ＝ $[0.0,1.0]$
• $r=1.2$ ： ctrlrange ＝ $[-0.1, 1.1]$

上記の例からわかるように、 $1$ より小さい値は、制限に達しないようにするのに役立ちます。また $1$ より大きい値は、制御権限を限界に維持する (限界を押し上げることができる) のに役立ちます。

velocity (MJCF/actuator)

　<velocity>は速度サーボであり、所望の関節速度を達成するように、現在のジョイント速度と目標速度の差に合わせてトルクを連続的に調整します。ホイールの回転制御など、関節速度の維持が重要なケースに使用します。

図 固有の属性（<velocity>）

属性	型:〈デフォルト値等〉 説明
kv	型：real〈 "1" 〉 位置のフィードバックゲインです。

　<velocity>では、gainprm等のパラメタは以下のように設定されます。

種類	タイプ	値
活性化	なし	dyntype="none"、dynprm= $(1,0,0)$
ゲイン	"fixed"	gaintype="fixed"、gainprm= $(k_v,0,0)$
バイアス	"affine"	biastype="affine"、biasprm= $(0,0,-k_v)$

intvelocity (MJCF/actuator)

　<intvelocity>は積分速度サーボです。<velocity>が速度に直接フィードバックを返すのに対し、<intvelocity>は積分器と位置フィードバックを統合しています。このため、活性化状態 $w_i$ は「ポジションアクチュエータ」の設定値、制御入力 $u_i$ は「ポジションアクチュエータの設定値の速度」を意味します。実際のロボットシステムでは、速度情報を持つアクチュエータの最も一般的な実装が<intvelocity>となります。

図 固有の属性（<intvelocity>）

属性	型:〈デフォルト値等〉 説明
kp	型：real〈 "1" 〉 位置のフィードバックゲインです。
kv	型：real〈 "0" 〉 アクチュエータの減衰です。 ※減衰を有効にする場合、<option>のintegrator属性を"implicit"か"implicitfast"にすることをお勧めします。
inheritrange	型：real〈 "0" 〉 $0$ 以外の値に設定した場合、アクチュエータの接続対象に合わせてctrlrangeを自動設定します。詳細は前述したとおりです。

　<intvelocity>では、gainprm等のパラメタは以下のように設定されます。したがって、"actrange"を指定する必要があります。仮に設定しない場合、ターゲットである位置がジョイントの限界を超えて積分され続け、制御性が失われます。また、actrangeの単位は $\mathrm{rad}$ です。

種類	タイプ	値
活性化	なし	dyntype="none"、dynprm= $(1,0,0)$
ゲイン	"fixed"	gaintype="fixed"、gainprm= $(k_p,0,0)$
バイアス	"affine"	biastype="affine"、biasprm= $(0,-k_p,-k_v)$
その他		actlimited="true"

damper (MJCF/actuator)

　<damper>はアクティブダンパーであり、出力 $p_i$ が速度 $v_i$ と制御入力 $u_i>0$ に負比例（ $p_i=-k_v\times v_i\times u_i$ ）します。 $k_v>0$ は速度フィードバックゲインです。使用時はoptionのintegrator属性をimplicitまたはimplicitfastにすることが推奨されます。使用例がsiteトランスミッション節にあります。

図 固有の属性（<damper>）

属性	型:〈デフォルト値等〉 説明
kv	型：real〈 "1" 〉 速度のフィードバックゲインです。

　<damper>では、gainprm等のパラメタは以下のように設定されます。したがって、"ctrlrange"を指定する必要があります。

種類	タイプ	値
活性化	なし	dyntype="none"、dynprm= $(1,0,0)$
ゲイン	"affine"	gaintype="affine"、gainprm= $(0,0,-k_v)$
バイアス	なし	biastype="none"、biasprm= $(0,0,0)$
その他		ctrllimited="true"

cylinder (MJCF/actuator)

　<cylinder>は空気圧シリンダまたは油圧シリンダをモデリングするのに使用します。

図 固有の属性（<cylinder>）

属性	型:〈デフォルト値等〉 説明
timeconst	型：real〈 "1" 〉 活性化ダイナミクスの時定数 $\tau$ です。
area	型：real〈 "1" 〉 シリンダの面積 $A$ です。アクチュエータのゲインに影響します。
diameter	型：real〈 optional 〉 シリンダの直径です。この値が指定された場合、areaを $A=\pi d^2/4$ として上書きします。
bias	型：real(3)〈 "0 0 0" 〉 バイアスのパラメタです。

　<cylinder>では、gainprm等のパラメタは以下のように設定されます。ここで $b_i$ $(i=0,1,2)$ はbias属性の値です。

種類	タイプ	値
活性化	"filter"	dyntype="filter"、dynprm= $(\tau,0,0)$
ゲイン	"fixed"	gaintype="fixed"、gainprm= $(A,0,0)$
バイアス	"affine"	biastype="affine"、biasprm= $(b_0,b_1,b_2)$

情報が全然ない…

adhesion (MJCF/actuator)

　<adhesion>は吸着力を発生させるアクチュエータです。ヤモリの足や吸盤などをシミュレートできます。吸着力は接触面積に比例せず、各接触点に出力 $p_i$ が等分配されます。これは、後述するようにMuJoCoに面接触が存在しないためです。使用例はリンク先を参照してください。

図 固有の属性（<adhesion>）

属性	型:〈デフォルト値等〉 説明
body	型：string〈 required 〉 吸着力を発生させるボディです。
gain	型：real〈 "1" 〉 アクチュエータのゲインです。接触力の総和 $p_i$ はこの値と制御入力 $u_i$ の積となり（ $p_i=gain_0\times u_i$ ）、各接触点にこの力が等分配されます（接触点数 $n$ のとき、各点の接触力 $p_{i,j} = p_i/n$）。

　<adhesion>では、gainprm等のパラメタは以下のように設定されます。したがって、"ctrlrange"を指定する必要があります。

種類	タイプ	値
活性化	なし	dyntype="none"、dynprm= $(1,0,0)$
ゲイン	"fixed"	gaintype="fixed"、gainprm= $(gain_0,0,0)$
バイアス	なし	biastype="none"、biasprm= $(0,0,0)$
その他		trntype="body" ctrllimited="true"

重要なパラメタ等

gear

　gear属性はアクチュエータ長/速度 $l_i/\dot{l_i}$ をスケーリングする役割を持つ値です。この値 $\pmb{gear}\in\mathbb{R}^6$ を用いて、 $l_i,\dot{l_i}$ が $|\pmb{gear}|$ 倍されます。これが出力にどう影響するかについてはアクチュエータモデルのまとめ節を参照してください。雑に言うと、各アクチュエータがターゲットとする量（<velocity>なら速度/角速度 $v/\omega$ ）に対する敏感さ(?)を指定します。

　また、ボールジョイントを接続対象とするものや<site>を接続対象とするものなど、接続対象の自由度が $1$ よりも大きいアクチュエータについては、gear属性がその出力の方向/軸を決定します。gear属性の第２要素以降が指定されるのはこのときだけで、第３要素までか第６要素までを指定します。jointトランスミッション節やsiteトランスミッション節にその具体例などが記載されています。基本的には以下の通りですが（ $(x,y,z,r_x,r_y,r_z) := \pmb{gear}$ ）、ボールジョイントに接続した場合には最初の３要素が回転軸を定義します。

• $r_x,r_y,r_z=0$ のとき
  • $(x,y,z)$ は力を与える方向を示すベクトル
  • ３要素（例: "0 .7 .7"）や６要素（例: "0 .7 .7 0 0 0"）で指定
• $x,y,z=0$ のとき
  • $(r_x,r_y,r_z)$ はトルクを与える軸
  • ６要素（例: "0 0 0 1 0 0"）

lengthrange

　lengthrange属性は、アクチュエータの伸び縮みの範囲を制限します。この範囲は、トランスミッション機構によって規定されるアクチュエータ長 $l_i$ の最小値と最大値で表されます。デフォルトでは<muscle>アクチュエータでのみ有効になっていますが、<compiler>の<lengthrange>要素のmode属性で変更可能です。この範囲について、以下では単にlengthrangeと呼びます。

mjModel上のすべての物理量・幾何量は正確な値ですが、この属性の値（mjModel.actuator_length）のみ近似値となることに注意が必要です。

　すべてのアクチュエータのうち、<muscle>アクチュエータについては、lengthrangeを明示的に指定する必要があります。ただし、その方法は以下の3通りあります。

1. lengthrange属性から直接指定する
2. アクチュエータの接続対象（ジョイントor腱）の可動範囲がコピーされる
3. モデルをコンパイルする際に自動計算される

【lengthrangeの自動計算】

　lengthrangeの自動計算はコンパイル時に行われます。この際、重力や摩擦、接触などを無視した状態で実際にアクチュエータを物理シミュレーションし、その可動範囲を最適化することで範囲を決定しています。この自動計算はある程度の時間を必要としますが、これはシミュレーションによる最適化を利用して範囲の値を決めているためです。詳細はComputation/Length rangeを参照してください。

特に大規模な骨格筋モデルの場合、自動計算はかなりの時間を必要とします。MuJoCoコンパイラはこのためにマルチスレッド化されており、各アクチュエータが平行して処理されることで高速にコンパイルすることが可能です（このため、LinuxおよびmacOSではユーザーコードをリンクする際に-pthreadフラグが必要となります）。それでも処理には時間がかかるため、読み込んだモデルはXML/MJBファイルとして保存することをお勧めします。

　シミュレーションに際しては、実現可能なアクチュエータの長さがモデル上で実際に制限されていることが要求されます。そうでない場合はコンパイラがエラーを返します。すなわち、アクチュエータはモデル内で定義されたジョイントや腱の制限、または幾何学的構造により制限される必要があります。後者の例を下図に示します。このとき、<tendon>の最小・最大長さは接続点が描く円の大きさによって決まります。ただし、<joint>や<tendon>に制限がない場合、アクチュエータ長は無制限になり得ます。

図 幾何学的構造によるlengthrangeの制限．わかりやすさのため、ヒンジジョイントにはトルクを加えている

　自動計算でlengthrangeが求められなかった場合、コンパイラはエラーを返します。実際には<spatial>に付いた<muscle>アクチュエータでlengthrangeが使われることが多いため、エラーの原因はジョイントに可動範囲を設定し忘れたことである可能性が高いです。

力の制限

　通常、アクチュエータの力には上限と下限が存在します。この制限は以下の方法で規定することができます。各オプションは排他的ではないので、必要に応じて組み合わせることも可能です。

属性	説明
ctrlrange	制御入力をクランプします。 単純なモーターであれば、これは出力を制御することに同じです。
forcerange	アクチュエータ出力トルク/力をクランプします。 例えば<position>の力を範囲内に保つ際などに便利です。ただし、通常はジョイントの可動範囲を超えないように制御範囲もクランプする必要があります。
actuatorfrcrange (<joint>)	（アクチュエータではなく）ジョイント側で出力をクランプします。 トランスミッションを経由してジョイントに作用するすべてのアクチュエータからの入力を制御します。複数のアクチュエータが単一のジョイントに作用する際に便利です。以下に例を示します。

actuator詳説 : アクチュエータモデル

　MuJoCoでは様々なアクチュエータモデルを使用できます。すべてのアクチュエータは単一入力単一出力であり、制御入力 $u_i$ に対して力/トルクの出力 $p_i$ が決定されます。このとき、入出力 $u_i,p_i$ はいずれもスカラー値です。また、一部のアクチュエータ（<intvelocity>、<cylinder>、<muscle>）は活性化状態 (activations) $w_i$ という内部状態を持ちます。

アクチュエータ出力の算出手順

　アクチュエータの動作を決定する3つの要素を以下に示します。これらは個別に設定可能なため、MuJoCoのアクチュエータ(特に<general>)は非常に柔軟性が高くなっています。一方で、アクチュエータショートカットを使うと、特定の機能を持つアクチュエータを簡単に作れます。ショートカットは設定できるパラメタが少なく柔軟性は低めですが、通常はこちらを使うことになるでしょう。

表 アクチュエータの動作を決定する３要素

構成要素	説明
トランスミッション	力を何に、どのような形で出力するかを決定します。接続対象の自由度が $2$ 以上の場合はその出力軸も決定します。また、gear属性はこの段階でアクチュエータ長/速度 $l_i/\dot{l_i}$ をスケーリングします。
活性化ダイナミクス	制御入力 $u_i$ を一定の規則のもとで加工し、活性化状態 $w_i$ を生成します。 　内部状態を持つアクチュエータ（<intvelocity>, <cylinder>, <muscle>）で有効で、システムの複雑さを増すために使用されます（出力が現在の値だけでなく、過去の履歴にも依存するようになります）。
力の生成 (force generation)	以下の基本式に従い、出力するトルク/力 $p_i$ を決定します。ここで、 $Gain,Bias$ は後述するゲインとバイアス項です。内部状態があれば $w_i$ を、なければ $u_i$ を使います。 　　 $p_i = Gain\times(u_i\space or\space w_i) + Bias$

上記の３要素はそれぞれ順を追って計算されます。したがって、アクチュエータが出力トルク/力を得るまでには、以下の２または３段階を経ることになります。

1. 出力 $p_i$ の伝達特性（出力の軸/方向）を決定、同時に $l_i,\dot{l_i}$ を計算
2. （活性化状態 $w_i$ の計算）
3. $w_i\space or \space u_i$ を用いて出力トルク/力 $p_i$ を計算

actuator詳説 : トランスミッション

概要：トランスミッション

　トランスミッションはアクチュエータの力の伝達特性のことであり、アクチュエータの接続対象によって決定されます。トランスミッションのタイプにより、どのような力が働くのか、制御入力に対してどのように力が計算されるかなどが変化します。

　各アクチュエータはスカラー長 $l_i(q)$ を持ちます。この値はトランスミッションの種類とそのパラメータによって定義されます。またその勾配 $\nabla l_i =: N_i\in\mathbb{R}^n_v$ はモーメントアームのベクトルであり、スカラーのアクチュエータ力から関節力へのマッピングを決定します。この際の伝達特性を規定するのが、以下に示すトランスミッションのタイプということになります。

雑に言えば、 $l_i$ と $\dot{l_i}(=N_i\cdot\pmb{q}_\mathrm{vel})$ は（入力 $u_i$ と併せて）出力の大きさを決定する役割を、勾配 $N_i = \nabla l_i$ は出力の方向/軸を決定する役割を持つといえます。

　トランスミッションには６つのタイプがあります。タイプはおおよそ取り付け先のオブジェクトにより決定され、それぞれについて指定する必要のある属性が変化します。ここでは、lengthrangeからslidersiteまでの10属性について、各タイプで指定する（べき）ものと、使用可能なアクチュエータショートカットがどれであるかを示します。

「使用可能な」とか「指定すべき」とか書いてますが、以下で示していない組合せを使用することができないわけではないです。あくまでGitHubのコード例を参考に考えた使いやすい組合せです。また、当然ながら<general>はすべてのトランスミッションタイプを指定可能です。

タイプ	使用可能な ショートカット	指定する属性: 説明
joint	<motor> <position> <velocity> <intvelocity> <damper> <muscle>	指定属性: joint 　対象のジョイントに力またはトルクを加えるアクチュエータを作成します。 　"hinge"や"slide"ジョイントの場合、および腱の場合はシンプルにトルク/力を加えるアクチュエータとなります。詳細は後述します。 ※ lengthrange属性は<muscle>アクチュエータを使用する場合にのみ指定します（既定）。
tendon	同上	指定属性: (lengthrange), tendon 対象の腱に力を加えるアクチュエータを作成します。詳細は後述します。
jointparent	<motor> <position> <velocity> <intvelocity> <damper>	指定属性: jointparent 　対象のジョイントに力またはトルクを加えるアクチュエータを作成します。 "slide"/"hinge" - joint属性と全く同じ挙動を示します "ball"/"free" - gear属性で指定する回転軸が親の座標系で定義されます（joint属性の場合は子のローカル座標系で回転軸が定義される）。jointトランスミッション節も参照してください。
slider-crank	<position>	指定属性: cranklength,cranksite,slidersite 　ピストン駆動内燃機関のように、直線力をトルクに変換するアクチュエータを作成します。詳細は後述します。 💡<equality>を使用して明示的にモデル化することも可能ですが、低効率で安定性に劣ります。
body	<adhesion>	指定属性:body 　ボディとの接触点に接触法線方向の線形力を加えることのできるアクチュエータを作成します。簡単にいうとヤモリの足や吸盤、磁石のような「吸着する物体」をシミュレートできます。 bodyトランスミッションの長さは $l_i(q)=0$ です。詳細は後述します。
site	<motor> <position> <velocity> <intvelocity> <damper>	指定属性: site,refsite 　<site>に（<site>座標系に従った）力/トルクを加えることができるアクチュエータを作成します。ジェットやプロペラをモデル化するのに役立ちます。 　refsite属性も併せて指定されている場合、refsiteの座標系に従い力/トルクが与えられます。 既定でsiteトランスミッションのアクチュエータ長は $l_i(q)=0$ です（refsite属性を指定した場合を除く）。詳細は後述します。

スカラー長 $l_i(q)=0$ であるもの（body/siteトランスミッション）については、<position>アクチュエータに使用することはできません。すなわち、body属性とsite属性を指定することはできません。

トランスミッションタイプとアクチュエータ長/速度

　以下にトランスミッションのタイプごとのアクチュエータ長/速度の計算式を示します。以下からわかるように、gear属性はアクチュエータ長/速度と、その参照値との間のゲインを決定する役割を持ちます（＋出力の方向/軸を決定する役割を持つ）。

表 トランスミッションのタイプ（伝達方式）とアクチュエータ長さ $l_i$ および同速度 $\dot{l_i}$ ．要素数はgear属性で指定する要素の数

伝達方式	下位分類	要素数	式
joint / jointparent	"hinge"	1	gear属性は関節角度/角速度 $\theta / \omega$ の増幅率 $gear_0$ を指定します。本項目については、jointparentトランスミッションであっても挙動は変化しません。以下の"slide"についても同様です。 　　 $l_i = gear_0 \times \theta$ 　　 $\dot{l_i} = gear_0 \times \omega$
〃	"slide"	1	$x/v$ はそれぞれ関節変位/速度です。 　　 $l_i = gear_0 \times x$ 　　 $\dot{l_i} = gear_0 \times v$
〃	"ball" ※1	3	クォータニオン表現による回転角 $\theta$ と方向ベクトル $\pmb{n}=(x,y,z)$ 、gear属性 $\pmb{gear}\in\mathbb{R}^3$ 、および関節角速度 $(\omega_x,\omega_y,\omega_z)$ を用いて以下のように表せます。 　　 $l_i = (\pmb{n} \cdot \pmb{gear})\space \theta$ （ $where\space \theta\in[-\pi,\pi]$ ） 　　 $\dot{l_i} = |\pmb{gear}| \space \sqrt{\omega_x^2+\omega_y^2+\omega_z^2}$ 　ここで $\pmb{gear}$ は出力トルクを流す回転軸を意味します。jointトランスミッションの場合、この回転軸はローカル座標系で定義されます。一方、jointparentトランスミッションの場合は親のローカル座標系で定義されます。 　関節角速度 $(\omega_x,\omega_y,\omega_z)$ はmjData.qvel[n:n+3]で取得できるものに同じです。
〃	"free"	6	gear属性の値 $\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はワールド座標系での出力力を加える方向 $(x,y,z)$ と、ローカル座標系での出力トルクを加える回転軸 $(r_x,r_y,r_z)$ を指定します。また、jointparentトランスミッションの場合、回転軸はワールド座標系上で定義されます。 　ボディの速度 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ （mjData.qvel[n:n+6]の値）を用いて、以下のように表せます※2。 　　 $l_i=0$ 　　 $\dot{l_i} = \pmb{v}\cdot \pmb{gear}$
tendon	-	1	gear属性の値 $gear_0$ は、腱全体の長さ $l_{tendon}$ /腱長の変化率 $v_{tendon}$ に対する増幅率を指定します。<spatial>と<fixed>のどちらにも適用可能です。 　　 $l_i = gear_0\times l_{tendon}$ 　　 $\dot{l_i} = gear_0 \times v_{tendon}$
slider-crank	-	1	gear属性の値 $gear_0$ は、スライダーの位置 $z$ の増減率を指定します。<position>アクチュエータの場合は制御入力 $u_i \simeq z\space (t>>0)$ です。詳細は後述します。 　　 $l_i = gear_0 \times z$ 　　 $\dot{l_i} = gear_0\left(\frac{\partial l_i}{\partial\pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega$ ここで、slidersiteの $z$ 軸ベクトルを $\pmb{a}\in\mathbb{R}^3$ 、slidersiteからcranksiteまでのベクトルを $\pmb{v}_\mathrm{rod}\in\mathbb{R}^3$ 、cranklengthを $r$ としました。また、 $\theta,\omega$ はcranksiteを取り付けたボディのヒンジジョイントの角度/角速度です。詳細は後述します。
body	-	0	gear属性の指定はできません。また、通常<adhesion>アクチュエータに取り付けますが、この際に $\dot{l_i}$ は出力 $p_i$ に影響しません。 　　 $l_i=0$ 　また、このトランスミッションで出力 $p_i$ は、すべての接触点に等分配されます。すなわち、例えば接触点が４個の場合は各点に $p_i/4$ の力が働きます。
site	-	3 or 6	refsiteが指定されていない場合は次のようになります。ここで、 $\nabla l_i$ はアクチュエータのモーメント、 $\pmb{q}_\mathrm{vel}\in\mathbb{R}^{n_v}$ は各自由度ごとの速度です。詳細は後述します。 　　 $l_i=0$ 　　 $\dot{l_i} = \nabla l_i\cdot\pmb{q}_\mathrm{vel}$ 　refsiteが指定されている場合は次のようになります。ここで、siteとrefsiteの中心位置、クォータニオンをそれぞれ $\pmb{x}_\mathrm{site}, \pmb{x}_\mathrm{ref}$ 、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ とし、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ の差分を $\pmb{\omega}$ とします。詳細は後述します。 　　 $l_i = \pmb{gear}\cdot\pmb{\chi}\space\space \mathrm{where}\space\space \pmb{\chi} = \begin{bmatrix}\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}\\ \pmb{\omega}\end{bmatrix}$ 　　 $\dot{l_i} = \nabla l_i\cdot\pmb{q}_\mathrm{vel}$

※1 : クォータニオン表現による回転の表現は $(\cos\frac{\theta}{2}, x\sin\frac{\theta}{2}, y\sin\frac{\theta}{2}, z\sin\frac{\theta}{2})$ です（このとき方向ベクトル $(x,y,z)$ は単位ベクトル）。ボールジョイント回転角のクォータニオンはmjData.qpos[n:n+4]により取得可能です。回転角 $\theta$ の値は $[-\pi,\pi]$ の範囲にに制限され、回転角が $\pi$ を超えると $\pi$ に折り返され、その逆も同様に変化します。このように制限された $\theta$ の下で、アクチュエータの長さ $l_i$ は以下のように計算されます。

$$\begin{aligned}
l_i =& (\pmb{n}\cdot\pmb{gear})\theta\\
\Big( =& (x\space gear_0 + y\space gear_1 + z\space gear_2)\theta \Big) \end{aligned}$$

このため、ボールジョイントに接続したアクチュエータの長さは $-\pi|\pmb{gear}|\le l_i \le \pi |\pmb{gear}|$ に制限されます。

※2 : フリージョイントを指定するjointトランスミッションについて、アクチュエータの速度 $\dot{l_i}$ は、ボディの速度 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ とgear属性 $\pmb{gear}$ の内積 $\pmb{v}\cdot\pmb{gear}$ として記述しました。ただ、この式については若干確証が持てていないです（記述も恐らくなかった）。

　検証時は大体有効数字3桁以降で差異が出ていました（ $\dot{l_i}>\pmb{v}\cdot\pmb{gear}$ ）。いくつか他の種類についても検証を行いましたが、少なくとも $|\pmb{gear}||\pmb{v}|$ や $|\pmb{gear}||(v_x\space v_y\space v_z)|$ 、 $|\pmb{gear}||(\omega_x\space \omega_y\space \omega_z)|$ あたりではありませんでした。

トランスミッションの計算

　上ではトランスミッションの種類により $l_i$ と $\dot{l_i}$ の計算式が変化すると書きましたが、実際にはもう少し複雑な処理となっています。というのも $\dot{l_i}$ を計算する前段階としてアクチュエータのモーメント $N_i=\nabla l_i$ を計算するためで、こちらは他のアクチュエータ要素等にも影響を受けるため計算式が複雑になりやすいです。

　以下では、アクチュエータの接続対象の状態（ $x,v$ 、 $\theta,\omega$ など）と、アクチュエータの状態 $l_i,\dot{l_i}$ との関係が特に複雑なものについてその計算式を記述します。基本的にmj_transmissionを参照しています。

【トランスミッションの計算の詳細】

---

slider-crankトランスミッション

　①アクチュエータ長 $l_i$ : slidersiteの $z$ 軸ベクトルを $\pmb{a}\in\mathbb{R}^3$ 、slidersiteからcranksiteまでのベクトルを $\pmb{v}_\mathrm{rod}\in\mathbb{R}^3$ とします。また、cranklengthを $r$ とします。このとき、 $l_i$ は

$$\begin{aligned} l_i &= gear_0\times z\\z &= \pmb{a}\cdot\pmb{v}_\mathrm{rod} - \sqrt{det}\space\space\space\mathrm{where}\space det = (\pmb{a}\cdot\pmb{v}_\mathrm{rod})^2 + r^2 - |\pmb{v}_\mathrm{rod}|^2\end{aligned}$$

となります。ただし、ルート部分が虚数となった場合は $l_i = \pmb{a}\cdot\pmb{v}_\mathrm{rod}$ として計算されます。

　②アクチュエータのモーメント $N_i$ ： $l_i$ についての $\pmb{a},\pmb{v}_\mathrm{rod}$ による偏微分はそれぞれ

$$\frac{\partial l_i}{\partial \pmb{a}} = \pmb{v}_{rod}\left(1-\frac{\pmb{a}\cdot\pmb{v}_\mathrm{rod}}{\sqrt{det}} \right),\space\space\space \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}} = \pmb{a}\left(1-\frac{\pmb{a}\cdot\pmb{v}_\mathrm{rod}}{\sqrt{det}}\right)+\pmb{v}_\mathrm{rod}\left(\frac{1}{\sqrt{det}}\right)$$

と書けます。したがって、チェーンルールにより $N_i$ は以下のように計算されます。ここで、 $J_a,J_v$ はそれぞれ $\pmb{a},\pmb{v}_\mathrm{rod}$ のヤコビ行列（ $(3\times n_v)$ 行列）です。

$$N_i = gear_0\times\left(J_a^\mathsf{T}\frac{\partial l_i}{\partial \pmb{a}} + J_v^\mathsf{T}\frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}} \right)$$

　③アクチュエータ速度 $\dot{l_i}$ ：各自由度ごとの速度 $\pmb{q}_\mathrm{vel}\in\mathbb{R}^{n_v}$ を用いて、以下の式で計算されます。

$$\dot{l_i} = N_i\cdot\pmb{q}_\mathrm{vel}$$

　さて、以下に示すような、ヒンジジョイントのみを備えたモデルを用いて $l_i$ について考えてみましょう。すなわち、他のアクチュエータ等の影響を受けないと仮定します。このとき、ジョイントの角度、角速度をそれぞれ $\theta$ 、 $\omega$ とします。このときヤコビ行列 $J_a,J_v$ はそれぞれ

$$J_a = \frac{\partial \pmb{a}}{\partial \theta},\space\space\space J_v = \frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}$$

と表されます。これを上の式に代入してわかりやすい形に整理すると、アクチュエータ速度 $\dot{l_i}$ は以下のように表されます。

$$\dot{l_i} = gear_0\left(\frac{\partial l_i}{\partial \pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega$$

---

siteトランスミッション：refsiteが指定されていない場合

　①アクチュエータ長 $l_i$ ： $l_i = 0$ です。

　②アクチュエータのモーメント $N_i$ ：site座標系からワールド座標系への回転行列を $R_\mathrm{site}$ とします。また $\pmb{gear}$ の第1～3要素のベクトル、第4～6要素のベクトルをそれぞれ $\pmb{gear}_\mathrm{trans}$ 、 $\pmb{gear}_\mathrm{rot}$ を $\pmb{gear}$ とします。このとき、ワールド座標系におけるgear要素 $\pmb{g}_\mathrm{trans},\pmb{g}_\mathrm{rot}\in\mathbb{R}^3$ をそれぞれ

$$\pmb{g}_\mathrm{trans} = R_\mathrm{site}\pmb{gear}_\mathrm{trans},\space \pmb{g}_\mathrm{rot} = R_\mathrm{site}\pmb{gear}_\mathrm{rot}$$

と定義できます。次に、siteの並進/回転ヤコビ行列をそれぞれ $J_\mathrm{s,trans},J_\mathrm{s,rot}$ とします（ $(3\times n_v)$ 行列）。このとき、アクチュエータのモーメント $N_i\in\mathbb{R}^{n_v}$ は次のように書けます。

$$N_i = J_\mathrm{s,trans}^\mathsf{T}\pmb{g}_\mathrm{trans} + J_\mathrm{s,rot}^\mathsf{T}\pmb{g}_\mathrm{rot}$$

　③アクチュエータ速度 $\dot{l_i}$ ：各自由度ごとの速度 $\pmb{q}_\mathrm{vel}\in\mathbb{R}^{n_v}$ を用いて、以下の式で計算されます。

$$\dot{l_i} = N_i\cdot\pmb{q}_\mathrm{vel}$$

---

siteトランスミッション： refsiteが指定されている場合

　①アクチュエータ長 $l_i$ ：siteとrefsiteの中心位置、クォータニオンをそれぞれ $\pmb{x}_\mathrm{site}, \pmb{x}_\mathrm{ref}$ 、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ とします。後述のクォータニオンの差分から角速度を求める方法を応用して角度差 $\pmb{\omega}$ を求めます。これらから、アクチュエータ長 $l_i$ は次のように求められます。

$$l_i = \pmb{gear}_\mathrm{trans}\cdot(\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}) + \pmb{gear}_\mathrm{rot}\cdot\pmb{\omega}$$

もしくは $(\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref})$ と $\pmb{\omega}$ をまとめてベクトル $\pmb{\chi}\in\mathbb{R}^6$ とすれば、以下のように書くこともできます。

$$l_i = \pmb{gear}\cdot\pmb{\chi}\space\space \mathrm{where}\space\space \pmb{\chi} = \begin{bmatrix}\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}\ \pmb{\omega}\end{bmatrix}$$

　②アクチュエータのモーメント $N_i$ ：上で定義したヤコビアンに加え、refsiteの並進/回転ヤコビ行列をそれぞれ $J_\mathrm{r,trans}',J_\mathrm{r,rot}'$ とします（ $(3\times n_v)$ 行列）。これを用いて、以下のような $J_\mathrm{trans},J_\mathrm{rot}$ を定義します。ただし、共通の祖先DOFについては、それとその親チェーンの列の値を $[0\space 0\space 0]^\mathsf{T}$ に設定します。

$$J_\mathrm{trans} = J_\mathrm{s,trans} - J_\mathrm{r,trans},\space\space\space J_\mathrm{rot} = J_\mathrm{s,rot} - J_\mathrm{r,rot}$$

このとき、アクチュエータのモーメント $N_i\in\mathbb{R}^{n_v}$ は次のように書けます。

$$N_i = J_\mathrm{trans}^\mathsf{T}\pmb{g}_\mathrm{trans} + J_\mathrm{rot}^\mathsf{T}\pmb{g}_\mathrm{rot}$$

　③アクチュエータ速度 $\dot{l_i}$ ：各自由度ごとの速度 $\pmb{q}_\mathrm{vel}\in\mathbb{R}^{n_v}$ を用いて、以下の式で計算されます。

$$\dot{l_i} = N_i\cdot\pmb{q}_\mathrm{vel}$$

---

クォータニオンの差分から角速度を求める方法

　二つのクォータニオン $q_a,q_b$ の差分から、角速度ベクトル $\pmb{\omega}$ を求める方法について説明します（関数mj_quat2Vel）。

　はじめに、 $q_b$ の逆元 $\bar{q_b}$ と $q_a$ を乗算して、相対回転クォータニオン $q_\mathrm{dif}$ を取得します。

$$q_\mathrm{dif} = \bar{q_b} \otimes q_a$$

　この $q_\mathrm{dif}$ の虚部ベクタ $\pmb{q}_\mathrm{dif} = (x\sin{\theta/2},\space y\sin{\theta/2},\space z\sin{\theta/2})$ を正規化し、回転軸 $\pmb{a}$ を取得します。

$$\pmb{a} = \frac{\pmb{q}_\mathrm{dif}}{||\pmb{q}_\mathrm{dif}||}$$

また、 $q_\mathrm{dif}$ の実部 $q_\mathrm{dif}^w$ を利用して、回転角 $\theta$ を計算します。このとき、回転角 $\theta$ は $-\pi<\theta\leq \pi$ の範囲に収まるようにします。

$$\theta = 2\tan^{-1}\left(\frac{\sin(\theta/2)}{q_\mathrm{dif}^w}\right) = 2\tan^{-1}\left(\frac{||\pmb{q}_\mathrm{dif}||}{q_\mathrm{dif}^w}\right)$$

回転角 $\theta$ をタイムステップ $\Delta t$ で割って角速度とします。関数mj_quat2Velでは、 $\Delta t \equiv 1$ です。

$$\pmb{\omega} = \frac{\theta}{\Delta t}\pmb{a} = \theta\pmb{a}$$

---

joint/tendonトランスミッション

　jointトランスミッションはjoint属性を指定することで選択されるトランスミッションです。ジョイントのタイプにより挙動が変化します。ここで $gear_1$ をgear属性の第一要素と定義します。

• "hinge"と"slide"
  • シンプルな挙動をします。"hinge"の場合はよくあるモータ、"slide"の場合は直動モータです。
  • アクチュエータ長 $l_i(q)$ はジョイントの位置/角度と $gear_1$ の積となります。
• "ball"
  • gear属性の最初の３つの要素は、アクチュエータがトルクを生成する子フレーム内の3D回転軸を定義します。
  • アクチュエータ長さ $l_i(q)$ は、このギア軸とジョイントの角度軸表現（クォータニオン定義）との内積として定義されます。
    • gearが正規化されている場合 $l_i(q)$ の単位はラジアンです
    • 回転が $\pi$ を超えると $-\pi$ に転じ、その逆も同じように変化します。
    • このため、ボールジョイントの<position>サーボはこの巻き付きを防ぐように制限が必要です。
• "free"
  • gear属性の最初の３つの要素はワールド座標系での移動軸を定義し、次の３要素でローカル座標系での回転軸を定義します。
  • アクチュエータは指定された軸に対して力とトルクを生成します。
  • アクチュエータの長さ $l_i(q)=0$ であるため、<position>サーボでは使用できません。

　tendonトランスミッションはtendon属性を指定することで選択されるトランスミッションです。指定すると、アクチュエータは指定された腱に作用します。アクチュエータの長さ $l_i(q)$ は腱の長さとギア比（おそらく $gear_1$ ）の積に比例します。

slider-crank トランスミッション

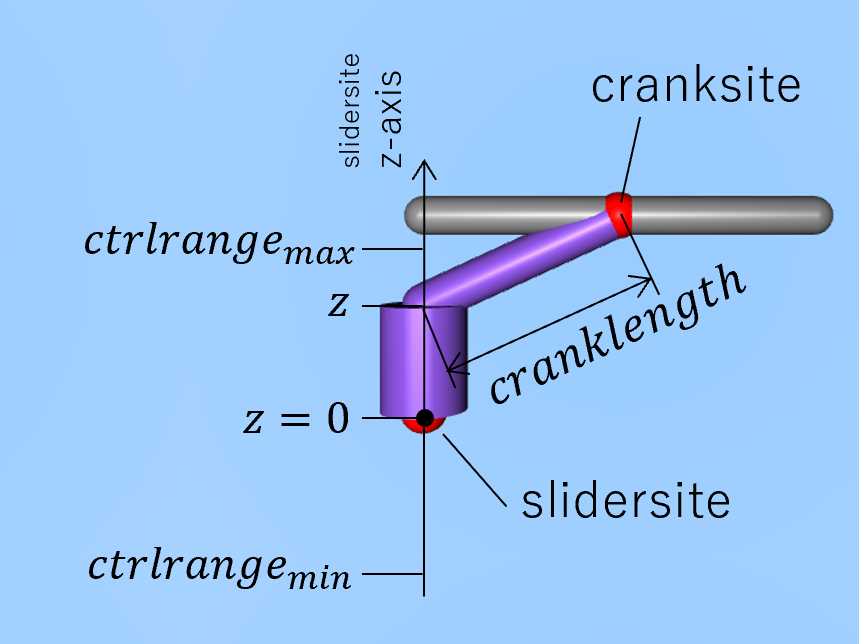
　slider-crankトランスミッションは直線運動からトルクを生成するための伝達機構です。本トランスミッションを備えたモデルの概観と動作図を以下に示します。実装の詳細は下記「簡易なslider-crank実装」を参照してください。

図 slider-crankトランスミッション（左）slider-crankで指定する各属性とモデル寸法の関係（右）動作．アクチュエータの機構（紫の部分）は接触判定を持ちません．

　各属性と寸法の対応関係を上図左に示しました。

• cranklength
  • コネクティングロッド（コンロッド）の長さを指定します
  • コンロッドの長さを示すため、正の値である必要があります。
• cranksite
  • クランクとコネクティングロッドを結合するピンを指定します
• slidersite
  • スライダーとコネクティングロッドを結合するピンを指定します
  • スライダーは自身の座標系Z軸に沿い動くため、部位はキネマティックツリーで定義する際に必要に応じて向きを指定する必要があります。アクチュエータ側の定義でその向きを変更することはできません
• ctrlrange
  • 制御入力の範囲を指定します
  • <position>の場合、制御入力の範囲がそのままスライダーの可動範囲を意味します。例えば"-1 1"を指定した場合、スライダーは下/上に $-1\space\mathrm{m}$ / $1\space\mathrm{m}$ ずつ動かすことが可能です※

※：実際には「制御入力 $u_i$ の変化がなめらかなとき、アクチュエータの動作開始からある程度時間がたつと $z\simeq u_i$ となる」という説明が正しいかと思います。というのも、アクチュエータ速度の初期値が $0$ であるため、初めのうちは $u_i$ に $z$ が追従しきれないためです。

正確に言えば、前述したように $z = \pmb{a}\cdot\pmb{v}_\mathrm{rod} - \sqrt{(\pmb{a}\cdot\pmb{v}_\mathrm{rod})^2 + r^2 - |\pmb{v}_\mathrm{rod}|^2}$ です。このため、見た目以上にこのアクチュエータの操作は難しいです。

　以下のモデルをもとに各属性について見てみましょう。slidersiteは直線運動の基準を示しており、スライダー（上下に動いている円柱）はこの点を原点として動作します。直線運動は"slidersite"のZ軸に沿って行われ、その下限と上限はctrlrangeにより定められます。"slidersite"の座標系は $y$ 軸正の向きを $z$ 軸と定めていますから、スライダーは $y$ 軸方向に動区ことになります。また、この直線運動がコンロッド（細長い紫カプセル）により"cranksite"に伝えられることで、クランク部（灰色）は回転運動を行います。

<actuator>
  <position name="slider-crank" cranksite="cranksite" slidersite="slidersite" cranklength=".11" ctrllimited="true" ctrlrange="-.1 .1" kp="30"/>
</actuator>

　上記アクチュエータで指定されている"cranksite"と"slidersite"の実装を以下に示します。ここで、以下の実装では一部の属性等を省略していることに注意してください。こちらも詳細は下記「簡易なslider-crank実装」を参照してください。

<worldbody>
  ...
  <site name="slidersite" pos="0 -.1 0" zaxis="0 1 0" ... rgba="1 0 0 1"/>
  <body>
    <joint damping=".1"/>
    ...
    <site name="cranksite" pos=".1 0 0" ... rgba="1 0 0 1"/>
  </body>
</worldbody>

【簡易なslider-crank実装】

　以下のモデルはHow to correctly use slider-crank transmission for cylinders? #374を参照しました。当該記事はMuJoCoのメンテナーが解答を行ったQ&Aであり、以下のモデルの他にもslider-crankトランスミッションを扱う際に参考になる事項がいくつか書かれています。

　以下のPythonコードに示すように、本プログラムは振幅を $0.8$ 、周期を $\pi\space\mathrm{s}$ の正弦波を制御入力としています。

図 制御入力

simple_slider_crank.xml

<mujoco>
  <worldbody>
    <light pos="0 0 1"/>
    <camera name="front" pos=".1 0 .4" xyaxes="1 0 0 0 1 0"/>
    <site name="slidersite" pos="0 -.1 0" zaxis="0 1 0" size=".012" rgba="1 0 0 1"/>
    <body>
      <joint damping=".1"/>
      <geom type="capsule" size=".01" fromto="0 0 0 .2 0 0"/>
      <site name="cranksite" pos=".1 0 0" size=".012" rgba="1 0 0 1"/>
    </body>
  </worldbody>

  <actuator>
    <position name="slider-crank" cranksite="cranksite" slidersite="slidersite" cranklength=".11" ctrllimited="true" ctrlrange="-.1 .1" kp="30"/>
  </actuator>
</mujoco>

# model, data, rendererを取得
...

# 動画をレンダリングする
fps = 30
frames = []
for i in range(n_frames):
    while data.time * fps <= i:
        # 振幅0.8、周期 $\pi\space\mathrm{s}$ の正弦波を制御入力とする
        d.ctrl[0] = 0.8 * np.sin(2*data.time)

        mujoco.mj_step(model, data)

    renderer.update_scene(data, camera="front")
    frames.append(renderer.render())
save_video(frames, "output.mp4", fps)

bodyトランスミッション

　bodyトランスミッションを持つアクチュエータは接触点に接触法線方向の線形力を加えることができます。簡単にいうとヤモリの足や吸盤、磁石のような「吸着する物体」をシミュレートできます。接続対象は<body>であり、そのボディに接触したすべての物体は吸い寄せられるようになります（制御入力ONのとき）。

　bodyトランスミッションはアクチュエータ要素<adhesion>の伝達形式です。以下に<adhesion>を使用した例を示します。左右の図それぞれについて、右側のアームには吸着力が発生しており、アームを持ち上げた際に赤い立方体が持ち上がっていることがわかります。また、あくまでこのアクチュエータは接線力を生成するだけであるため、出力力/トルクによっては持ち上がらないこともあります（強制的に接合するわけではない）。

制御入力 90	制御入力 100

図 bodyトランスミッションの例．各図左が<adhesion>なし、各図右が<adhesion>あり．左図は<adhesion>の制御入力 $90$ 、右は制御入力 $100$ ．制御入力の強さによっては十分持ち上がらないこともある

　<adhesion>アクチュエータの簡単な使用方法を以下に示します。<adhesion>について必ず指定する必要のある属性はbodyとctrlrangeです。bodyでは吸着力を生じさせるボディを指定し、ctrlrangeでは制御入力の範囲を正値で指定します。

<worldbody>
  <body name="arm">
    ...
  </body>
</worldbody>

<actuator>
  <adhesion body="arm" ctrlrange="0 500"/>
</actuator>

【実装コード詳細】

<mujoco>
  <asset>
    <texture type="skybox" builtin="gradient" rgb1="1 1 1" rgb2=".6 .8 1" width="256" height="256"/>
    <texture name="grid" type="2d" builtin="checker" rgb1=".1 .2 .3"
     rgb2=".2 .3 .4" width="300" height="300" mark="none"/>
    <material name="grid" texture="grid" texrepeat="1 1"
     texuniform="true" reflectance=".2"/>
  </asset>
  
  <worldbody>
    <light directional="true"/>
    <camera name="fixed" pos="0 -2 1" zaxis="0 -2 1"/>
    <geom type="plane" size="10 10 5" material="grid"/>
    <body name="leftarm">
      <joint name="left" type="slide" pos="-.35 0 .5"/>
      <geom type="cylinder" size=".03" density="50" fromto="-.35 0 .5 -.35 0 1.5"/>
      <geom type="cylinder" size=".2" fromto="-.35 0 .5 -.35 0 .505" rgba="1 .5 0 1"/>
    </body>
    <body name="rightarm">
      <joint name="right" type="slide" pos=".35 0 .5"/>
      <geom type="cylinder" size=".03" density="50" fromto=".35 0 .5 .35 0 1.5"/>
      <geom type="cylinder" size=".2" fromto=".35 0 .5 .35 0 .505" rgba="1 .5 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".2 .2 .2" pos="-.35 0 .2" density="50" rgba="1 0 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".2 .2 .2" pos=".35 0 .2" density="50" rgba="1 0 0 1"/>
    </body>
  </worldbody>

  <actuator>
    <motor joint="left"/>
    <motor joint="right"/>
    <adhesion body="rightarm" ctrlrange="0 500"/>
  </actuator>
</mujoco>

# model, data, rendererを取得
...

# 右側のアームについて吸着力を設定
data.ctrl[2] = 100

# 動画をレンダリングする
fps = 30
frames = []
for i in range(n_frames):
    while data.time * fps <= i:
      mujoco.mj_step(model, data)
    
    if i > 0.2*fps: # 0.2秒経過後 : アームと立方体が接触
        # 左右のアームを上方向に動かす
        data.ctrl[0] = 50
        data.ctrl[1] = 50
    
    renderer.update_scene(data)
    frames.append(renderer.render())
save_video(frames, "output.mp4", fps)

siteトランスミッション

　指定した<site>を力点とし、その<site>座標系に従った力/トルクを加えることができるアクチュエータを作成します。refsite属性も併せて指定されている場合、refsiteの座標系に従い力/トルクが与えられます。例えば飛行機の後方向への力をシミュレートするなど、ジェットやプロペラをモデル化する際などに役立ちます。

　（<adhesion>&<cylinder>を除く？）アクチュエータででsiteトランスミッションを使用することを考えます。このとき、gear属性の値 $(x,y,z,r_x,r_y,r_z)$ は次のように解釈されます

• $r_x,r_y,r_z=0$ のとき
  • $(x,y,z)$ は力を与える方向と、制御入力のゲイン $\sqrt{x^2+y^2+z^2}$ を示す
  • 例: gearが"3 4 0"または"3 4 0 0 0 0"の<motor>: xy面右上方向に $5 u_i\space\mathrm{N}$ の力を与える
• $x,y,z=0$ のとき
  • $(r_x,r_y,r_z)$ はトルクを与える軸と、制御入力のゲイン $\sqrt{r_x^2+r_y^2+r_z^2}$ を示す
  • 例: gearが"0 0 0 1 1 1"の<motor>: 回転軸は $x=y=z$ 、トルクは $\sqrt{3} u_i\space\mathrm{Nm}$

　さて、これを以下の例とともに見ていきましょう。以下は自由落下する $1\space\mathrm{kg}$ の立方体に対し、siteトランスミッションによる力を加えたものです。力の加え方は左から順に

• (赤): 自由落下
• (緑): y軸方向(奥)に<motor>, $u_i=50$
• (青): z軸方向(上)に<motor>, $u_i=50$
• (紫): y軸周りに<motor>, $u_i=5$
• (黄): z軸方向(上)に<dumper>, $u_i=10$
• (縹): y軸方向(奥)に<dumper>, $u_i=10$

となっています。以下の動画と比較すると、想定通りに動いていることがわかります。このうち、特に注目したいのが一番右（縹色）の落下です。<dumper>は速度に負比例した力を出力するアクチュエータですが、下図では一番右（赤色）の自由落下と同じ落ち方をしていることがわかります。このように、変位や速度を参照するアクチュエータでは、gearで指定した軸の速度のみが参照されます。今回の実験では $y$ 軸方向への移動速度は $0$ であったため、<dumper>の出力は $p_5=0$ となったわけです。

図 siteトランスミッションによる動作．画面上方向が $z$ 軸、奥方向が $y$ 軸．灰色の線は初期状態の各重心を通る鉛直な線

【実装コード詳細】

<mujoco>
  <asset>
    <texture type="skybox" builtin="gradient" rgb1="1 1 1" rgb2=".6 .8 1" width="256" height="256"/>
  </asset>

  <worldbody>
    <light directional="true"/>
    <light directional="true" dir="0 0 1"/>
    <site type="cylinder" size=".01 3" pos="-1 0 0" rgba="0 0 0 .3"/> 
    <site type="cylinder" size=".01 3" pos="-.6 0 0" rgba="0 0 0 .3"/> 
    <site type="cylinder" size=".01 3" pos="-.2 0 0" rgba="0 0 0 .3"/> 
    <site type="cylinder" size=".01 3" pos=".2 0 0" rgba="0 0 0 .3"/> 
    <site type="cylinder" size=".01 3" pos=".6 0 0" rgba="0 0 0 .3"/> 
    <site type="cylinder" size=".01 3" pos="1 0 0" rgba="0 0 0 .3"/> 
    <camera name="fixed" pos="0 -2 .5" xyaxes="1 0 0 0 0 1"/>
    <body>
      <freejoint/>
      <geom type="box" size=".1 .1 .1" pos="-1 0 1" rgba="1 0 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".1 .1 .1" pos="-.6 0 1" rgba="0 1 0 1"/>
      <site name="f1" size=".01" pos="-.6 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".1 .1 .1" pos="-.2 0 1" rgba="0 0 1 1"/>
      <site name="f2" size=".01" pos="-.2 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".1 .1 .1" pos=".2 0 1" rgba="1 0 1 1"/>
      <site name="f3" size=".01" pos=".2 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".1 .1 .1" pos=".6 0 1" rgba="1 1 0 1"/>
      <site name="f4" size=".01" pos=".6 0 1"/>
    </body>
    <body>
      <freejoint/>
      <geom type="box" size=".1 .1 .1" pos="1 0 1" rgba="0 1 1 1"/>
      <site name="f5" size=".01" pos="1 0 1"/>
    </body>
  </worldbody>

  <actuator>
    <motor site="f1" gear="0 1 0"/>
    <motor site="f2" gear="0 0 1"/>
    <motor site="f3" gear="0 0 0 0 1 0"/>
    <damper site="f4" kv="10" ctrlrange="0 1" gear="0 0 3"/>
    <damper site="f4" kv="10" ctrlrange="0 1" gear="0 3 0"/>
  </actuator>
</mujoco>

　また、アクチュエータによる力/トルクは<site>の重心に対して働き、参照値も<site>の変位/速度を基準とします（<refsite>を指定している場合はそちら）。このため、<site>の位置によっては同じ制御入力・同じ属性値であっても違う挙動となる可能性があります。

　以下は上と同じ立方体に対して、<motor>で力を加えた例です。左は立方体の重心位置に<site>が位置し、右は立方体の左側（黒い点）に位置しています。どちらもgear="0 0 1"としており、上方向への力が働いています。緑の立方体は力点が重心位置ではないため、アクチュエータにより重心周りのトルクが生じます。このため、緑の立方体は回転しながら落下しました。

図 siteトランスミッションによる動作（左）<site>は立方体の重心に位置（右）<site>は立方体の左方向に位置（黒点）

actuator詳説 : 活性化ダイナミクス

　内部状態 (活性化状態) $w_i$ を持つアクチュエータについては、力生成の前段階として活性化状態の計算が存在します。すべての活性化状態はその（各タイムステップごとの）変化分 $\dot{w_i}$ により定義され、各ステップごとに $w_i$ が計算されます。シミュレーション全体を通して変化しない定数を無視した場合、変化分 $\dot{w_i}$ は次４パラメタを持つ関数として考えることができます。

$$\dot{w_i} = \dot{w_i}(u_i,w_i,l_i,\dot{l_i})$$

ここで、シミュレーション全体を通して変化しない定数とは、タイムステップ幅 $h$ 、活性化パラメタdynprm（ $\pmb{dyn}$ ）を指します。上の関数の中にはこれらも含まれていますが、シミュレーション中に変化することはないためパラメタとしては省略しています。

　さて、dyntypeと活性化状態 $w_i$ の関係を以下に示します（"user"を除く）。ここで、 $w_{i,t}$ はタイムステップ $t$ での $w_i$ の値を意味します。また、"filter"と"filterexact"での $dyn_0$ は各アクチュエータ固有の時定数 $\mathtt{t}$ に相当し、"muscle"の $\pmb{dyn}$ のうち第1,2要素はそれぞれ時定数 $\tau_{act}, \tau_{deact}$ に相当します。

表 dyntypeと活性化状態 $w_i$ の更新式

dyntype	更新式	変化分の定義
none	活性化状態なし
integrator	$w_{i,t+1} = w_{i,t} + hu_{i,t}$	$\dot{w_i} = u_i$
filter	$w_{i,t+1} = w_{i,t} + h(u_{i,t}-w_{i,t})/ dyn_0$	$\dot{w_i} = (u_i-w_i)/dyn_0$
filterexact	$w_{i,t+1} = w_{i,t} + (u_{i,t}-w_{i,t})(1-e^{-h/dyn_0})$	$\dot{w_i} = (u_i-w_i)/dyn_0$
muscle	$w_{i,t+1} = w_{i,t} + hf_{muscleDyn}(u_i,w_i,\pmb{dyn})$ $f_{muscleDyn}(\cdot)$ は関数mujoco.mju_muscleDynamics、詳細は後述	$\dot{w_i}=f_{muscle}(\cdot)$

更新式は変化分 $\dot{w_i}$ を積分することにより計算されます。"filterexact"のみ厳密な積分（exact integrator）であり、ほかはオイラー法による数値積分を使用しています。

　組み込みのアクチュエータショートカットと各dyntypeの関係は以下の通りです。ここからわかるように、組み込みのアクチュエータを使用する限りdynprmの４要素目以降は不要です。

表 dyntypeと（組み込みの）アクチュエータショートカット

dyntype	使用するdynprm	(組み込みの)ショートカット
none	なし	<motor>, <position>, <velocity>, <damper>, <adhesion>
integrator	なし	<intvelocity>
filter	$dyn_0$ (=時定数 $\mathtt{t}$ )	<cylinder>
filterexact	$dyn_0$ (=時定数 $\mathtt{t}$ )	なし
muscle	$dyn_0 \sim dyn_2$ (= $\tau_{act},\tau_{deact},\tau_{smooth}$ )	<muscle>

アクチュエータのactearlyパラメタが"true"に設定されている場合、mjData.actuator_force[i]は次の活性化状態 $w_{i,t+1}$ に基づき計算されます。このとき制御入力 $u_i$ の変化と加速度への影響との間の遅延が1ステップ分減少するため、全体のダイナミクスは３次から２次へと減少します。

actuator詳説 : 力生成メカニズム

　各アクチュエータはスカラーの力/トルク $p_i$ を生成します。活性化状態の計算と同様に $p_i$ は４つのパラメタの関数であり（ $p_i(u_i,w_i,l_i,\dot{l}_i)$ ）、以下の式により記述されます。

$$p_i = Gain\times(w_i\space or \space u_i) + Bias$$

　活性化ダイナミクスと同様に、 $Gain,Bias$ はそれぞれgainprm,biasprmから計算されます。このgaintypeとゲイン(係数) $Gain$ の関係、およびbiasprmとバイアス項 $Bias$ の関係を以下に示します（"user"を除く）。

表 gaintypeとゲイン(係数) $Gain$ との対応関係

gaintype	式
fixed	$Gain = gain_0$
affine	$Gain = gain_0 + gain_1\times l_i + gain_2\times \dot{l_i}$
muscle	$Gain = f_{muscleGain}(l_i,\dot{l_i},lengthrange_i,acc0_i,\pmb{gain})$ $f_{muscleGain}(\cdot)$ は関数mujoco.mju_muscleGain、詳細は後述

表 biastypeとバイアス項 $Bias$ との対応関係

biastype	式
none	$Bias=0$
affine	$Bias = bias_0 + bias_1\times l_i + bias_2\times \dot{l_i}$
muscle	$Bias = f_{muscleBias}(l_i,lengthrange_i,acc0_i,\pmb{gain})$ $f_{muscleBias}(\cdot)$ は関数mujoco.mju_muscleBias、詳細は後述

　このようにして算出された出力トルク/力 $p_i$ は、トランスミッションで決定された力の分配規則に従い、実際のトルク/力として作用します。この例を以下に示します。また、複数のアクチュエータが一つの対象に作用するとき、すべてのアクチュエータの出力は合算されて作用します。この一般化座標での正味の力はmjData.qfrc_actuatorに格納されます。

• $i$ 番目のアクチュエータのターゲットががヒンジジョイント
  • 出力は単純な関節トルク $p_i\space\mathrm{[Nm]}$ として作用します
• $i$ 番目のアクチュエータがsiteトランスミッション（refsiteの指定はなし）
  • 出力はgearで定められた軸方向/周りに力/トルク $p_i\space\mathrm{[N]/[Nm]}$ を与えます（作用点は<site>の重心位置）
  • 例えばgear="0 0 3"であれば、<site>の座標系の $z$ 軸方向に力 $p_i\space\mathrm{[N]}$ を加えます
  • またgear="0 0 0 1 0 0"であれば、`の座標系の $x$ 軸回りにトルク $p_i\space\mathrm{[Nm]}$ を加えます

アクチュエータモデルのまとめ

　ここまでで、アクチュエータの動作を決定する３要素「トランスミッション」、「活性化ダイナミクス」、「力生成メカニズム」についての説明を行いました。本節ではこれを簡単にまとめたものを以下に示します。時刻を付したもの（ $u_{i,t}$ ）を除き、以下はいずれも時刻 $t$ における入出力 $u_i,p_i$ 、変位/角度 $x/\theta$ 、速度/角速度 $v/\omega$ です。ただし、各ショートカットの固有の属性（ $k_p,k_v$ 等）へ規定値を代入していないものについては、下表の下「上表の詳細：固有の属性値（kp,kv等）を変更する場合」を参照してください。

ただし、<muscle>アクチュエータについてはさらに複雑であるため後述します。また、jointトランスミッションに関する変数については下表の下を参照してください。

表 アクチュエータショートカット・トランスミッションの組合せとその出力トルク/力． $k_p,k_v$ 等の値は各ショートカットの規定値を適用しました。

タイプ	伝達方式	説明
<motor>	joint	$p_i = u_i$
<position>	site	$\pmb{x}_\mathrm{site}, \pmb{x}_\mathrm{ref}$ 、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ はそれぞれsiteとrefsiteの中心位置、クォータニオンです。また、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ の差分を $\pmb{\omega}\in\mathbb{R}^3$ と定義しています。 　　 $p_i = u_i - \pmb{gear}\cdot\begin{bmatrix}\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}\ \pmb{\omega}\end{bmatrix}$
〃	joint	"hinge" : $p_i = u_i - gear_0\space\theta$ "slide" : $p_i = u_i - gear_0\space x$ "ball"- : $p_i = u_i - |\pmb{gear}|(\pmb{n} \cdot \pmb{n_{gear}})\space \theta$ 　　　　 $\big(where\space \theta\in[-\pi,\pi] \big)$ "free"- : $p_i = u_i$
〃	slider-crank	$\pmb{a}\in\mathbb{R}^3$ はslidersiteの $z$ 軸ベクトル、 $\pmb{v}_\mathrm{rod}\in\mathbb{R}^3$ はslidersiteからcranksiteまでのベクトル、 $r$ はcranklengthです。また、 $\theta,\omega$ はcranksiteを取り付けたボディのヒンジジョイントの角度/角速度です。 　　 $p_i = u_i - gear_0\space z$ また、<position>アクチュエータの場合に時刻 $t>>0$ で $z\simeq u_i$ となると仮定すれば以下のようになります。詳細は計算を参照してください。 　　 $p_i\simeq (1 - gear_0)u_i$
<velocity>	joint	"hinge" : $p_i = u_i - gear_0\space\omega$ "slide" : $p_i = u_i - gear_0\space v$ "ball"- : $p_i = u_i - |\pmb{gear}||\pmb{\omega}|$ "free"- : $p_i = u_i - \pmb{gear}\cdot \pmb{v}$
<intvelocity> ※1	joint	"hinge" : $p_i = h\sum_{n=0}^{t-1}u_{i,n} - gear_0\space\theta$ "slide" : $p_i = h\sum_{n=0}^{t-1}u_{i,n} - gear_0\space x$ "ball"- : $p_i = h\sum_{n=0}^{t-1}u_{i,n} - |\pmb{gear}|(\pmb{n} \cdot \pmb{n_{gear}})\space \theta$ 　　　　 $\big(where\space \theta\in[-\pi,\pi] \big)$ "free"- : $p_i = h\sum_{n=0}^{t-1}u_{i,n}$
<damper>	joint	"hinge" : $p_i = - (gear_0\space\omega)\space u_i$ "slide" : $p_i = - (gear_0\space v)\space u_i$ "ball"- : $p_i = - |\pmb{gear}||\pmb{\omega}|\space u_i$ "free"- : $p_i = - (\pmb{gear}\cdot \pmb{v})\space u_i$
<cylinder>	joint	"hinge" : $p_i = h \sum_{n=0}^{t-1}\big(1-h\big)^n u_{i,n}$ "slide" : $p_i = h \sum_{n=0}^{t-1}\big(1-h\big)^n u_{i,n}$ "ball"- : $p_i = h \sum_{n=0}^{t-1}\big(1-h\big)^n u_{i,n}$ 　　　　（ $where\space \theta\in[-\pi,\pi]$ ） "free"- : $p_i = h \sum_{n=0}^{t-1}\big(1-h\big)^n u_{i,n}$
<adhesion>	body	$p_i = u_i$

【上表の詳細：固有の属性値（kp,kv等）を変更する場合】

表 アクチュエータショートカット・トランスミッションの組合せとその出力トルク/力． $k_p,k_v$ 等の固有の属性を変更する場合

タイプ	伝達方式	説明
<motor>	joint	$p_i = u_i$
<position>	site	$\nabla l_i$ はアクチュエータのモーメント、 $\pmb{q}_\mathrm{vel}\in\mathbb{R}^{n_v}$ は各自由度ごとの速度です。また、siteとrefsiteの中心位置、クォータニオンをそれぞれ $\pmb{x}_\mathrm{site}, \pmb{x}_\mathrm{ref}$ 、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ とし、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ の差分を $\pmb{\omega}\in\mathbb{R}^3$ と定義しています。 　　 $p_i = k_p u_i - k_p\space l_i - k_v(\nabla l_i \cdot \pmb{q}_\mathrm{vel})$ 　　 $\left(\mathrm{where}\space l_i = \pmb{gear}\cdot\begin{bmatrix}\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}\ \pmb{\omega}\end{bmatrix}\right)$
〃	joint	"hinge" : $p_i = k_pu_i - gear_0(k_p\space\theta + k_v\space\omega)$ "slide" : $p_i = k_pu_i - gear_0(k_p\space x + k_v\space v)$ "ball"- : $p_i = k_p u_i - |\pmb{gear}|\big(k_p(\pmb{n} \cdot \pmb{n_{gear}})\space \theta + k_v|\pmb{\omega}|\big)$ 　　　　 $\big(where\space \theta\in[-\pi,\pi] \big)$ "free"- : $p_i = k_p u_i - k_v\space \pmb{gear}\cdot \pmb{v}$
〃	slider-crank	$\pmb{a}\in\mathbb{R}^3$ はslidersiteの $z$ 軸ベクトル、 $\pmb{v}_\mathrm{rod}\in\mathbb{R}^3$ はslidersiteからcranksiteまでのベクトル、 $r$ はcranklengthです。また、 $\theta,\omega$ はcranksiteを取り付けたボディのヒンジジョイントの角度/角速度です。 　　 $p_i = k_p u_i - k_p\space gear_0\space z - k_v\space gear_0\left(\frac{\partial l_i}{\partial \pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega$ また、<position>アクチュエータの場合に時刻 $t>>0$ で $z\simeq u_i$ となると仮定すれば以下のようになります。詳細は計算を参照してください。 　　 $p_i\simeq (k_p - k_p\space gear_0)u_i - k_v\space gear_0\left(\frac{\partial l_i}{\partial \pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega$
<velocity>	joint	"hinge" : $p_i = k_v (u_i - gear_0\space\omega)$ "slide" : $p_i = k_v (u_i - gear_0\space v)$ "ball"- : $p_i = k_v (u_i - |\pmb{gear}||\pmb{\omega}|)$ "free"- : $p_i = k_v (u_i - \pmb{gear}\cdot \pmb{v})$
<intvelocity> ※1	joint	"hinge" : $p_i = k_p h\sum_{n=0}^{t-1}u_{i,n} - gear_0(k_p\space\theta + k_v\space\omega)$ "slide" : $p_i = k_p h\sum_{n=0}^{t-1}u_{i,n} - gear_0(k_p\space x + k_v\space v)$ "ball"- : $p_i = k_p h\sum_{n=0}^{t-1}u_{i,n} - |\pmb{gear}|\big(k_p(\pmb{n} \cdot \pmb{n_{gear}})\space \theta + k_v|\pmb{\omega}|\big)$ 　　　　 $\big(where\space \theta\in[-\pi,\pi] \big)$ "free"- : $p_i = k_p h\sum_{n=0}^{t-1}u_{i,n} - k_v\space \pmb{gear}\cdot \pmb{v}$
<damper>	joint	"hinge" : $p_i = -k_v (gear_0\space\omega)\space u_i$ "slide" : $p_i = -k_v (gear_0\space v)\space u_i$ "ball"- : $p_i = -k_v |\pmb{gear}||\pmb{\omega}|\space u_i$ "free"- : $p_i = -k_v (\pmb{gear}\cdot \pmb{v})\space u_i$
<cylinder>	joint	$A$ はシリンダの面積（area属性）、 $\tau$ は活性化ダイナミクスの時定数（timeconst属性）、 $b_j$ はbias属性のパラメタ $(j=0,1,2)$ です。diameter属性( $d$ )を指定した場合は、 $A:=\pi d^2/4$ として定義されます。 "hinge" : $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 + gear_0(b_1\space\theta + b_2\space\omega)$ "slide" : $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 + gear_0(b_1\space x + b_2\space v)$ "ball" : $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n}$ 　　　　　　　 $+ b_0 + |\pmb{gear}|\big(b_1(\pmb{n} \cdot \pmb{n_{gear}})\space \theta + b_2|\pmb{\omega}|\big)$ 　　　　　　　（ $where\space \theta\in[-\pi,\pi]$ ） "free" : $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 - b_2\space \pmb{gear}\cdot \pmb{v}$
<adhesion>	body	$p_i = gain_0 \times u_i$

※1 : actearly属性が"true"の場合、出力 $p_i$ 、変位/角度 $x/\theta$ 、速度/角速度 $v/\omega$ はすべて時刻 $t-1$ における値となります。

表 ジョイントのタイプとアクチュエータ長 $l_i$ /同速度 $\dot{l_i}$ ．

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。
"slide"	$x/v$ はそれぞれ関節変位/速度です。
"ball"	$\theta/\pmb{n}=(x,y,z)$ はそれぞれ回転角/方向ベクトル（クォータニオン表現）です。また $\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度、 $\pmb{n_{gear}}$ は $\pmb{gear}$ の単位ベクトルです。
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。

【ジョイントタイプとアクチュエータ長/速度】

表 ジョイントのタイプとアクチュエータ長 $l_i$ /同速度 $\dot{l_i}$ ．詳細はトランスミッション節を参照してください。

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。 　　 $l_i = gear_0\space\theta,\space\space\space \dot{l_i} = gear_0\space \omega$
"slide"	$x/v$ はそれぞれ関節変位/速度です。 　　 $l_i = gear_0\space x\space\space\space \dot{l_i} = gear_0\space v$
"ball"	$\theta/\pmb{n}=(x,y,z)$ はそれぞれ回転角/方向ベクトル（クォータニオン表現）です。また $\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度、 $\pmb{n_{gear}}$ は $\pmb{gear}$ の単位ベクトルです。 　　 $l_i = |\pmb{gear}|(\pmb{n} \cdot \pmb{n_{gear}})\space \theta$ （ $where\space \theta\in[-\pi,\pi]$ ） 　　 $\dot{l_i} = |\pmb{gear}||\pmb{\omega}|$
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。 　　 $l_i=0,\space\space \dot{l_i} = \pmb{v}\cdot \pmb{gear}$

計算の詳細：<motor>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (none, fixed, none)

　制御入力 $u_i$ が与えられたときの出力 $p_i$ は次の通りです。<motor>の場合、出力トルク/力 $p_i$ はgear属性に影響を受けません。

$$\begin{aligned}
p_i =& gain_0 \times u_i\
=& u_i
\end{aligned}$$

<motor> & jointトランスミッション

　jointトランスミッションについてアクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は上述のとおりです。したがって、本組合せでの入出力関係は以下のようになります。ここからわかるように、gear属性・アクチュエータ長/速度 $l_i/\dot{l_i}$ はいずれも入出力関係に影響しません。

$$p_i = u_i$$

計算の詳細：<position>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (none, fixed, affine)

　制御入力 $u_i$ が与えられたときの出力 $p_i$ は次の通りです。ここで、 $k_p$ は位置フィードバックゲイン（kp属性）、 $k_v$ はアクチュエータによる減衰（kv属性）です。

$$\begin{aligned}
p_i =& gain_0 \space u_i + bias_0 + l_i\space bias_1 + \dot{l_i}\space bias_2\\
=& k_pu_i - k_pl_i - k_v\dot{l_i}
\end{aligned}$$

<position> & siteトランスミッション

　<position>でsiteトランスミッションを使用するばあい、refsiteの指定が必要です。このとき、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は以下のように書けます。ここで、 $\nabla l_i$ はアクチュエータのモーメント、 $\pmb{q}_\mathrm{vel}\in\mathbb{R}^{n_v}$ は各自由度ごとの速度です。また、siteとrefsiteの中心位置、クォータニオンをそれぞれ $\pmb{x}_\mathrm{site}, \pmb{x}_\mathrm{ref}$ 、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ とし、 $\pmb{q}_\mathrm{site}, \pmb{q}_\mathrm{ref}$ の差分を $\pmb{\omega}$ としました。

$$l_i = \pmb{gear}\cdot\begin{bmatrix}\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}\\ \pmb{\omega}\end{bmatrix},\space\space\space \dot{l_i} = \nabla l_i\cdot\pmb{q}_\mathrm{vel}$$

したがって、本組合せでの入出力関係は以下のようになります。

$$p_i = k_p u_i - k_p\space l_i - k_v(\nabla l_i \cdot \pmb{q}_\mathrm{vel})\space\space\space\left(\mathrm{where}\space l_i = \pmb{gear}\cdot\begin{bmatrix}\pmb{x}_\mathrm{site} - \pmb{x}_\mathrm{ref}\\ \pmb{\omega}\end{bmatrix}\right)$$

<position> & jointトランスミッション

　jointトランスミッションについて、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は上述の通りです。したがって、本組合せでの入出力関係は以下のようになります。

表 ジョイントのタイプと入力 $u_i$ - 出力 $p_i$ 関係

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。 　　 $p_i = k_pu_i - gear_0(k_p\space\theta + k_v\space\omega)$
"slide"	$x/v$ はそれぞれ関節変位/速度です。 　　 $p_i = k_pu_i - gear_0(k_p\space x + k_v\space v)$
"ball"	$\theta/\pmb{n}=(x,y,z)$ はそれぞれ回転角/方向ベクトル（クォータニオン表現）です。また $\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度、 $\pmb{n_{gear}}$ は $\pmb{gear}$ の単位ベクトルです。 　　 $p_i = k_p u_i - |\pmb{gear}|\big(k_p(\pmb{n} \cdot \pmb{n_{gear}})\space \theta + k_v|\pmb{\omega}|\big)$ 　　（ $where\space \theta\in[-\pi,\pi]$ ）
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。 　　 $p_i = k_p u_i - k_v\space \pmb{gear}\cdot \pmb{v}$

<position> & slider-crankトランスミッション

　slider-crankトランスミッションについて、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は以下のように書けます。ここで、slidersiteの $z$ 軸ベクトルを $\pmb{a}\in\mathbb{R}^3$ 、slidersiteからcranksiteまでのベクトルを $\pmb{v}_\mathrm{rod}\in\mathbb{R}^3$ 、cranklengthを $r$ としました。また、 $\theta,\omega$ はcranksiteを取り付けたボディのヒンジジョイントの角度/角速度です。

$$\begin{aligned}l_i &= gear_0 \times z\\
\dot{l_i} &= gear_0\left(\frac{\partial l_i}{\partial \pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega
\end{aligned}$$

また、 $z$ はスライダー位置ですが、<position>アクチュエータの場合、時刻 $t>>0$ で $z\simeq u_i$ です（ $u_i$ がなめらかであれば…？）。

図 スライダー位置 $z$ と制御入力 $u_i$ ．約1.5秒以降はほとんど $z=u_i$ とわかる

これを前提に考えると、本組合せでの入出力関係は以下のようになります。

$$\begin{aligned}
p_i &= k_p u_i - k_p\space gear_0\space z - k_v\space gear_0\left(\frac{\partial l_i}{\partial \pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega\\\
&\simeq (k_p - k_p\space gear_0)u_i - k_v\space gear_0\left(\frac{\partial l_i}{\partial \pmb{a}}\frac{\partial \pmb{a}}{\partial \theta} + \frac{\partial l_i}{\partial \pmb{v}_\mathrm{rod}}\frac{\partial \pmb{v}_\mathrm{rod}}{\partial \theta}\right)\omega\space\space(t>>0)
\end{aligned}$$

計算の詳細：<velocity>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (none, fixed, affine)

　制御入力 $u_i$ が与えられたときの出力 $p_i$ は次の通りです。ここで、 $k_v$ は速度フィードバックゲイン（kv属性）です。

$$\begin{aligned}
p_i =& gain_0 \times u_i + bias_0 + l_i\space bias_1 + \dot{l_i}\space bias_2\\
=& k_v u_i - k_v\dot{l_i}
\end{aligned}$$

<velocity> & jointトランスミッション

　jointトランスミッションについて、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は上述の通りです。したがって、本組合せでの入出力関係は以下のようになります。

表 ジョイントのタイプと入力 $u_i$ - 出力 $p_i$ 関係

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。 　　 $p_i = k_v( u_i - gear_0\space\omega)$
"slide"	$x/v$ はそれぞれ関節変位/速度です。 　　 $p_i = k_v( u_i - gear_0\space v)$
"ball"	$\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度です。 　　 $p_i = k_v( u_i - |\pmb{gear}||\pmb{\omega}|)$
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。 　　 $p_i = k_v( u_i - \pmb{gear}\cdot \pmb{v})$

計算の詳細：<intvelocity>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (integrator, fixed, affine)

　制御入力 $u_{i,n}\space(n=0,1,...,t)$ が与えられてきたときの、時刻 $t+1$ における出力 $p_i$ は次の通りです。ここで、 $k_p$ は位置フィードバックゲイン（kp属性）、 $k_v$ はアクチュエータによる減衰（kv属性）です。

$$\begin{aligned}
p_i =& gain_0 \times \bigg(h\sum_{n=0}^{t}u_{i,n}\bigg) + bias_0 + l_i\space bias_1 + \dot{l_i}\space bias_2\\
=& k_ph\sum_{n=0}^{t}u_{i,n} - k_pl_i - k_v\dot{l_i}
\end{aligned}$$

活性化状態の更新式は $w_{i,t+1} = w_{i,t} + hu_{i,t}$ です。actearly属性が"true"の場合、上の $p_i$ の式は時刻 $t$ における出力の式となります（入出力間の遅延が1ステップ分減る）。

<intvelocity> & jointトランスミッション

　jointトランスミッションについて、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は上述の通りです。したがって、本組合せでの入出力関係は以下のようになります。ここで、以下の $p_i$ は時刻 $t$ （actearlyが"true"なら $t-1$ ）における出力となります。

表 ジョイントのタイプと入力 $u_i$ - 出力 $p_i$ 関係

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。 　　 $p_i = k_ph\sum_{n=0}^{t-1}u_{i,n} - gear_0(k_p\space\theta + k_v\space\omega)$
"slide"	$x/v$ はそれぞれ関節変位/速度です。 　　 $p_i = k_ph\sum_{n=0}^{t-1}u_{i,n} - gear_0(k_p\space x + k_v\space v)$
"ball"	$\theta/\pmb{n}=(x,y,z)$ はそれぞれ回転角/方向ベクトル（クォータニオン表現）です。また $\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度、 $\pmb{n_{gear}}$ は $\pmb{gear}$ の単位ベクトルです。 　　 $p_i = k_p h\sum_{n=0}^{t-1}u_{i,n} - |\pmb{gear}|\big(k_p(\pmb{n} \cdot \pmb{n_{gear}})\space \theta + k_v|\pmb{\omega}|\big)$ 　　（ $where\space \theta\in[-\pi,\pi]$ ）
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。 　　 $p_i = k_p h\sum_{n=0}^{t-1}u_{i,n} - k_v\space \pmb{gear}\cdot \pmb{v}$

計算の詳細：<damper>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (none, affine, none)

　以下は時刻 $t$ における制御出力 $p_i$ です。ここで、 $k_v$ は速度フィードバックゲイン（kv属性）です。

$$\begin{aligned}
p_i =& (gain_0 + l_i\space gain_1 + \dot{l_i}\space gain_2)\times u_i\\
=& -k_v\dot{l_i}u_i
\end{aligned}$$

<damper> & jointトランスミッション

　jointトランスミッションについて、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は上述の通りです。したがって、本組合せでの入出力関係は以下のようになります。

表 ジョイントのタイプと入力 $u_i$ - 出力 $p_i$ 関係

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。 　　 $p_i = -k_v( gear_0\space\omega)\space u_i$
"slide"	$x/v$ はそれぞれ関節変位/速度です。 　　 $p_i = -k_v(gear_0\space v)\space u_i$
"ball"	$\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度です。 　　 $p_i = -k_v|\pmb{gear}||\pmb{\omega}|\space u_i$
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。 　　 $p_i = -k_v(\pmb{gear}\cdot \pmb{v})\space u_i$

計算の詳細：<cylinder>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (filter, fixed, affine)

　制御入力 $u_{i,n}\space(n=0,1,...,t)$ が与えられてきたときの、時刻 $t+1$ における出力 $p_i$ です。ここで $A$ はシリンダの面積（area属性）、 $\tau$ は活性化ダイナミクスの時定数（timeconst属性）、 $b_j$ はbias属性のパラメタ $(j=0,1,2)$ です。diameter属性( $d$ )を指定した場合は、 $A:=\pi d^2/4$ として定義されます。

$$\begin{aligned}
p_i =& gain_0 \times \bigg(h\sum_{n=0}^{t-1}\Big(\frac{dyn_0-h}{dyn_0}\Big)^n u_{i,n}\bigg) + bias_0 + l_i\space bias_1 + \dot{l_i}\space bias_2\\
=& Ah \sum_{n=0}^{t-1}\Big(\frac{\tau-h}{\tau}\Big)^n u_{i,n} + b_0 + b_1l_i + b_2\dot{l_i}
\end{aligned}$$

活性化状態の更新式は $w_{i,t+1} = w_{i,t} + h(u_{i,t}-w_{i,t})/ dyn_0$ です。actearly属性が"true"の場合、上の $p_i$ の式は時刻 $t$ における出力の式となります（入出力間の遅延が1ステップ分減る）。

<cylinder> & jointトランスミッション

　jointトランスミッションについて、アクチュエータ長 $l_i$ および同速度 $\dot{l_i}$ は上述の通りです。したがって、本組合せでの入出力関係は以下のようになります。

表 ジョイントのタイプと入力 $u_i$ - 出力 $p_i$ 関係

タイプ	式
"hinge"	$\theta/\omega$ はそれぞれ関節角度/角速度です。 　　 $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 + gear_0(b_1\space\theta + b_2\space\omega)$
"slide"	$x/v$ はそれぞれ関節変位/速度です。 　　 $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 + gear_0(b_1\space x + b_2\space v)$
"ball"	$\theta/\pmb{n}=(x,y,z)$ はそれぞれ回転角/方向ベクトル（クォータニオン表現）です。また $\pmb{\omega} := (\omega_x,\omega_y,\omega_z)$ は関節角速度、 $\pmb{n_{gear}}$ は $\pmb{gear}$ の単位ベクトルです。 　　 $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 + |\pmb{gear}|\big(b_1(\pmb{n} \cdot \pmb{n_{gear}})\space \theta + b_2|\pmb{\omega}|\big)$ 　　（ $where\space \theta\in[-\pi,\pi]$ ）
"free"	$\pmb{gear}=:(x,y,z,r_x,r_y,r_z)$ はgear属性の値、 $\pmb{v} := (v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)$ はボディの速度（mjData.qvel[n:n+6]の値）です。 　　 $p_i = Ah \sum_{n=0}^{t-1}\big(\frac{\tau-h}{\tau}\big)^n u_{i,n} + b_0 - b_2\space \pmb{gear}\cdot \pmb{v}$

計算の詳細：<adhesion>の場合

【計算の詳細】

(dyntype, gaintype, biastype) = (none, fixed, none)

　以下は時刻 $t$ における制御出力 $p_i$ です。ここで、 $gain_0$ はアクチュエータのゲイン（gain属性）の第一要素です。

$$p_i = gain_0 \times u_i$$

muscle (MJCF/actuator)

概要 : muscle (MJCF/actuator)

　<muscle>は生物の筋を模したアクチュエータショートカットです。他のアクチュエータと比較してもかなり複雑ですが、最低限の筋機能を実現したい場合には以下のようなコードを書くだけでもOKです。<general>でも筋を作成することは可能ですが、<muslcle>を使用する方が便利だと思います。

<actuator>
    <muscle name="mymuscle" tendon="mytendon">
</actuator>

　通常、生物の筋肉は部位により大きく異なる振る舞いを見せますが、うまくスケーリングするとそれぞれ似た挙動を観察することができます。これを行うのがscale属性であり、既定では有効になっています。

この節はまだ記述が不十分なため、今後改稿予定です。他のアクチュエータに比べてもかなり機構が複雑なので…

属性 : muscle (MJCF/actuator)

図 固有の属性（<adhesion>）

属性	型:〈デフォルト値等〉 説明
timeconst	型：real(2)〈 "0.01 0.04" 〉 活性化/非活性化ダイナミクスの時定数 $\tau_\mathrm{act}, \tau_\mathrm{deact}$ です。
tausmooth	型：real〈 "0" 〉 上記 $\tau_\mathrm{act}$ と $\tau_\mathrm{deact}$ との間の、滑らかな移行の幅 $\tau_\mathrm{smooth}$ です。負でない必要があり、制御入力と同じ単位(?)です。
range	型：real(2)〈 "0.75 1.05" 〉 筋肉の動作長さの範囲 $r_\mathrm{min}, r_\mathrm{max}$ です（L0単位）。
force	型：real〈 "-1" 〉 静止時の最大有効力 $f$ です。この値が負の場合、筋の最大有効力は以下のscale属性を使用して決定されます。
scale	型：real〈 "200" 〉 force属性が負の場合、筋の最大有効力は、この値をmjModel.actuator_acc0で除算した値に設定されます。また、第２要素はqpos0のときにアクチュエータにかかる単位力により生じる、関節空間での角速度ベクトルのノルムです。言い換えれば、スケーリングにより、より多くの重量を引っ張る筋肉に対してより高い最大有効力が生成されます。
lmin	型：real〈 "0.5" 〉 正規化されたFLV（力-長さ-速度）カーブの下限です（L0単位）。
lmax	型：real〈 "1.6" 〉 正規化されたFLVカーブの上限です（L0単位）。
vmax	型：real〈 "1.5" 〉 筋力がゼロになる短縮速度です（L0/秒 単位）。
fpmax	型：real〈 "1.3" 〉 ピーク静止力を基準とした、 $l_\mathrm{max}$ で生成される受動的な力です。
fvmax	型：real〈 "1.2" 〉 ピーク静止力を基準とした、飽和伸長速度で生成される有効力です。

　<muscle>では、gainprm等のパラメタは以下のように設定されます。各変数の定義は上に従います。

種類	タイプ	値
活性化	"muslce"	dyntype="muslce" dynprm= $(\tau_\mathrm{act},\tau_\mathrm{deact},\tau_\mathrm{smooth})$
ゲイン	"muslce"	gaintype="muslce" gainprm= $(r_\mathrm{min},r_\mathrm{max},f,scale,l_\mathrm{min},l_\mathrm{max},v_\mathrm{max},f_\mathrm{p,min},f_\mathrm{v,max})$
バイアス	"muslce"	biastype="muslce" biasprm=gainprm

muscleのアクチュエータモデル

筋の長さと速度

　MuJoCoでは、トランスミッションの規定するアクチュエータ長 $l_i$ が、アクチュエータ全般に対し重要な役割を持ちます。これに加え、<muscle>ではその範囲（lengthrange）にも重要な役割が存在します。lengthrangeに関しては、lengthrange節も参照してください。

　通常、生体内では筋と腱が直列に接続され、「筋腱アクチュエータ」を形成します。これを、長さ $L_T$ が一定で非弾性な生物学的腱と、時刻により変化する長さ $L_M$ をもつ生物学的筋、とします。一方MuJoCoの筋-腱の関係性は少し異なります。空間特性（特に長さと速度）を持つ実体はあくまで腱であり、筋は腱を引っ張る抽象的な力生成のメカニズムにすぎません。このため、MuJoCoでの腱の長さは、生体における筋＋腱の長さに相当します。したがって、MuJoCoの腱の長さ（アクチュエータ長） $l_i$ は次のように書けます。

$$l_i = L_T + L_M$$

　長さに関してもう一つ重要な定数が筋の安静時長さ $L_0$ であり、筋が速度ゼロで最大の有効力を達成するときの長さ $L_M$ に等しい値です。これら $L_0,L_T$ の値をユーザが計算するのは難しいため、以下に説明する手順により自動的に算出されます。

1. 前述の計算によりlengthrange（以下 $[L_\mathrm{r,min},L_\mathrm{r,max}]$ ）が計算される
2. （未知の）定数 $L_0$ でスケールされた筋長 $L_M$ の動作範囲 $[r_\mathrm{min},r_\mathrm{max}]$ を参照する（range属性）
3. 以下の式に従い未知定数 $L_0,L_T$ を求める

$$\begin{aligned}
(L_\mathrm{r,min}-L_T)/L_0 &= r_\mathrm{min}\\
(L_\mathrm{r,max}-L_T)/L_0 &= r_\mathrm{max}
\end{aligned}$$

　このようにして求めた定数を使用し、実行時には筋長 $L$ と同速度 $V$ を以下のように計算します。

$$L = (l_i - L_T)/L_0,\space\space\space V = \dot{l_i}/L_0$$

参考文献

[1] MuJoCo XML Refernce

[2] MuJoCo Modeling

[3] MuJoCo Computation

[4] engine_forward.c

[5] engine_core_smooth.c