はじめに
現在私たちは様々な物理エンジンを使用することができます。強化学習などを見据えた際、おそらく最も初学者が選択しやすいのはBullet(PyBullet)でしょう。一方、論文などを読んでいるとMuJoCoやODEなどが頻繁に出てくるかと思います。
本記事では、5つの物理エンジンを比較した論文「Simulation tools for model-based robotics: Comparison of Bullet, Havok, MuJoCo, ODE and PhysX」の要約を行います。本記事は要約記事ですので、詳細(積分器の種類とか結果のグラフとか)は原論文を参照してください。この記事があなたの選択の一助になれば幸いです。
ODE : Open Dynamics Engine
TL;DR
- ロボットのシミュレーションにはMuJoCoが最適(次点はODE)
- 特にBulletと比較すると2~3倍ほど処理速度が違い、精度にも大きな差がある
- スイカゲームのようなシミュレーション(浮動体が多数)にはODEが最適
ただ初学者が始めやすいのはBullet(PyBullet)な気はします(特に強化学習向け)。PyBulletに比べMuJoCoなどはネット上に上がっている記事の量が少ないので…
【24/03/13追記】MuJoCoのチュートリアル記事を投稿しました!
背景と目的
複雑なロボットを(特に不確実な環境で)動作させるためには、ロボットへの移植前に行動方策のテストと検証を行う必要があります。近年は強化学習などにより特にこれが顕著ですが、このためには高速で正確な物理システムのシミュレーションを行う必要があります。
物理シミュレーションの手法の一つは再帰的アルゴリズムによるものであり、有名なものにSD/FASTやMATLAB Robotics Toolboxがあります。これらはなめらかな多関節ダイナミクスに重点が置かれた物理シミュレータですが、正確な接触ダイナミクスのシミュレーションを十分に行えるとは言えません。
近年はジョイント空間での効率的な処理(再帰的なアルゴリズム)に加えて、接触ダイナミクスをシミュレーションできるような新たなアプローチ(速度ステップ法)を組み合わせた物理エンジンも多く出てきています。当論文では、その中からMuJoCo、PhysX、Bullet、HavokおよびODEを用いて、それらの速度や精度、安定性の比較を行いました。
当該論文の筆者はMuJoCoエンジンの開発者です。このため、論文の副次的な目的はMuJoCoの長所と短所を明らかにすることともいえます。
方法・対象
当該論文ではMuJoCo, Physix, Bullet, HavokおよびODEの5物理エンジンを比較しました。各物理エンジンにより実装されている機能は異なるため、正確な比較のために共通機能のみを使用してモデルを作成しました。
- 関節
- ヒンジジョイントおよびフリージョイント(一切の固定がない)のみを使用
- 衝突判定
- 球体とカプセル(円柱+半球)、および固定の地面のみを衝突判定の対象として使用
- 接触
- 反発や転がり摩擦を除外(クーロン摩擦の基本的なもののみ)
- マルチボディダイナミクス
- ボディに作用する力を重力、ジョイントの拘束力と作動トルク、およびジョイントの剛性と減衰に限定
- ジョイントの摩擦などは不使用
【使用した物理エンジンの説明】
| 種類 | 説明 |
|---|---|
| ODE |
Open Dynamics Engine オープンソースの物理エンジンであり、ロボット工学関連で有名です。 |
| Bullet | オープンソースの物理エンジンです。PythonラッパーのPyBulletはネット上にドキュメントも多く初学者向けです。 |
| PhysX | Havokとともに最も広く使用されているゲームエンジンの一つです。物理的な精度の点での妥協も多く、例えばコリオリの力を考慮しません。このため、精度が重要なロボット工学シミュレーションには適しません。 |
| Havok | Havokも広く使用されているゲームエンジンであり、こちらも同様にコリオリの力を考慮しません。 |
| MuJoCo | オープンソースの物理エンジンであり、多関節ロボットのシミュレーションに焦点を当てています。 |
当該論文では、あらゆるモデルシステムに適用できる普遍的なテスト・パフォーマンス指標として、以下の4項目を提案しています。一般的なロボットシステムへの応用可能性を鑑み普遍的な指標を提案しているため、後者2つに関しては補助的な指標です。これは(特に)エネルギー・運動量保存に関して、一般的なロボットシステムがこれを保持しないことも多いためです。該当する場合にのみ比較に使用してください。
| 指標 | 説明 |
|---|---|
| 一貫性 | タイムステップが極小のときを基準とし、大きくした場合の偏差(数値積分誤差)を見ます。 |
| 速度-精度のトレードオフ | どれだけ高速かつ高精度に計算できるかを見ます。 |
| (エネルギー・運動量保存) | どれだけ正確に保存されるかを見ます。 |
| (把持安定性) | 簡易PD制御を用いた把持の安定性(何秒把持できるか)を見ます。同じテスト環境であっても、現実に比べシミュレーションでは難しいようです。 |
安定性(爆発しないこと)も指標として考えられます。特にゲーム向けの物理エンジンではこちらを重要視しており、一貫性を捨てる代わりに安定性を向上させるように最適化されているようです
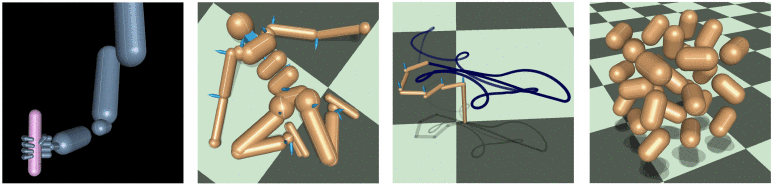
使用したモデルは以下の通りです。腕・人体・チェーンはロボットシステム的シミュレーションの検証を行い、27カプセルはゲームシステム的シミュレーションの検証を行います。
図 使用されたモデル[1](左)腕(中左)人体(中右)チェーン(右)27カプセル
【モデル詳細】
| モデル | 自由度 | 説明 |
|---|---|---|
| 腕 | $35$ | Shadow Handをもとにした上肢のモデルです。固定ばねダンパによりカプセルの把持をシミュレートします。ばね・ダンパのパラメタはそれぞれ $K=0.4\space\mathrm{Nm/rad}$ と $B=0.005\space\mathrm{Nms/rad}$ です。 目的:把持の安定性(多くの同時接触を伴うため、動的シミュレーションは困難)の検証 |
| 人体 | $25$ | 立位から床に倒れるまでのシミュレーションを行います。各関節には正弦波開ループトルクがかかります。 上肢6DOF(肘×2+肩×4)、腰3DOF、下肢8DOF(股×4+膝×2+足首×4)、本体6DOF 目的:速度と精度のトレードオフの測定 |
| チェーン | $5$ | 5つのボディと5つのヒンジジョイントからなります。ボディはそれぞれ互いに衝突しない高さに位置します。 ゼロ以外の初速度がジョイントに与えられ、シミュレーションでは受動的に各ボディが動作します。 目的:一貫性などの検証 |
| 27カプセル (フリーボディ) |
$162$ ( $27\times 6$ ) |
ランダムな位置と姿勢で配置された27個のカプセルが床に落とされるモデルです。 目的:ロボティクスには直接関係しませんが、ゲームエンジンが最適化されている種類のシミュレーションを示すために使用します。 |
フリージョイント:ほかの物体との間に位置・姿勢関係の制約を持たない物体のことです。手から離れた物体などがそうであり、6の自由度を持ちます。
フリージョイント含め、上記モデルのすべてのジョイントに摩擦は設定されていません。
シミュレーション環境 : Windows 8.1(i7-3930K)
結果
各モデルのシミュレーション結果を以下に示します。以下の指標はすべて「計算速度 [ kHz ]」であり、1秒当たりに可能なシミュレーションの回数を1000回のシミュレーションにより求めたものです。このため数値が大きいほど速いことを示します。
表 各モデルシミュレーションの計算速度[kHz].MuJoCoは数値積分にEulerを使用しています。またチェーンモデルのBulletの結果はBulletMBと呼ばれる、多関節ロボット解析向けのBulletの結果を示しています。
| Bullet | Havok | MuJoCo | ODE | PhysX | |
|---|---|---|---|---|---|
| 腕 | 2.9 | 3.7 | 6.5 | 6 | 3 |
| 人体 | 4.8 | 5 | 14.5 | 9.1 | 3.8 |
| チェーン | 81.4 | 23.8 | 243.2 | 36 | 6.4 |
| 27カプセル | 4.4 | 6.2 | 3.6 | 23.7 | 5.2 |
実験の結果を以下に示します。
- 計算速度
- ロボットシステムに関するシミュレーションではMuJoCoが最も速い(腕、人体、チェーン)
- ゲームシステムに関するシミュレーションではODEが最も速い(27カプセル)
- 一貫性
- MuJoCoはすべてのシミュレーションにおいて一貫性が高かった
- ゲーム向けのエンジン(Havok, PhysX)は一貫性が低かった
- 把持の安定性
- MuJoCoおよびPhysXはうまく把持することができた
- タイムステップを大きくするほど安定性が下がった
- エネルギー・運動量保存
- ODEが保存則をもっともよくシミュレートした(特に角運動量)
- MuJoCoはジョイント座標系を使用するため線形運動量保存において不利(ほかはデカルト座標系)
結論
論文ではシミュレータ性能の速度精度尺度を導入し、比較したエンジンは、どれも一様に他のエンジンより優れているわけではないことを示しました。この尺度は解析的ベンチマークが利用できない複雑なシステムに適用可能であるので、特にロボティクスを目的とした際の物理エンジンの選択に役立ちます。
MuJoCoは、ロボット工学に関連する制約のあるシステムにおいて、最も速く、最も正確であり、より大きな時間ステップで安定した把持が可能でした。すなわち、ロボティクス関連のモデル(基本的に自由度の低いジョイントからなり、フリージョイントをほとんど持たないようなもの)にはMuJoCoが適しているといえます。
一方、多数の切り離された物体からなるモデルではMuJoCoが最も遅く、ODEが最も高速でした。また、エネルギー・運動量保存などもMuJoCoは苦手なようです。
参考文献
[1] T. Erez, Y. Tassa and E. Todorov, "Simulation tools for model-based robotics: Comparison of Bullet, Havok, MuJoCo, ODE and PhysX," 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 2015, pp. 4397-4404, doi: 10.1109/ICRA.2015.7139807. keywords: {Engines;Joints;Accuracy;Computational modeling;Robot kinematics;Mathematical model},