【GAS】緯度経度から２点間の距離を求める

##概要
仕事で距離を知りたいことが多く、いつもGoogleMapの「距離を測定」で測っていたけれど、これってもしかして計算できるのでは？と思いググったところ、出るわ出るわ緯度経度から２点間の距離を求める方法。

地球を楕円体として見たとして、いくつかの定数が分かればヒュベニの公式ってので求まるらしい・・・。

##続編あり
「測地線航海算法」で、より高精度に距離を求める続編あり。
Qiita記事：緯度経度からの距離計算 ヒュベニより航海算法の方が高精度説

この記事での問題点なども解決^^)b 閑話休題

##取りあえず結論＆コード
色々あって、２点の緯度と経度を入れたら距離[km]を計算することに成功！問題や疑問は残ったけども、取りあえず自分の仕事で使うには実用レベルの物が完成。

スプレッドシートのセル上で、次のように距離を求められるようにした。
=関数(緯度A, 経度A, 緯度B, 経度B)

理屈やら検討は後回しにして「コード.gs」がコチラ。

function measureDistance(latA,lngA,latB,lngB){ 
   
  //定数定義 
  const a = 6377397.16;             //長半径a(m) 
  const b = 6356079;                //短半径b(m) 
  const E2 = 0.006674361028297;     //第一離心率eの二乗 
  const M_numer = 6334832.10663254; //子午線曲率半径Mの分子a(1-e^2) 
   
  //緯度経度をラジアンに変換 
  var latARad = latA * (Math.PI/180); 
  var lngARad = lngA * (Math.PI/180); 
  var latBRad = latB * (Math.PI/180); 
  var lngBRad = lngB * (Math.PI/180); 
   
  //緯度経度の差 
  var dy = latARad - latBRad; 
  var dx = lngARad - lngBRad; 
   
  //緯度の平均値 
  var latAve = (latARad + latBRad) / 2; 
   
  //子午線曲率半径M 
  var sinP = (Math.cos(latAve)); 
  var sinP2 = sinP * sinP; 
  var W_ofroot = 1 - (E2 * sinP2); 
  var W = (Math.sqrt(W_ofroot)); 
  var W3 = W*W*W; 
  var M = M_numer / W3; 
   
  //卯酉線曲率半径N 
  var N = a / W; 
   
  //途中式
  var f1 = dy*dy*M*M; 
  var f2 = dx*N*(Math.cos(latAve)); 
  var f3 = f2 * f2; 
  var f4 = f1 + f3; 
   
  //2点間の距離（ｍ→ｋｍ）
  var D = (Math.sqrt(f4)); 
  var km = D / 1000; 
   
  return km; 
   
}

##理屈＆いいわけ
公式などの詳しい解説は専門的なサイトが多いので割愛。

最初に定義している各定数について、測定した時期や団体？などによって違いがある模様。３種類ほど試して、GoogleMapの距離測定との誤差が一番小さかった「ベッセル楕円体（旧日本測地系）」と呼ばれる物を使用。

途中の式はスッキリさせたいけど・・・これ以上まとめると計算結果が狂うのでこんな感じに^^;　この辺が素人リーマンの限界か？

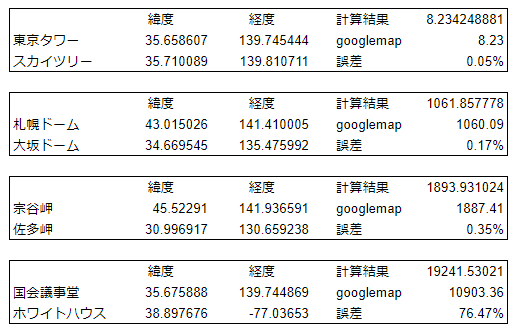
##実際に計算してみた
緯度経度は、GoogleMapの「この場所について」で取得。

負の値があるからか、国会議事堂からホワイトハウスまでの距離で酷い誤差が出てしまった。それ以外は悪くなくて、東京タワーからスカイツリーなんて実質誤差ゼロ！個人的には東京都内でしか使わないので問題無さそう ^^)b

距離が延びるほど誤差が大きくなるなら、緯度経度の平均を中間として、それぞれから中間までの距離を計算して足せば良いでは？と思ったけど、さらに誤差が大きくなりましたとさ（笑）

楕円体のカーブが原因かも？GoogleMapAPIの距離計算は地球を球体として計算しているとの記述もあったので、楕円体として計算しているヒュベニの公式と誤差が出る？

##？だらけになったけど
限られた範囲（と言っても生活圏的には十分）で使える距離測定関数が完成。

余談ですが、エクセルでも計算できました。

###おしまい