動的計画法(DP)勉強メモ

ちょっと調べたのでまとめてみます。

動的計画法(DP)とは？

まず、Wikipediaを見てみる。(引用は一部改変しています)

細かくアルゴリズムが定義されているわけではなく、下記2条件を満たすアルゴリズムの総称である。
1. 分割統治法：部分問題を解き、その結果を利用して、問題全体を解く
2. メモ化：部分問題の計算結果を再利用する

ふむ、分けること、メモ化すること、の２つを含むアルゴリズムであると。
適用するには条件があるそうな。

最適化問題に適用する場合、一般的に、以下の2つが適用する問題に成立していないといけない。
1. 部分構造最適性や最適性原理
2. 部分問題重複性

部分構造最適性

部分構造最適性とは、以下の2条件が成立していることをさす。
ⅰ. 部分問題も同じ最適化問題が成立している
ⅱ. 部分問題間が独立している

何やら漢字だらけで難しそうだが、ⅰはこんな感じだと思う。


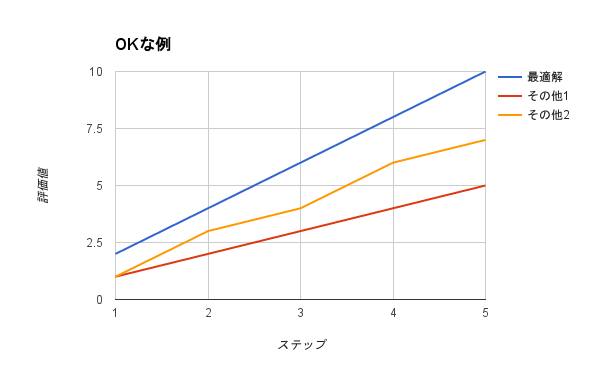
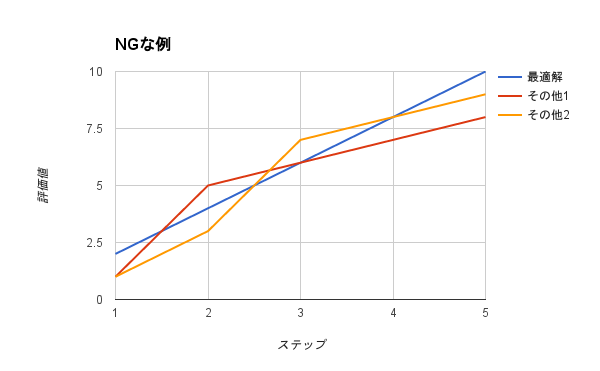
例えば問題を5つのステップに分割して解くとする。その際、各ステップでの最適解が、全体の最適解と一致しなければならない。NGな例の、ステップ2ではその他1(赤)、ステップ3ではその他2(黄色)が最適解だが、全体の最適解ではない。こういった性質の問題は動的計画法では解けない。

ⅱは大体そうなんじゃないかって気がするけど。。。NGな例って何があるんだろう？

部分問題重複性

部分問題重複性とは、同一の部分問題が繰り返し出現することである。

これがないとメモ化する意味がなくなってしまう、ということかな。

例題(フィボナッチ数列)

ボトムアップ方式とトップダウン方式それぞれ疑似コードが載っている。もうこれは見たとおり。再帰よりはループのほうが処理を思い浮かべやすい、と思った。

動的計画法といえば、な例題

ナップサックですよね。今度はこちらを見ます。
フィボナッチ数列はメモ化のテーブルが1次元(何番目か)だったが、ナップサック問題は2次元(残りの品物*ナップサックの容量)になるのでちょっと複雑。でもやることは、問題を分割して部分解でテーブルを埋めていくのみ。
ちょっと問題が大きいので小さくする。ナップサックの容量5kg、品物は以下の4つとする。

ID	重さ(kg)	価値
0	1	3
1	2	2
2	2	1
3	1	2

今回埋めるべきテーブルは下のような感じ。求めるべきは、残り品物4、ナップサック容量5kgの場合、テーブルで言うと一番右上(0, 5)。

↓品物/→容量	0	1	2	3	4	5
0	-	-	-	-	-	求めたいのはここ
1	-	-	-	-	-	-
2	-	-	-	-	-	-
3	-	-	-	-	-	まずここ

最初に手を付けるのは一番右下(3, 5)、それから徐々に上に向かってテーブルを埋めていく。
(3, 5)ではナップサックの容量5で、品物3を入れるか入れないか決める。入れたほうが価値は大きくなるので、(3, 5)は2と決まる。

↓品物/→容量	0	1	2	3	4	5
0	-	-	-	-	-	求めたいのはここ
1	-	-	-	-	-	-
2	-	-	-	-	-	次はここ
3	-	-	-	ここが必要	-	2

次に(2, 5)を求める。そのためには、(3, 5)と(3, 3)が必要になる。(3, 5)は品物2を入れなかったパターン、(3, 3)は入れたパターン。(3, 5)は先程求めた2である。(3, 3)は(3, 5)と同様に2になる。(2, 5)は(3, 5)か(3, 3)に品物2の価値を足したものの大きい方なので、3と決まる。

↓品物/→容量	0	1	2	3	4	5
0	-	-	-	-	-	求めたいのはここ
1	-	-	-	-	-	-
2	-	-	-	-	-	3
3	-	-	-	2	-	2

同じように、(1, 5), (0, 5)と求めることで、最終的に求めたい解が得られる。

文章にすると超絶わかりにくいが、実際テーブルを手で埋めていくと理解できる。この例だと微妙だが、一応メモ化も効いていることがわかる。
この手順をプログラムにすると、上で挙げたこちらのプログラムになる。
なるほどー

問題探してみた

これが易しくていい感じだった。テーブルは1次元。

おわりに

プロコンやる上で必ずといっていいほどこやつが出てくるので、しっかり抑えたいと思い記事にしてみた。結局は演習数こなすしかないと思うけど。がんばろう。