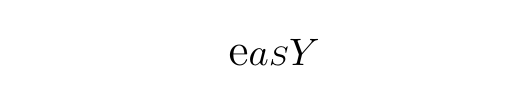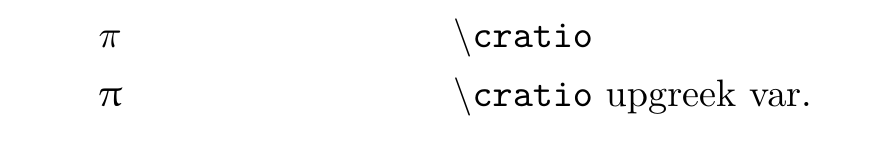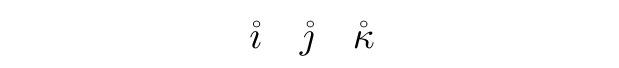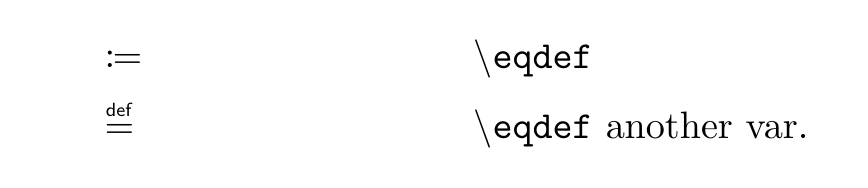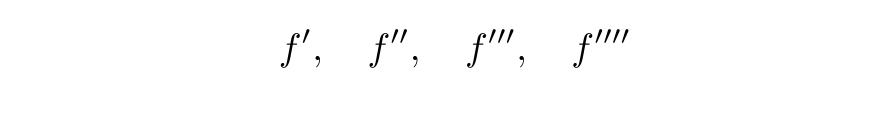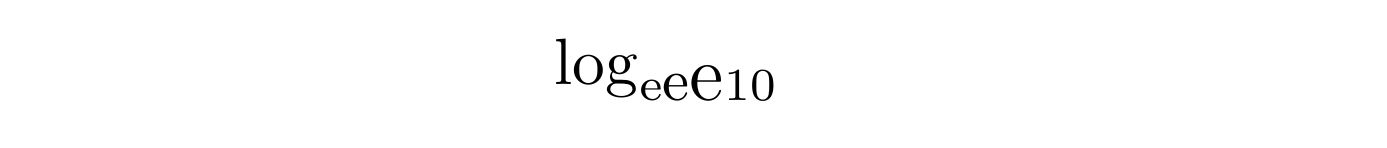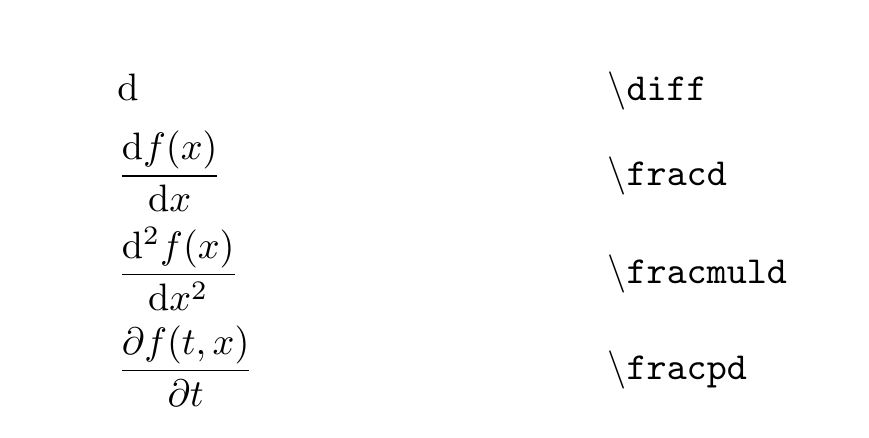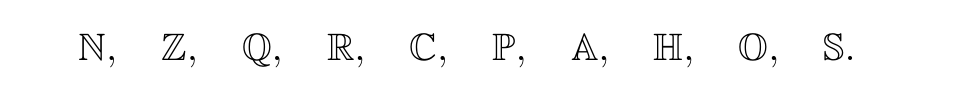LaTeX で定義として管理しておいた方が良い数式コマンド

$\rm\LaTeX$ で数式を打っていると，先に定義しておいた方が便利な言葉や表記方法に議論の余地があるためにさまざまな表記が存在するものがある．
これらは新たなコマンドとして定義しておき，のちにコマンドを変更することで対応した方が非常に賢明である．

多くのコマンドを覚えることを避けつつも，さまざまな文書で統一したコマンドで打つことが出来るようになる．
出力結果を変更したければ，定義を変えてしまえばいい．

もし，この記事のコマンド定義を使いたい人へ
新たなコマンドのネーミングセンスが悪い場合があります．好きに変更してください．記事最下で紹介した定義をまとめています．

本記事では，amsmath パッケージを使うことを標準としています

コマンドの定義方法

コマンドの定義方法はいくつかあるが，今回は主に\newcommand を使用する．
すでに定義済みのコマンドに対しては\renewcommand を使用すればいいが，どのコマンドが使用不可になるのかを理解している必要があるため，少々面倒なことになる可能性もある．なるべく避けておきたい．

次のように定義しておきたい．

\newcommand{<NEW command>}[<argument>]{%
    <DIFFINE command>    %
}

また，* 付きの\newcommand* は定義されたコマンドの改行を許可しない定義方法になる．
今回はほとんど使用しない．

複数行に渡って定義を書いているのは，定義されているコマンドの内容がどのようになっているのか理解しやすくするためと別の表式に変更する際に% で切り替えられるようにするためである．

\newcommand{<NEW command name>}[<argument>]{%
%    <OLD diffine command>    % このコマンドは使用せずに下に新たに定義しなおす
    <NEW diffine command>    %
}

もちろん，まったく変更する予定のない場合には1行で書いてしまっても良い．

より発展的な定義方法を望む場合にはxparse パッケージ¹を利用すると良いだろう．このパッケージは，\newcommand では定義することのできないオプション等を付与することが出来る．

xparse パッケージを利用しないがオプションのような定義をしたい場合は，<argument> を使ってごまかしておこう．
オプション不要の場合であっても必ず{} を付けなければならないのが面倒ではあるが......

!!新たに定義する際の注意点

いくつかの注意点があるので，列挙しておきたい．

• \def, \let などのコマンドを使用せずに\newcommand, \renewcommand を使用する
• 既に定義されているコマンド名を極力利用しない
• 自作したコマンドで新たにコマンドを定義しない
• 多くのパッケージに依存したコマンドを定義しない
• コマンド名を極端に短くすることは避ける

パッケージの更新や自作コマンドの変更によって，変わってしまうことをなるべく避けるように心掛けたい．

良くない例 :
発散を意味するdiv をコマンドとして定義したい．
以下のように定義してみる．

\newcommand{\div}{%
    \mathrm{div}    % 
}

このように定義したとき，\div はすでに÷ として定義されているので使用することが出来ない．
また，\renewcommand として上書き定義することも出来るが，このようにした場合には元の÷ を出す方法がなくなる．

ちなみに，divergence は\DeclarMathOperator で定義した方がよい．

\DclarMathCommand{\divergence}{div}

amsmath で提供されている\sin 等と同等の表示となる．
このように，\newcommand で定義するよりもパッケージから提供されているコマンドを用いたほうが良い場合もある．

○ 定数値

定数値は立体(ローマン体)で書くべきだと言う主張は根強い．
無次元量の定数値に関してはローマン体で書き，次元のある量はイタリック体で書くようだ．

以下にはよく使われるネイピア数と円周率についてあげておいた．

■ ネイピア数

ローマン体にすべきだろうが，同じサイズでは\text で出したe なのか分からない．\mathsf を用いてサンセリフ体にするのも少し奇妙だ．
ちょっとだけ大きくして強調しておこう．

\newcommand{\napier}{%
%    \mathrm{e}    % 
    \mathnormal{\mbox{\large{$\mathrm{e}$}}}    % 
}

これで，おおよそ\scriptstyle のアルファベット大文字と同程度の大きさになっている．

\napier a {\scriptstyle S} Y

正直に言えば，ネイピア数というよりはe の肩に乗せる書き方だと思えば，\exps と名づけた方が明解かもしれない．

\newcommand{\exps}[1]{% exponential of superscript
%    \mathrm{e}^{#1}    % 
    \mathnormal{\mbox{\large{$\mathrm{e}$}}}^{#1}    % 
}

■ 円周率

\pi は運動量として扱う場合もある．

小文字ギリシャ文字はさまざまなフォントの変更に対応していない．したがって，同一の記号を用いるほかないだろう．
しかし，テキスト内で円周率であるかどうかを見分けるためにも，新たなコマンドとして定義しておいても良いだろう．

\newcommand{\cratio}{% circle ratio 
    \pi    % 
}

upgreek パッケージを導入すれば，\uppi を利用することが出来る．

\RequirePackage{upgreek}
\newcommand{\cratio}{%
    \uppi    % 
}

○ 虚数単位

虚数単位はローマン体にするべきなどさまざまな意見がある．しかし，個人的にはローマン体では少し都合が悪いように見える．
イタリック体で虚数単位にしてみたい．

\newcommand{\imaginaryi}{% imaginary i
%    \mathrm{i}    % 
    \mathring{\imath}    % 
}
\newcommand{\imaginaryj}{% imaginary j
%    \mathrm{j}    % 
    \mathring{\jmath}    % 
}

ちなみに，四元数まで対応しようとするとk が必要になるが，どうしようか．

\newcommand{\imaginaryk}{% imaginary k
%    \mathrm{k}    % 
    \mathring{\kappa}    %
}

これは少々強引すぎるかもしれない．

四元数を取り扱うのであれば，文脈からある程度i, j, k が虚数単位に相当していることは明らかであり，その他の部分で同じ文字を使用しないようにすれば良いように思われる．

ここで，正直に\mathrm でローマン体にしておいた方が楽なのかもしれないと思い知らされている気がする．

○ 定義イコール

何らかの定義をする際には:= や合同記号を用いたりするだろう．
これらは特に気にせずに\equiv や\coloneqq を使用すればいいだろう．

\newcommand{\eqdef}{%
    \coloneqq    % 
}

場合によっては以下のように変更する可能性もあるだろう．

\stackrel{\scriptscriptstyle \mathsf{def}}{=}

○ アクセント記号

$\rm\LaTeX$ では標準的なアクセントがいくつかある．また，amsmath でもアクセントが追加されている．

これらには追加されていないアクセントをいくつか定義しておきたい．

\newcommand{\dash}[1]{%
    #1 ^\prime    % 
}
\newcommand{\ddash}[1]{%
    #1 ^{\prime\prime}    %
}
\newcommand{\dddash}[1]{%
    #1 ^{\prime\prime\prime}    %
}
\newcommand{\ddddash}[1]{%
    #1 ^{\prime\prime\prime\prime}    %
}

時間微分に\dot 等を利用しているのに．空間微分で\dash がないのはどうしてなのか不思議だ．\ddddot まであるので，\ddddash まで定義しておいた．

\dash{f},\quad \ddash{f},\quad \dddash{f},\quad \ddddash{f}

高階微分に対しても対応しておいた方が良いだろうか．

\newcommand{\hodash}[2]{% High order dash
    #2 ^{(#1)}    % 
}

\hodash{10}{f}

xparse パッケージを利用して作成する場合には，\dash のオプションでn 等を入れることでいくつかの\prime や(n) を挿入できるようなコマンドを作成すると良いだろう．

○ 対数

数学的に使われていれば自然対数，数値解析などで使われていれば常用対数であるなど，ある程度の棲み分けがされているがどちらかハッキリとしない状況もある．テキスト内では明示的に書いておいて，出力結果には反映させないようにしても問題ないように思われる．

ここではあえて対数の底があからさまになるようにしている．
また，自然対数に関して，e が\scriptstyle となっているので非常に小さく見える．10 と同じサイズくらいにしておいた方が自然なのではないかと思う．

いくつかサンプルとして\log に続く下付き文字を並べておく．

\log_{
    \mathrm{e}    % もっとも小さい
    \mathnormal{\mbox{\small$\mathrm{e}$}}    % これがもっとも10に近い大きさ
    \mathnormal{\mbox{\large$\mathrm{e}$}}    % 少し大きすぎる
    10    % これと同じくらいの大きさにしたい
}

ちなみに，大文字アルファベットの\scriptstyle は小文字アルファベットと同じくらいの高さになるので，この場合ではe が\log のo と同じくらいのサイズになることに注意したい．(これを嫌う人もいるだろう)

\newcommand{\nlog}{% Natural logarithm
%    \log_{\mathrm{e}}    % 
    \log_{\mathnormal{\mbox{\small$\mathrm{e}$}}}    % 個人的にはこちらの方が好みである
}
\newcommand{\clog}{% Common logarithm
    \log_{10}    % 
}

これの発展として任意の対数の底を付与した状態でコマンドを定義する場合，\2log や\log2 などでは定義できないことに注意しておきたい．

○ 差分

微積分を表す際には，d を用いる．これを立体にするかどうかは非常に興味のある部分だ．

\newcommand{\diff}{% differential
    \mathrm{d}    % 
}

これに伴って，微分形式である場合にも\mathrm{d} で表記しておきたい．
分数ごと定義してしまおう．

\newcommand{\fracd}[2]{% fraction of differential
    \genfrac{}{}{}{}{\mathrm{d} #1}{\mathrm{d} #2}    % 
}
\newcommand{\fracmuld}[3]{% fraction of multi differential
    \genfrac{}{}{}{}{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}    % 
}% xperse パッケージを利用して，オプションで追加できるようにした方が賢い

偏微分に関しても以下のように定義しておけば容易になるだろう．

\newcommand{\fracpd}[2]{% fraction of partial differential
    \genfrac{}{}{}{}{\partial #1}{\partial #2}    % 
}

○ 転置行列

さまざまな流派によって表記方法が変化するため，新たに定義しておいた方が賢明だろう．

\newcommand{\transpose}[1]{%
%    {\vphantom{#1}}^{t}\! #1    % 左上に"t" の場合
    #1 ^\mathsf{T}    % 右上に"T" の場合
}

以下の記事でも紹介している．ぜひ参考にしてもらいたい．

行列環境のエトセトラをまとめる#-転置行列 - Qiita

○ ベクトル表記

矢印にするのか，太字にするのか等さまざまなベクトル表記があるが，$\rm\LaTeX$ を作成する際にいちいちコマンドを使い分けていては面倒であり，かと言って，1つのドキュメント内でベクトル表記を変えるということもあまりない．

\newcommand{\vect}[1]{%
    \overset{\scriptscriptstyle{\boldsymbol{\to}}}{\boldsymbol{#1}}    % ボールドかつ矢印付き
}

以下の記事でより詳しく紹介している．ぜひ参考にしてもらいたい．

ベクトル書きたい - Qiita

○ イプシロン記号

イプシロンを用いたエディントンのイプシロン記号やレヴィ=チヴィタ記号と呼ばれる記号も定義しておきたい．テンソルを扱うときに出てきたりする．

\epsilon と\varepsilon の2つの表記方法がある．また，epsilon と打つのが面倒くさい．

\newcommand{\levi}{% Levi-Civita symbol
%    \epsilon    % 
    \varepsilon    % こちらの方がよく使用される気がする
}

添え字は上付きも下付きも使用するので，イプシロンの書き方を再定義しただけに終わっている．

○ 代数

代数学では黒板太字(Blackboard bold)を使って整数や複素数などを表したりする．
amssymb パッケージから提供されている\mathbb を利用して定義しておこう．

\RequirePackage{amssymb}
\newcommand{\bbN}{% 
    \mathbb{N}    % natural number/ 自然数
}
\newcommand{\bbZ}{% 
    \mathbb{Z}    % zahlen/ 整数
}
\newcommand{\bbQ}{% 
    \mathbb{Q}    % quotient/ 有理数
}
\newcommand{\bbR}{% 
    \mathbb{R}    % real number/ 実数
}
\newcommand{\bbC}{% 
    \mathbb{C}    % complex number/ 複素数
}
\newcommand{\bbP}{%
    \mathbb{P}    % prime number/ 素数
}
\newcommand{\bbA}{%
    \mathbb{A}    % algebraic number/ 代数的数
}
\newcommand{\bbH}{%
    \mathbb{H}    % hamilton number/ 四元数
}
\newcommand{\bbO}{%
    \mathbb{O}    % octonion/ 八元数
}
\newcommand{\bbS}{%
    \mathbb{S}    % sedenion/ 十六元数
}

\bbN,\quad \bbZ,\quad \bbQ,\quad \bbR,\quad \bbC,\quad \bbP,\quad \bbA,\quad \bbH,\quad \bbO,\quad \bbS.

これ以外にも定義したい場合には同様に定義しておけば良いだろう．
\N と定義しても問題ないが安易な定義は競合しやすくなるので，頭にbb を付与しておいた．

○ ラグランジアンとか

ラグランジアンやハミルトニアンのように何度も使用するようなシンボルも定義しておきたい．\mathcal{L} と何度も打っているのも面倒である．

\RequirePackage{mathrsfs}
\newcommand{\lagr}{% Lagrangian
    \marhcal{L}    % 
}
\newcommand{\lagrd}{% Lagrangian density
    \mathscr{L}    % need "mathrsfs" package
}
\newcommand{\hamil}{% Hamiltonian
    \mathcal{H}    % 
}
\newcommand{\hamild}{% Hamiltonian density
    \mathscr{H}    % need "mathrsfs" package
}

意味が明瞭であれば，\L や\Ld, \H, \Hd 等と定義しておいても良いだろう．

○ よく使用されるフレーズ

数式中に入る言葉には以下の2つのコマンドを使用するが，使いどころが若干異なる．なるべく気にしておいた方が良いかもしれない．

コマンド	使いどころ	スペース
\mathrm	関数名，数式省略	無効
\text	数式の説明，注釈	有効

■ 左辺・右辺

\newcommand{\lhs}{% 左辺
    \mathrm{(LHS)}    %
}
\newcommand{\rhs}{% 右辺
    \mathrm{(RHS)}    %
}

■ 定数

\newcommand{\const}{%
    \mathrm{const}    % 
}

■ 有限値

\newcommand{\finite}{%
    \mathrm{finite}    % 
}

■ 複素共役

\newcommand{\hc}{%
    \mathrm{h.c.}    % 
}

■ 人名

関数に人名を付与する場合がある．頻繁に登場する場合，非常に面倒である．
これに関しては適宜定義しておきたい．

\newcommand{<command name>}{%
    \mathrm{<personal name>}    % 
}

また，"crit" や"in", "out" 等もよく登場する．同様に定義しておくと良いだろう．

これと同時に，これらが常に付与されるような変数についても一括で1つのコマンドとして定義しておくと楽に作成することが出来るようになる場合がある．適宜定義しておきたい．

○ オーダー

\newcommand{\order}[1]{%
    \mathcal{O} \! \left( #1 \right)    % 
}

☆ まとめ

以上で紹介したコマンドの定義をそのまま列挙して貼り付けておきます．
コピペしたい方はそのままどうぞ．

定義しておきたいコマンドまとめ (折りたたみ)

プリアンブルにそのまま入れるか，math-command.tex などとしたファイルを\input して利用すれば良いだろう．

% 
\RequirePackage{amsmath}
\RequirePackage{amssymb}
\RequirePackage{mathrsfs}
\RequirePackage{upgreek}
\RequirePackage{bm}

%% ネイピア数
\newcommand{\napier}{%
%    \mathrm{e}    % 
    \mathnormal{\mbox{\large{$\mathrm{e}$}}}    % 
}
\newcommand{\exps}[1]{% exponential of superscript
%    \mathrm{e}^{#1}    % 
    \mathnormal{\mbox{\large{$\mathrm{e}$}}}^{#1}    % 
}

%% 円周率
\newcommand{\cratio}{% circle ratio 
    \pi    % 
%    \uppi    % need "upgreek" package
}

%% 虚数単位
\newcommand{\imaginaryi}{% imaginary i
%    \mathrm{i}    % 
    \mathring{\imath}    % 
}
\newcommand{\imaginaryj}{% imaginary j
%    \mathrm{j}    % 
    \mathring{\jmath}    % 
}
\newcommand{\imaginaryk}{% imaginary k
%    \mathrm{k}    % 
    \mathring{\kappa}    %
}

%% 定義イコール
\newcommand{\eqdef}{%
    \coloneqq    % 
%    \stackrel{\scriptscriptstyle \mathsf{def}}{=}
}

%% 対数
\newcommand{\nlog}{% Natural logarithm
%    \log_{\mathrm{e}}    % 
    \log_{\mathnormal{\mbox{\small$\mathrm{e}$}}}    % 
}
\newcommand{\clog}{% Common logarithm
    \log_{10}    % 
}

%% 差分/微分
\newcommand{\diff}{% differential
    \mathrm{d}    % 
}
\newcommand{\fracd}[2]{% fraction of differential
    \genfrac{}{}{}{}{\mathrm{d} #1}{\mathrm{d} #2}    % 
}
\newcommand{\fracmuld}[3]{% fraction of multi differential
    \genfrac{}{}{}{}{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}    % 
}
\newcommand{\fracpd}[2]{% fraction of partial differential
    \genfrac{}{}{}{}{\partial #1}{\partial #2}    % 
}

%% アクセント記号
\newcommand{\dash}[1]{%
    #1 ^\prime    % 
}
\newcommand{\ddash}[1]{%
    #1 ^{\prime\prime}    %
}
\newcommand{\dddash}[1]{%
    #1 ^{\prime\prime\prime}    %
}
\newcommand{\ddddash}[1]{%
    #1 ^{\prime\prime\prime\prime}    %
}
\newcommand{\hodash}[2]{% High order dash
    #2 ^{(#1)}    % 
}

%% 転置行列
\newcommand{\transpose}[1]{%
%    {\vphantom{#1}}^{t}\! #1    % 左上に"t" の場合
    #1 ^\mathsf{T}    % 右上に"T" の場合
}

%% ベクトル表記
\newcommand{\vect}[1]{%
    \overset{\scriptscriptstyle{\boldsymbol{\to}}}{\boldsymbol{#1}}    % 
%    \bm{\vec{#1}}    % need "bm" package
%    \overset{\boldsymbol{\to}}{\boldsymbol{#1}}    % 
}

%% レヴィ=チヴィタ記号
\newcommand{\levi}{% Levi-Civita symbol
%    \epsilon    % 
    \varepsilon    %
}

%% 代数    need "amssymb" package
\newcommand{\bbN}{% 
    \mathbb{N}    % natural number/ 自然数
}
\newcommand{\bbZ}{% 
    \mathbb{Z}    % zahlen/ 整数
}
\newcommand{\bbQ}{% 
    \mathbb{Q}    % quotient/ 有理数
}
\newcommand{\bbR}{% 
    \mathbb{R}    % real number/ 実数
}
\newcommand{\bbC}{% 
    \mathbb{C}    % complex number/ 複素数
}
\newcommand{\bbP}{%
    \mathbb{P}    % prime number/ 素数
}
\newcommand{\bbA}{%
    \mathbb{A}    % algebraic number/ 代数的数
}
\newcommand{\bbH}{%
    \mathbb{H}    % hamilton number/ 四元数
}
\newcommand{\bbO}{%
    \mathbb{O}    % octonion/ 八元数
}
\newcommand{\bbS}{%
    \mathbb{S}    % sedenion/ 十六元数
}

%% フレーズ
\newcommand{\lhs}{% 左辺
    \mathrm{(LHS)}    %
}
\newcommand{\rhs}{% 右辺
    \mathrm{(RHS)}    %
}
\newcommand{\finite}{%
    \mathrm{finite}    % 
}
\newcommand{\hc}{%
    \mathrm{h.c.}    % 
}
\newcommand{\lagr}{% Lagrangian
    \marhcal{L}    % 
}
\newcommand{\lagrd}{% Lagrangian density
    \mathscr{L}    % need "mathsfs" package
}
\newcommand{\hamil}{% Hamiltonian
    \mathcal{H}    % 
}
\newcommand{\hamild}{% Hamiltonian density
    \mathscr{H}    % need "mathsfs" package
}

%% オーダー
\newcommand{\order}[1]{%
    \mathcal{O} \! \left( #1 \right)    % 
}

もちろん，これ以外にも定義しておいた方が良いコマンドがあるだろう．
適宜定義しておきたい．

参考

• 表記の哲学 - TeX Wiki

---

1. xparse.sty | CTAN から．「xparse パッケージでスゴイLaTeX マクロを作ろう！ - Qiita」に詳しい． ↩