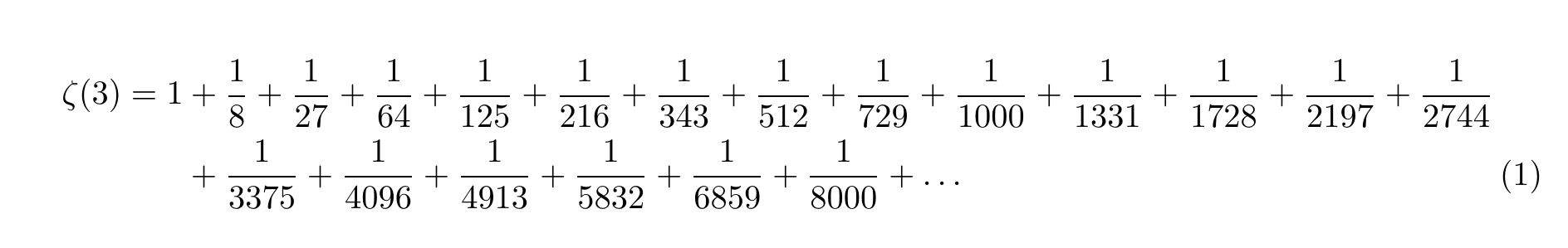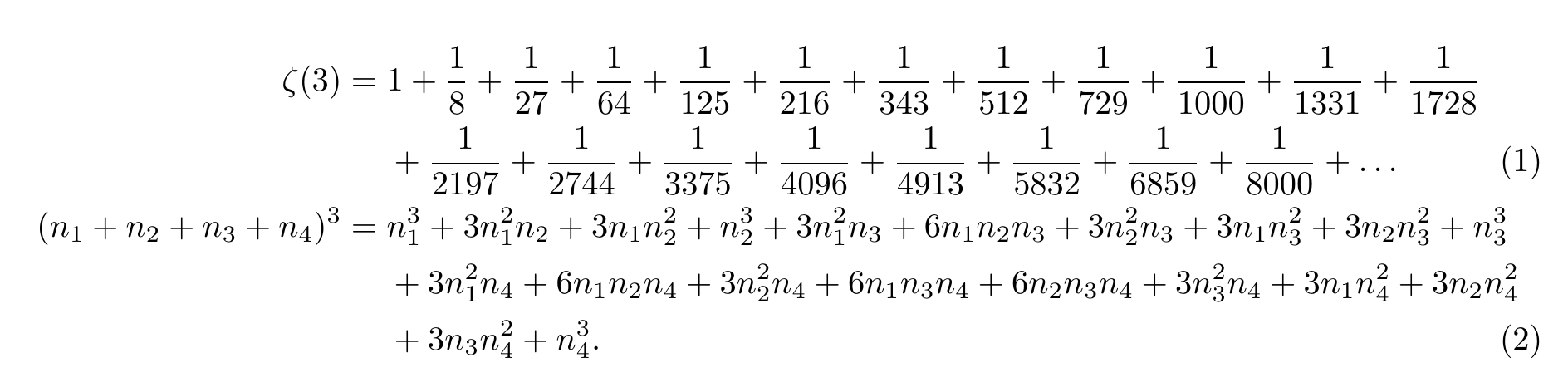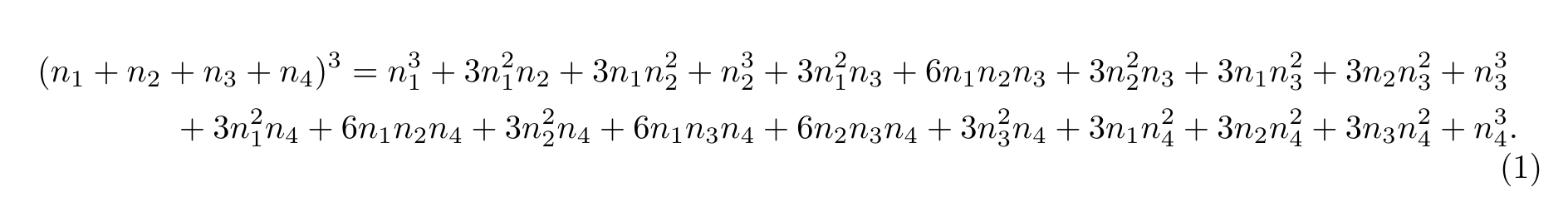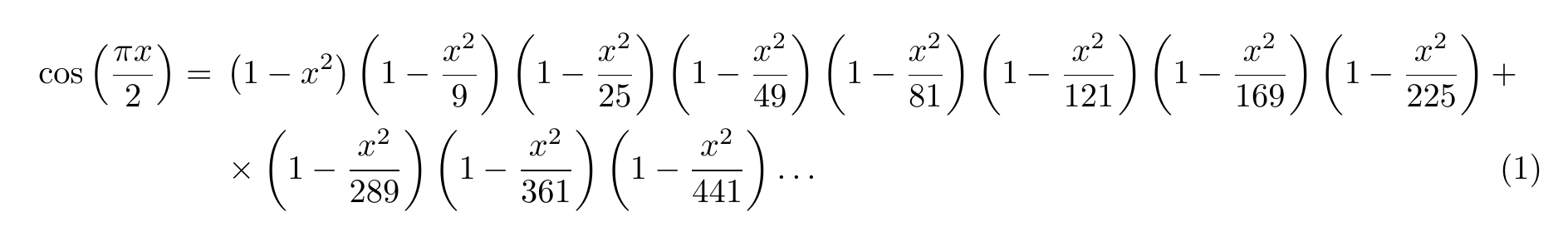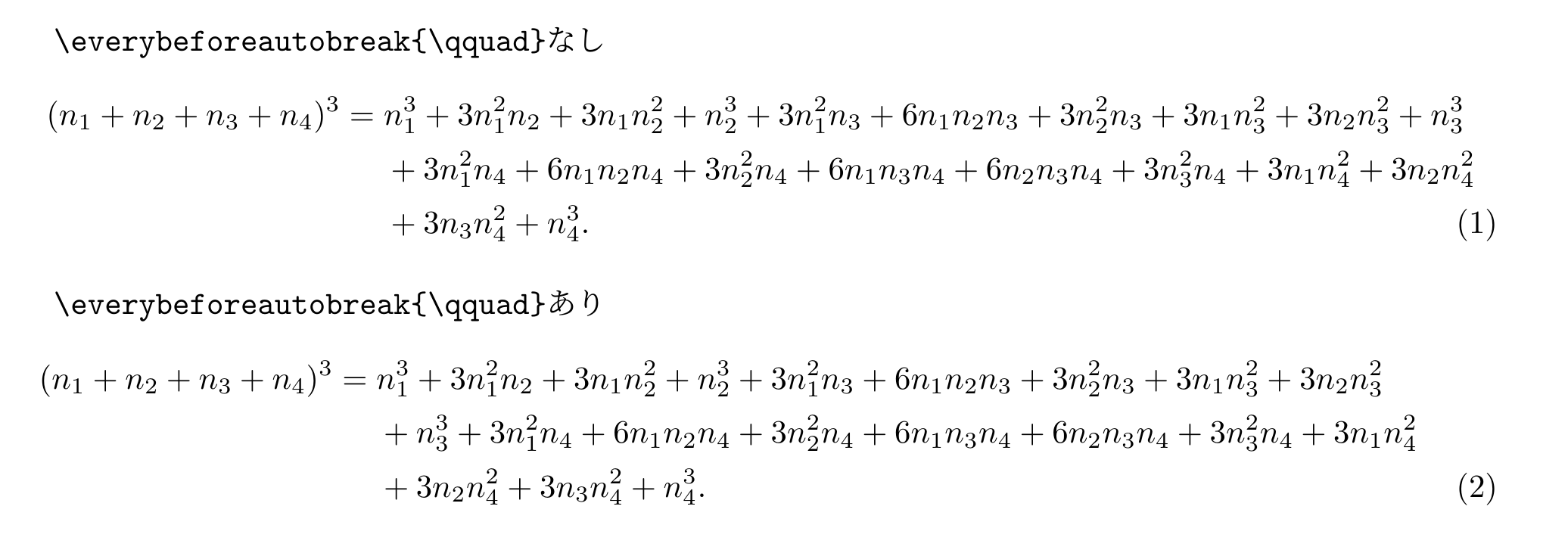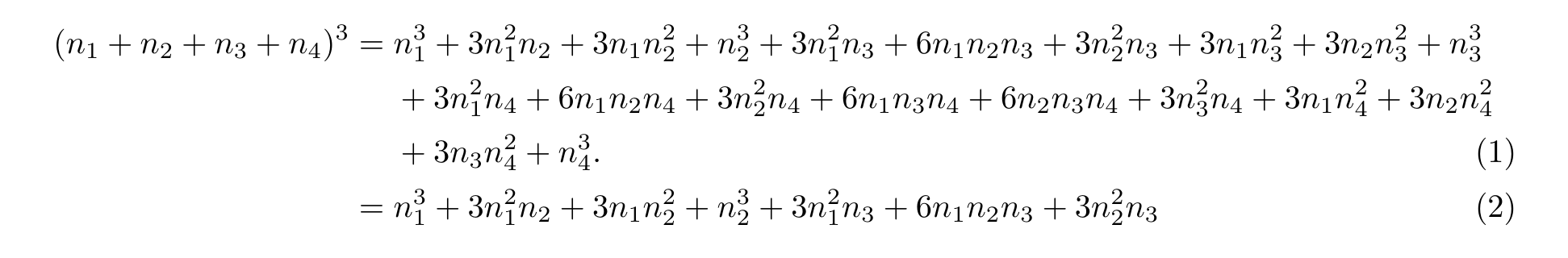Go to Qiita Advent Calendar 2024 Top
LoginSignup
2
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@Yarakashi_Kikohshi

autobreak を使いこなす

Last updated at Posted at 2020-08-20

※ コードが長ったらしくなっていますが，記事自体は非常に短いです．お気軽にご覧下さい．

autobreak ってなんぞ

amsmath パッケージに依存して，長い数式を自動改行してくれる素晴らしいパッケージ．雰囲気としては，split 環境が自動的に改行してくれる環境．

TeXLive2020 にも含まれている．含まれていない場合には以下から．

○ 使い方概要

  • autobreak 環境をalign 環境内で使用する（autobreak 環境の複数回の使用可）
  • autobreak 環境内の改行を出力される数式の改行可能ポイントとして認識される
  • 数式を外部ファイルとすることも可能
  • autobreak 環境で& や\\ を挿入することは出来ない
  • 式番号を付与しない場合には，(split 環境と同様に) align* 環境とする or \notag を使用する
  • align 環境内かつautobreak 環境外ではあまり綺麗な数式が出ない
  • amsmath パッケージのオプションではtbtags と同等の位置に式番号が付与される (参照節)

注意：autobreak 環境内にある改行を論理的に挿入できる改行可能ポイントとして解釈するので，改行をまたぐような\left~\right の対応を採ることは出来ない．
もし，改行の前後で括弧で閉じる必要がある場合には，\Bigl などを使用する必要がある．以下の記事で詳しく紹介しているので，参照してほしい．

■ パッケージ読み込み

autobreak パッケージはamsmath パッケージを自動的に読み込むが，明示的に読み込んでおいたほうが良い．

\usepackage[tbtags]{amsmath}
\usepackage{mathtools} % mathtools も入れておいた方がオススメ
\usepackage{autobreak}

amsmath のオプションでtbtags を指定している．これは，autobreak 環境で自動改行した数式がこのオプションと同等になっているからだ．(autobreak 環境はこのtbtags やcentertags の影響を受けないようだ)
また，leqno を指定すると，split 環境と異なる結果を得る．

amsmath のオプションに関しては以下の記事の「split 環境に関して」を参照してほしい．

以下の数式はパッケージガイドの式をそのまま援用している．

○ 実際に使ってみる

左辺，= ，右辺の表現方法が明確でないときちんと認識されないので注意が必要．

  • 左辺 : 一行にする（左辺の改行は出来ない）
  • = : 左辺の右側（ここでないと= が認識されないようだ）1
  • 右辺 : 改行で数式の改行可能ポイントを認識するので，和や積の部分で改行するようにする

以下のように数式を組もう．2

\begin{align}
    \begin{autobreak}
        \zeta(3) = % 左辺は1行で収める，"=" はココ
        1
        + \frac{1}{8}
        + \frac{1}{27}
        + \frac{1}{64}
        + \frac{1}{125}
        + \frac{1}{216}
        + \frac{1}{343}
        + \frac{1}{512}
        + \frac{1}{729}
        + \frac{1}{1000}
        + \frac{1}{1331}
        + \frac{1}{1728}
        + \frac{1}{2197} % この辺りで改行される
        + \frac{1}{2744}
        + \frac{1}{3375}
        + \frac{1}{4096}
        + \frac{1}{4913}
        + \frac{1}{5832}
        + \frac{1}{6859}
        + \frac{1}{8000}
        + \dots
    \end{autobreak}
\end{align}

autobreak-1eq.png

複数のautobreak 環境を実行すると以下のようになる．

\begin{align}
    \begin{autobreak}
        \zeta(3) =
        1
        + \frac{1}{8}
        + \frac{1}{27}
        + \frac{1}{64}
        + \frac{1}{125}
        + \frac{1}{216}
        + \frac{1}{343}
        + \frac{1}{512}
        + \frac{1}{729}
        + \frac{1}{1000}
        + \frac{1}{1331}
        + \frac{1}{1728}
        + \frac{1}{2197}
        + \frac{1}{2744}
        + \frac{1}{3375}
        + \frac{1}{4096}
        + \frac{1}{4913}
        + \frac{1}{5832}
        + \frac{1}{6859}
        + \frac{1}{8000}
        + \dots
    \end{autobreak}
\\
    \begin{autobreak}
    (n_1+n_2+n_3+n_4)^3 =
        n_1^3
        + 3 n_1^2 n_2
        + 3 n_1 n_2^2
        + n_2^3
        + 3 n_1^2 n_3
        + 6 n_1 n_2 n_3
        + 3 n_2^2 n_3
        + 3 n_1 n_3^2
        + 3 n_2 n_3^2
        + n_3^3
        + 3 n_1^2 n_4
        + 6 n_1 n_2 n_4
        + 3 n_2^2 n_4
        + 6 n_1 n_3 n_4
        + 6 n_2 n_3 n_4
        + 3 n_3^2 n_4
        + 3 n_1 n_4^2
        + 3 n_2 n_4^2
        + 3 n_3 n_4^2
        + n_4^3 .
    \end{autobreak}
\end{align}

autobreak-2eq.png

上下2つの式の= が揃う．
ただし，autobreak 環境の外に出るとまったく揃わない．また，& を付けてもダメ．
autobreak 環境を出て数式を揃えることも出来る．以下の「式を続けたい場合」を参照してください．

○ オプション

■ 改行後のインデント幅を変更する

mathtools と同様の\MoveEqLeft を用いることが出来る．3
デフォルトでは左マージンから2em になっており，これは任意に変更することが出来る．

\begin{align}
    \begin{autobreak}
    \MoveEqLeft[4]  % ここでは4em ずらすようにしている．ココでないとダメ．
    (n_1+n_2+n_3+n_4)^3 =
        n_1^3
        + 3 n_1^2 n_2
        + 3 n_1 n_2^2
        + n_2^3
        + 3 n_1^2 n_3
        + 6 n_1 n_2 n_3
        + 3 n_2^2 n_3
        + 3 n_1 n_3^2
        + 3 n_2 n_3^2
        + n_3^3
        + 3 n_1^2 n_4
        + 6 n_1 n_2 n_4
        + 3 n_2^2 n_4
        + 6 n_1 n_3 n_4
        + 6 n_2 n_3 n_4
        + 3 n_3^2 n_4
        + 3 n_1 n_4^2
        + 3 n_2 n_4^2
        + 3 n_3 n_4^2
        + n_4^3 .
    \end{autobreak}
\end{align}

autobreak-moveeqleft.png

\MoveEqLeft を知りたい場合には，「amsmath+mathtools と仲良くなろう #-数式にインデントを一括で入れたい - Qiita」を参照しても良いだろう．

■ 改行の前後でトークンを挿入する

  • 改行前にトークンを挿入する : \everybeforeautobreak{<token>}
  • 改行後にトークンを挿入する : \everyafterautobreak{<token>}

数式としてはおかしなものになっているが，これでどのように機能しているのか理解できるだろう．

\begin{align}
    \everybeforeautobreak{+} % 改行前に "+"
    \everyafterautobreak{\times} % 改行後に "×"
    \begin{autobreak}
    \cos\left(\frac{\pi x}{2}\right) =
        \left(1-x^2\right)
        \left(1-\frac{x^2}{9}\right)
        \left(1-\frac{x^2}{25}\right)
        \left(1-\frac{x^2}{49}\right)
        \left(1-\frac{x^2}{81}\right)
        \left(1-\frac{x^2}{121}\right)
        \left(1-\frac{x^2}{169}\right)
        \left(1-\frac{x^2}{225}\right)
        \left(1-\frac{x^2}{289}\right)
        \left(1-\frac{x^2}{361}\right)
        \left(1-\frac{x^2}{441}\right)
        \dots
    \end{autobreak}
\end{align}

autoreak-plustimes.png

改行前にトークンを挿入する場合があるのかいささか疑問に感じていたが，以下のような使い方は良いかもしれない．

autobreak-qquad.png

各塊の大きさによっては式番号に近すぎることが生じる．これを解消するために，空白を挿入すると解消させることが出来る．(これはBad method かも知れないので，自己判断で利用してください．)

○ 式を続けたい場合

長い数式の式変形を長々と表記しても見ずらいだけなように思うが， 以下のようにすれば良い．

\begin{align}
    \begin{autobreak}
    (n_1+n_2+n_3+n_4)^3 =
        n_1^3
        + 3 n_1^2 n_2
        + 3 n_1 n_2^2
        + n_2^3
        + 3 n_1^2 n_3
        + 6 n_1 n_2 n_3
        + 3 n_2^2 n_3
        + 3 n_1 n_3^2
        + 3 n_2 n_3^2
        + n_3^3
        + 3 n_1^2 n_4
        + 6 n_1 n_2 n_4
        + 3 n_2^2 n_4
        + 6 n_1 n_3 n_4
        + 6 n_2 n_3 n_4
        + 3 n_3^2 n_4
        + 3 n_1 n_4^2
        + 3 n_2 n_4^2
        + 3 n_3 n_4^2
        + n_4^3 .
    \end{autobreak}
\\
    = {} &
        n_1^3
        + 3 n_1^2 n_2
        + 3 n_1 n_2^2
        + n_2^3
        + 3 n_1^2 n_3
        + 6 n_1 n_2 n_3	
        + 3 n_2^2 n_3
\end{align}

autobreak-good.png

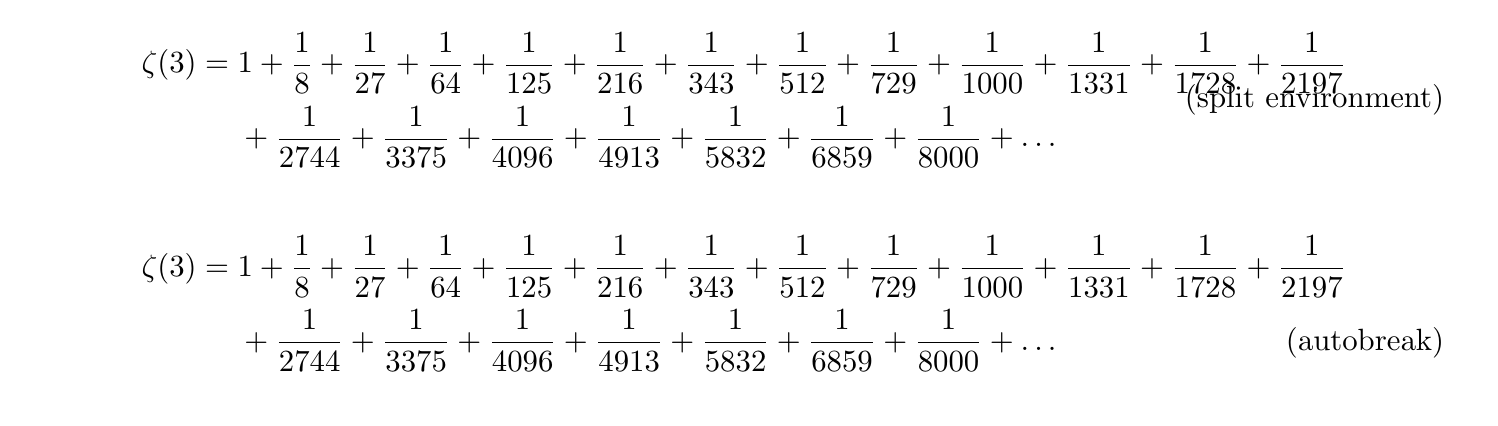
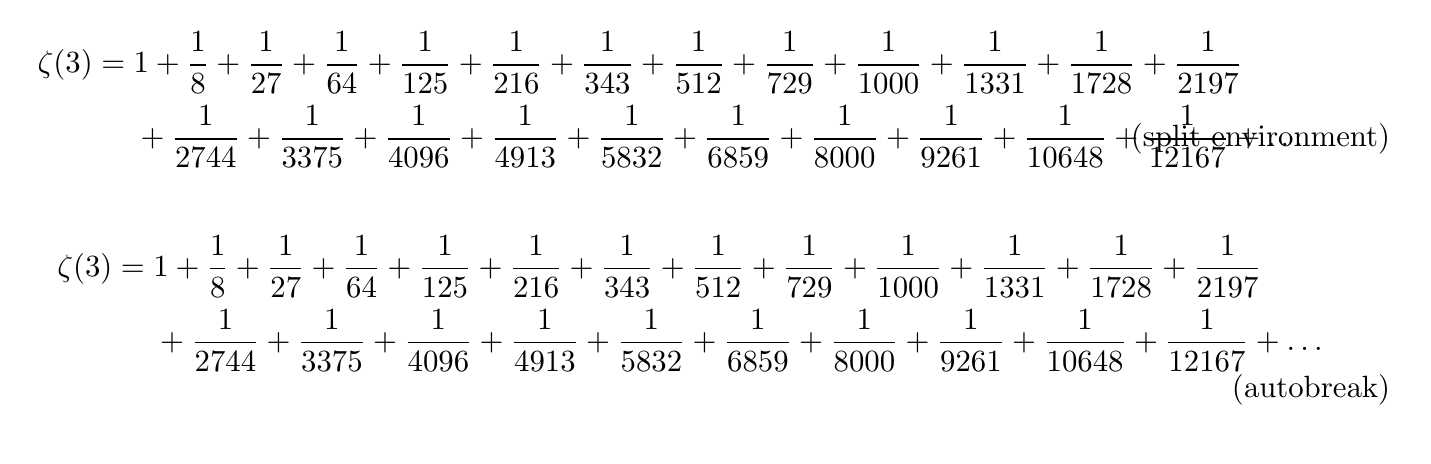
○ split 環境と比較してみた

autobreak 環境の改行位置に合わせる形でsplit 環境で同じ数式を出力させ，amsmath のオプションを変更することで，autobreak とsplit を比較してみる．

autobreak とsplit の比較コード (折りたたみ) 
\begin{equation}
    \begin{split}
        \zeta(3) = {} & 1 + \frac{1}{8} + \frac{1}{27} + \frac{1}{64} + \frac{1}{125}
        + \frac{1}{216} + \frac{1}{343} + \frac{1}{512} + \frac{1}{729}
        + \frac{1}{1000} + \frac{1}{1331} + \frac{1}{1728} + \frac{1}{2197} \\
      & + \frac{1}{2744} + \frac{1}{3375} + \frac{1}{4096} + \frac{1}{4913}
        + \frac{1}{5832} + \frac{1}{6859} + \frac{1}{8000} + \dots
    \end{split}  \tag{split environment}
\end{equation}

\begin{align}
    \begin{autobreak}
        \zeta(3) =
        1
        + \frac{1}{8}
        + \frac{1}{27}
        + \frac{1}{64}
        + \frac{1}{125}
        + \frac{1}{216}
        + \frac{1}{343}
        + \frac{1}{512}
        + \frac{1}{729}
        + \frac{1}{1000}
        + \frac{1}{1331}
        + \frac{1}{1728}
        + \frac{1}{2197}
        + \frac{1}{2744}
        + \frac{1}{3375}
        + \frac{1}{4096}
        + \frac{1}{4913}
        + \frac{1}{5832}
        + \frac{1}{6859}
        + \frac{1}{8000}
        + \dots
    \end{autobreak}  \tag{autobreak}
\end{align}

\tag で式番号を変更した．これはsplit もautobreak も同様の位置に置くことで変更することが出来た．

● centertags を指定

まずはcentertags を指定した．オプションの明記 / 不明記に問わず同様の結果となった．

autobreak-centertags.png

若干，式番号の出力させる位置が異なるか．

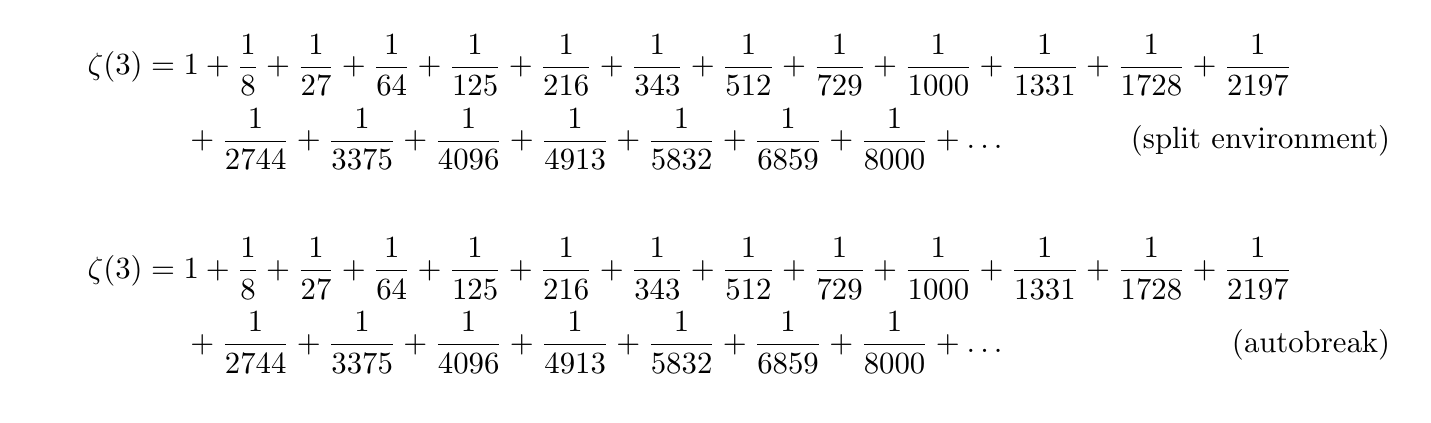
● tbtags を指定

tbtags に変更してみると以下のようになった．

autobreak-split-short.png

これを見ると，autobreak は自動的にtbtags と同等の結果を得るということが分かる．この結果を思えば，autobreak 環境を使用する際にはsplit 環境と平行して使用することを想定してtbtags をオプションとして追加しておくべきだろうと思われる．

また，項数を少し増やしてみた．すると，以下のような結果を得た．

autobreak-split-long.png

どういうわけだが，split 環境では式番号と数式がオーバーラップしてしまうがautobreak 環境では避けるようになった．4

● leqno を指定

また，leqno を指定してみた．やはりこれも同等の結果を得られるというわけではなかった．

autobreak-leqno-tbtags.png

式番号の位置が異なっていることが分かる．

● 比較まとめ

以上の結果をまとめると以下のようになる．

  • split 環境と同等の結果を得るには，amsmath のオプションをtbtags 指定する必要がある
  • split 環境では式番号に被ってしまうような数式であっても，自動的に避けてくれる
  • leqno を指定すると同等の結果を得ない5 (tbtags と同時に指定するとより顕著になる)

余談

autobreak 環境を利用すれば，split 環境よりも簡単に数式の改行を行うことが出来る．その反面，紙面サイズや余白を変更することでレイアウトが崩れる．
自動化をしたことによる不便な部分である．レイアウトが崩れることに対してはそれほど気にしない場合であればまったく問題ない．

もし，レイアウトが崩れることを気にする立場にあるならば，autobreak 環境で当たりを付けて，split 環境に置き換えるということをしても良いのかもしれない．これの他に幸せな環境があれば，そちらを使った方が良いかも知れない．

上のソースコードの改行を減らしてみると自動改行される位置が変化して面白いので，ぜひ試してみてほしい．

ちなみに，ユーザガイドはPDF で19ページであり，11ページは実装されているコードと索引なので，8ページしか$\rm\LaTeX$ ユーザが読むべき部分はない．この部分は簡単に読みきれるのでぜひ．($\rm\TeX$ に詳しい方は読むと良いかも知れません．)
実は別ファイルの数式を挿入する方法は紹介していない...

追記

  • 2020/08/12 : autobreak 環境を使用した状態で式を続けることが出来ないと紹介していましたが，\MoveEqLeft を使用しているものと同様の手続きで対応することが出来ることに気付いたので修正しました．
  • 2020/08/18 : 改行後のトークンに空白を入れることで式番号と数式の間隔を空ける方法を紹介しました．
  • 2020/09/03 : 「split 環境と比較してみた」を追加しました．

  1. 等号= 以外にも，\simeq や\coloneqq 等でも良い．この辺りの違いはよく分かっていない．（出来ない記号があるのかも不明．等号関連は他の記号とは異なる取り扱いをしている?） ↩

  2. 改行される付近で% を付けると少し挙動が変化する．これは何? ↩

  3. autobreak パッケージで\MoveEqLeft が独自に定義されているようだ．おそらくはmathtools から提供されている同様の\MoveEqLeft と競合することはないと思われる． ↩

  4. split 環境を使用して式番号と数式がオーバーラップする場合の回避方法を知らない．知っている方があれば教えてほしい． ↩

  5. これらの結果から考えるに，tbtags と同等の位置に式番号が出るようになっているだけで，同様のシステムで処理されているわけではないようだ． ↩

2
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?