はじめに
量子力学において,量子状態を記述するための標準的な記法としてブラケット記法が
挙げられる.
量子コンピュータを学ぶにあたり,身に着けたほうがよいものだと感じたので,
基本的なことなどをまとめる.
ブラケット記法とは
ブラケット記法(ディラックの記法)とは,
量子力学における量子状態を記述するための標準的な記法である.
ブラケット記法では,量子状態をブラ($\langle φ|$)とケット($|ψ\rangle$と呼ばれる2つのベクトルで表す.
ブラは横ベクトル,ケットは縦ベクトルである.
ブラとケットの内積は$\langle φ|ψ\rangle$のように$\langle \rangle$を括弧のように見立てたときに成立する.
覚えておきたい数式
横ベクトル(ブラ)
\langle 0| = (1\quad 0)
\langle 1| = (0\quad 1)
\langle 00| = (1\quad 0\quad 0\quad 0)
\langle 01| = (0\quad 1\quad 0\quad 0)
\langle 10| = (0\quad 0\quad 1\quad 0)
\langle 11| = (0\quad 0\quad 0\quad 1)
縦ベクトル(ケット)
|0\rangle
=
\left(
\begin{matrix}
1 \\
0
\end{matrix}
\right)
|1\rangle
=
\left(
\begin{matrix}
0 \\
1
\end{matrix}
\right)
|00\rangle
=
\left(
\begin{matrix}
1 \\
0 \\
0 \\
0
\end{matrix}
\right)
|01\rangle
=
\left(
\begin{matrix}
0 \\
1 \\
0 \\
0
\end{matrix}
\right)
|10\rangle
=
\left(
\begin{matrix}
0 \\
0 \\
1 \\
0
\end{matrix}
\right)
|11\rangle
=
\left(
\begin{matrix}
0 \\
0 \\
0 \\
1
\end{matrix}
\right)
内積
\langle 0|0\rangle = 1
\langle 0|1\rangle = 0
\langle 1|0\rangle = 0
\langle 1|1\rangle = 1
行列
|0\rangle \langle 0|
=
\left(
\begin{matrix}
1 & 0\\
0 & 0
\end{matrix}
\right)
|0\rangle \langle 1|
=
\left(
\begin{matrix}
0 & 1\\
0 & 0
\end{matrix}
\right)
|1\rangle \langle 0|
=
\left(
\begin{matrix}
0 & 0\\
1 & 0
\end{matrix}
\right)
|1\rangle \langle 1|
=
\left(
\begin{matrix}
0 & 0\\
0 & 1
\end{matrix}
\right)
その他
恒等演算子
I
=
|0\rangle \langle0| + |1\rangle \langle1|
=
\left(
\begin{matrix}
1 & 0\\
0 & 1
\end{matrix}
\right)
Xゲート
X
=
|0\rangle \langle 1| + |1\rangle \langle 0|
=
\left(
\begin{matrix}
0 & 1\\
1 & 0
\end{matrix}
\right)
Hゲート
H
=
\frac{1}{\sqrt{2}}(|0\rangle \langle 0| + |0\rangle \langle 1| + |1\rangle \langle 0| - |1\rangle \langle 1|)
=
\frac{1}{\sqrt{2}}
\left(
\begin{matrix}
1 & 1\\
1 & -1
\end{matrix}
\right)
CNOTゲート
CNOT = |0\rangle \langle 0| ⊗I + |1\rangle \langle 1|⊗X
=
\left(
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0
\end{matrix}
\right)
計算例1
入力$|10\rangle$へCNOTゲートを作用.
\begin{align}
CNOT|10\rangle
&= (|0\rangle \langle 0| ⊗I + |1\rangle \langle 1|⊗X)|10\rangle\\
&= (|0\rangle \langle 0| ⊗I)|10\rangle + (|1\rangle \langle 1|⊗X)|10\rangle\\
&= |0\rangle \langle0||1\rangle⊗I|0\rangle + |1\rangle \langle1||1\rangle⊗X|0\rangle\\
&= 0 + |1\rangle ⊗ |1\rangle (理由:\langle 0|1\rangle = 0,\langle 1|1\rangle = 1,Xはビット反転のため) \\
&= |11\rangle
\end{align}
計算例2
以下の回路で入力$|00\rangle$のときの$|x\rangle$
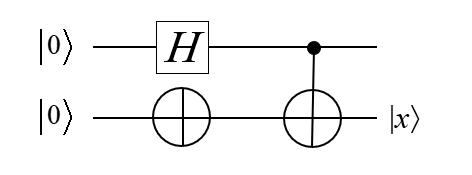
HゲートとXゲートの作用まで
\begin{align}
H|0\rangle ⊗ X|0\rangle((H⊗X)|00\rangleと同じ)
&= \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) ⊗ |1\rangle\\
&=\frac{1}{\sqrt{2}}|01\rangle + \frac{1}{\sqrt{2}}|11\rangle
\end{align}
これにCNOTを作用させたものが$|x\rangle$
\begin{align}
|x\rangle
&= CNOT(\frac{1}{\sqrt{2}}|01\rangle + \frac{1}{\sqrt{2}}|11\rangle)\\
&= \frac{1}{\sqrt{2}}|01\rangle + \frac{1}{\sqrt{2}}|10\rangle
\end{align}
最後に
ブラケット記法で量子計算をする際には,特に内積と行列の関係は押さえておきたい.
次回は量子コンピュータから離れて,SATについて扱う.