はじめに
前回の記事の続きで,複数量子ビットを扱う基本的な量子ゲートに注目する.
制御ビットとコントロールビット
制御ビット(コントロールビット) は,そのままの状態で出力される量子ビット.
標的ビット(ターゲットビット) は,制御ビットの内容によって,出力が変化する量子ビット.
CNOTゲート
制御ビットが$|1\rangle$のとき,標的ビットにXゲートを適用(ビット反転) するゲート.
$CNOT$ゲートの行列表現は以下のようになる.
CNOT =
\left(
\begin{matrix}
I & O\\
O & X
\end{matrix}
\right)
=
\left(
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0
\end{matrix}
\right)
量子回路の例は以下のようになる.
このとき,上にある量子ビットが制御ビット,下にある量子ビットが標的ビットとなる.

ブラケット記法では,以下のようになる.
$CNOT = |0\rangle \langle 0| ⊗ I + |1\rangle \langle 1| ⊗ X$
エンタングルメント状態
エンタングルメント状態とは,量子状態の操作でとある量子を観測した際に,
ほかの量子の状態に影響を与えてしまう状態のこと.
簡単に言うと一方さえ分かれば,もう一方を確定することができる状態のことである.
例えば,以下のような量子回路があるとする.
このとき,制御ビットは1/2の確率で0か1が観測される量子ビットである.
したがって,制御ビットを観測した際には0か1が観測される.
$CNOT$ゲートを適用したとき,標的ビットでは何が観測されるかを考える.
その結果は,制御ビットで何が観測されるかによって,標的ビットの観測される結果が決まる.
制御ビットを観測した結果が0であれば標的ビットは0が観測され,
制御ビットを観測した結果が1であれば標的ビットは1が観測される.
これがエンタングルメント状態だが,
CNOTゲートを用いるとこの状態を生成することが可能である.
エンタングルメント状態の生成
例1
制御ビットを,$\frac{1}{\sqrt2}(|0\rangle + |1\rangle )$,標的ビットを$|0\rangle$とするときを考える.
このとき,初期状態は以下となる.
\frac{1}{\sqrt2}(|0\rangle + |1\rangle )|0\rangle = \frac{1}{\sqrt2}(|0\rangle |0\rangle+ |1\rangle |0\rangle)
これは,以下を示す.
- 1つ目の量子ビットが$|0\rangle$,2つ目の量子ビットが$|0\rangle$となる確率は1/2
- 1つ目の量子ビットが$|1\rangle$,2つ目の量子ビットが$|0\rangle$となる確率は1/2
このとき,1つ目の量子ビットを制御ビット,2つ目の量子ビットを標的ビットとする.
この場合はエンタングルメント状態ではない.
理由は以下の点が挙げられる.
- 標的ビットを観測したとき,制御ビットが一意に観測できない.
- $\frac{1}{\sqrt2}(|0\rangle |0\rangle+ |1\rangle |0\rangle) = \frac{1}{\sqrt2}(|0\rangle + |1\rangle )|0\rangle =$となり,制御ビットの状態と標的ビットの状態を分離状態として書けない.
※分離状態とは,全体の状態を"$制御ビット⊗標的ビット$"として書けること
続いて,これに$CNOT$ゲートを作用させると,どうなるかを考えると以下のようになる.
\frac{1}{\sqrt2}(|0\rangle |0\rangle+ |1\rangle |1\rangle)
このようになるのは$CNOT$ゲートは,制御ビットが$|1\rangle$となるとき,
標的ビットを反転させるためである.
これは以下を示す.
- 1つ目の量子ビットが$|0\rangle$,2つ目の量子ビットが$|0\rangle$となる確率は1/2
- 1つ目の量子ビットが$|1\rangle$,2つ目の量子ビットが$|1\rangle$となる確率は1/2
この結果からわかる通り,制御ビットまたは標的ビットを観測した際に,
もう一方の状態が一意に定まり,エンタングルメント状態を生成できていることがわかる.
例2
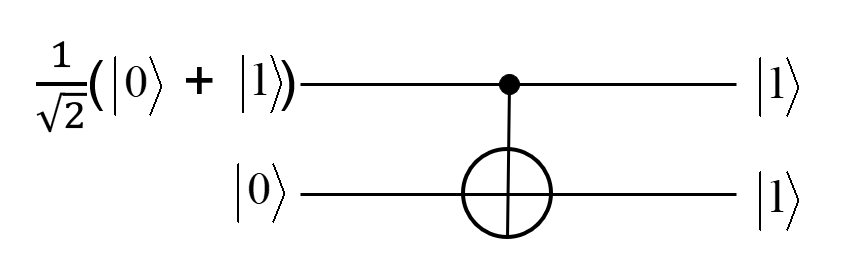
制御ビットを,$\frac{1}{\sqrt2}(|0\rangle + |1\rangle )$,標的ビットを$|1\rangle$とするときを考える.
このとき,初期状態は以下となる.
\frac{1}{\sqrt2}(|0\rangle + |1\rangle )|1\rangle = \frac{1}{\sqrt2}(|0\rangle |1\rangle+ |1\rangle |1\rangle)
続いて,これに$CNOT$ゲートを作用させると,どうなるかを考えると以下のようになる.
\frac{1}{\sqrt2}(|0\rangle |1\rangle+ |1\rangle |0\rangle)
この場合もエンタングルメント状態になっていることが確認できる.
SWAPゲート
2量子ビットを交換するゲート.
$SWAP$ゲートの行列表現は以下のようになる.
SWAP
=
\left(
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0
\end{matrix}
\right)
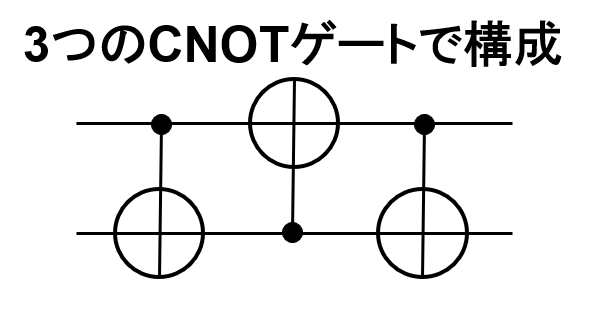
量子回路の例は以下のようになる.
また,その内訳は3つのCNOTゲートとなっている.
CNOTゲート3つで交換できる理由(数式的に)
続いて,$CNOTゲート$を3つ用いることで量子ビットを交換できる理由を確認する.
初期状態
ここで,2つの2量子ビットのうち制御ビットを$q_1$,ターゲットビットを$q_2$とする.
この場合,初期状態は以下のように表せる.
(2量子ビットの入力は$|00\rangle, |01\rangle, |10\rangle, |11\rangle$のいずれかのため)
q_1⊗q_2 = a|00\rangle + b|01\rangle + c|10\rangle + d|11\rangle
CNOTを適用(1回目)
これに一回$CNOT$ゲートを適用することを考えると,以下のようになる.
(1つ目の量子ビットが1のとき,2つ目の量子ビットを反転)
CNOT(a|00\rangle + b|01\rangle + c|10\rangle| + d|11\rangle) = a|00\rangle + b|01\rangle + d|10\rangle + c|11\rangle
この結果から,$|10\rangle, |11\rangle$の係数が入れ替わっていることがわかる.
CNOTを適用(2回目)
この出力されたものを制御ビットとしてCNOTを適用することを考えると,以下のようになる.
(2つ目の量子ビットが1のとき1つ目の量子ビットを反転)
CNOT(a|00\rangle + b|01\rangle + d|10\rangle| + c|11\rangle) = a|00\rangle + c|01\rangle + d|10\rangle + b|11\rangle
この結果から,$|01\rangle, |11\rangle$の係数が入れ替わっていることがわかる.
CNOTを適用(3回目)
さらに,出力されたものを制御ビットとして$CNOT$を適用することを考える.
(1つ目の量子ビットが1のとき,2つ目の量子ビットを反転)
CNOT(a|00\rangle + c|01\rangle + d|10\rangle + b|11\rangle) = a|00\rangle + c|01\rangle + b|10\rangle + d|11\rangle
この結果から,$|10\rangle, |11\rangle$の係数が入れ替わっていることがわかる.
結論
以上より,初期状態と最後の状態$a|00\rangle + c|01\rangle + b|10\rangle + d|11\rangle$に注目すると,
$|01\rangle, |10\rangle$の係数が入れ替わっていることが確認できる.
これは,00,11を入力されているときはその出力は変化しないが,01が入力されたときは10,10が入力されたときは01が出力されることを意味している.
直感的には,
2つの量子ビットを並べる順番(制御ビットとターゲットビットの位置)を逆にして
項を並べかえたのと同じである.
数式的に確認するならば,$q_1 = e|0\rangle + f|1\rangle, q_2 = g|0\rangle + h|1\rangle$としたとき,
それぞれのテンソル積を考えると以下のようになる.
q_1⊗q_2 = eg|00\rangle + eh|01\rangle + fg|10\rangle + fh|11\rangle = a|00\rangle + b|01\rangle + c|10\rangle + d|11\rangle
q_2⊗q_1 = ge|00\rangle + gf|01\rangle + he|10\rangle + hf|11\rangle = a|00\rangle + c|01\rangle + b|10\rangle + d|11\rangle
したがって,$q_1, q_2$を入れかえたときのテンソル積の値が最後の状態と一致している
($a|00\rangle + c|01\rangle + b|10\rangle + d|11\rangle$となる)ことが確認できる.
これらから,$CNOT$ゲートを3つ用いることで2量子ビットを交換できることがわかる.
最後に
エンタングルメント状態の理解は深まったが,量子回路でゲートを適用したときの演算や,
その結果を直感的に導き出すことが(自分にとって)難しい.
なので,数式や行列,ブラケット記法の解釈をできるように次回以降の記事で扱いたい.