はじめに
本記事は競技プログラミングにおいて解くのに困った問題について、なぜその解法に思い至るのか、どのような所でハマったか等のポイントをメモした、筆者の筆者による筆者のための備忘録となっております。読まれることを意識していないので文章がとっ散らかってます。
また、本記事を書くにあたりこちらの記事を多分に参考にさせて頂いております。ありがとうございます。
問題
問題はこちら。
問題文
長さ$N$の整数列$A$があります。
あなたは今からこの数列について$Q$個のクエリを処理します。$i$番目のクエリでは、 $T_i, X_i, Y_i$が与えられるので、以下の処理をしてください。
-
$T_i=1$のとき
$A_{X_i}$を$A_{X_i} \oplus Y_i$で置き換える。 -
$T_i=2$のとき
$A_{X_i}\oplus A_{X_{i+1}} \oplus A_{X_{i+2}}\oplus ... \oplus A_{Y_i}$ を出力する。
ただし$a\oplus b$は$a$と$b$のビット単位 xor を表します。
提出解答
提出解答はこちら。
size, q = map(int, input().split())
a = list(map(int, input().split()))
# 葉の数がlistのサイズ以上になるように完全2分木を作る。
n = 1
while n < size:
n *= 2
node = [0]*(2*n-1)
# n-1, ..., n+size-2にaを入れる。n+size-1, ..., 2n-2は0(xorでの単位元)で、影響を与えない。
for i in range(size):
node[i+n-1] = a[i]
# node[i] = node[2i+1]^node[2i+2]で、葉以外のノードであるnode[n-2], ..., node[0]を更新して行く
for i in range(n-2, -1, -1):
node[i] = node[2*i+1] ^ node[2*i+2]
def update(i, x): #a[i]をxで更新する
i += n-1
node[i] = x
while i > 0:
i = (i-1)//2 #2i+1, 2i+2(子ノード)からi(親ノード)に行くには、1引いて2で切り捨て割り算すればok
node[i] = node[2*i+1] ^ node[2*i+2]
def fold(L, R): #a[L]^a[L+1]^...^a[R-1]を出力する
L += n-1
R += n-1
vL = 0
vR = 0
while R > L:
if L % 2 == 0:
vL ^= node[L]
L += 1
if R % 2 == 0:
vR ^= node[R-1]
L = (L-1)//2
R = (R-1)//2
return (vL^vR)
ret = []
for i in range(q):
t, x, y = map(int, input().split())
x -= 1
if t == 1:
update(x, node[x+n-1]^y)
else:
ret.append(fold(x, y))
for v in ret:
print(v)
XORって?
私はこのページをみて勉強しました。要は二進数が関係した二項演算だと思っておけば大丈夫な気がします。Pythonにおいて$a$と$b$のxor演算は
print(a^b)
のように求めることができます。$\LaTeX$などでのべき乗の記号と同じなので注意したいですね。
さて、いくつかxor演算の性質について見ていきましょう。
- $(a\oplus b) \oplus c = a \oplus (b \oplus c)$ (結合法則)
- $a\oplus 0 = a$ (0は単位元)
- $a\oplus a = 0$ (逆元は自分自身)
だいたい上のことがわかっていれば問題ない気がしています。
部分和を求めるには?
ただ部分和を求めるだけならば、足し算と同様にして、累積和を計算することで計算することができます。数列$a_1, a_2,...,a_n$に対して、部分和$a_i \oplus...\oplus a_j$は、累積和を用いて、
$$(\oplus_{k=1}^{j}a_k) \oplus (\oplus_{l=1}^{i-1}a_l)$$
と表されます。$a_1,...,a_{i-1}$が2回計算されているため、前項の3つ目の性質により打ち消し合います。累積和は$O(n)$で求まり、各部分和は$O(1)$で求まります。
当初このやり方しか部分和の計算法を知らなかった私はこの方法で取り組みました。しかし今回は部分和を出力するだけではなく、値の更新が行われます。「累積和の更新が$O(1)$でできるような魔法無いかな~~~」と頭を捻っていましたが、そんな魔法は存在しなかったようです。その代わりにセグメント木という魔法が見つかりました。今回はこの出会いについて語っていきます。
セグメント木って?
まず、セグメント木というデータ構造において扱える量がどのような量なのかについて見ていきます。これはモノイドというものです。モノイドの定義を見ていきます。
モノイドの定義
集合$S$上に、二項演算($S$中の2つの要素を決めると、$S$中の1つの要素が定まる演算規則)$・$が定義されていて、
- 任意の$a,b,c$に対し$a・(b・c) = (a・b)・c$が成り立つ(結合法則)
- $S$の元$e$がただ一つ存在し、$a・e=e・a=a$が成り立つ(単位元の存在)
という性質を満たすとき、この集合、二項演算、単位元の組$(S,・,e)$をモノイドと言う(記法上、単位元が省略されることが多い)。
例えば、整数と足し算の組はモノイドです。今回扱うxor演算と自然数の集合との組はモノイドになります。なのでセグメント木で扱える対象になります。
さて、セグメント木という言葉が幾度か出てきましたが、これはどういった物なのでしょうか。まずできることを書いていきます。数列$a_1,...,a_n$に対して
- $a_i$の値を更新する。
- $a_i・...・a_j$の値を求める。
上の2つの操作をそれぞれ$O(\log n)$で行うことができます。セグメント木を構成するのに$O(n)$かかるので、めちゃくちゃ早く計算できます。幸せです。元の問題はモロ上の2つの操作を行う問題ですから、セグメント木を理解できればこの問題を解くことができますね。計算量は各クエリが$O(\log N)$でできるので、2分木の初期化も含めて$O(N+Q\log N)$くらいでしょうか。適当を言っているかもしれません。
さて、どのようなことをすれば上のような魔法を実現することができるんでしょうか?それではセグメント木がどのような構造をしているかを見て行きましょう。今、簡単のためにまずは$n=2^k$と表せるときに限定して考えましょう。
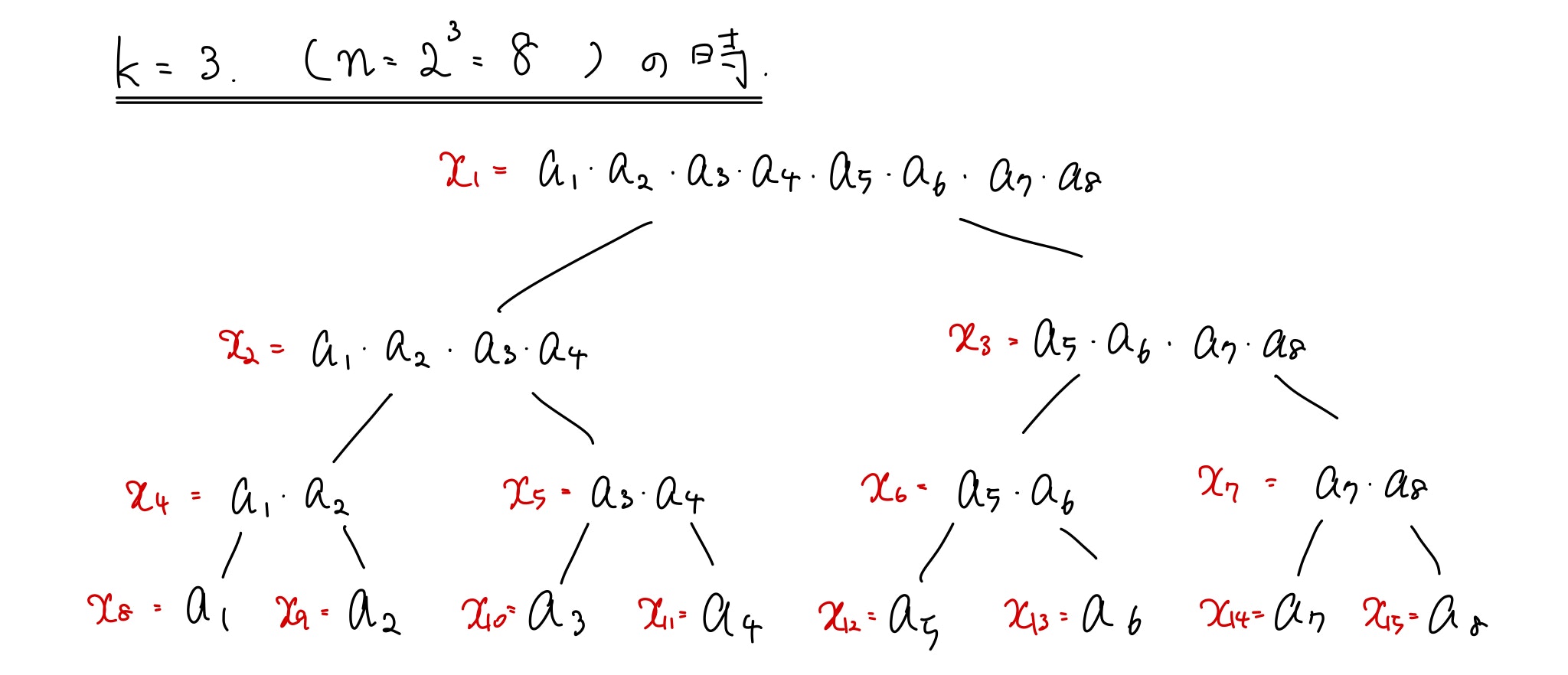
上の画像のように配列$x$を作ると、配列$x$は完全2分木を成します。$x_i$の子は$x_{2i}, x_{2i+1}$であり、
$$x_i = x_{2i}・x_{2i+1}$$
が成立しています。このような形をした木構造のことをセグメント木と言います。
ノードの個数を数えておきましょう。最下層は$n=2^k$個であり、そこから一つ上の層に行くごとに$2^{k-1}, 2^{k-2}, ..., 2, 1$個とノードが減っていくので、全部で
$$2^k + 2^{k-1} + 2^{k-2} + ... + 2 + 1 = 2^{k+1}-1 = 2n-1$$
個のノードがあります。
各種操作
ではまず更新操作を見てみましょう。例えば上の木で$a_6$を更新すると、どうしたらいいでしょうか。
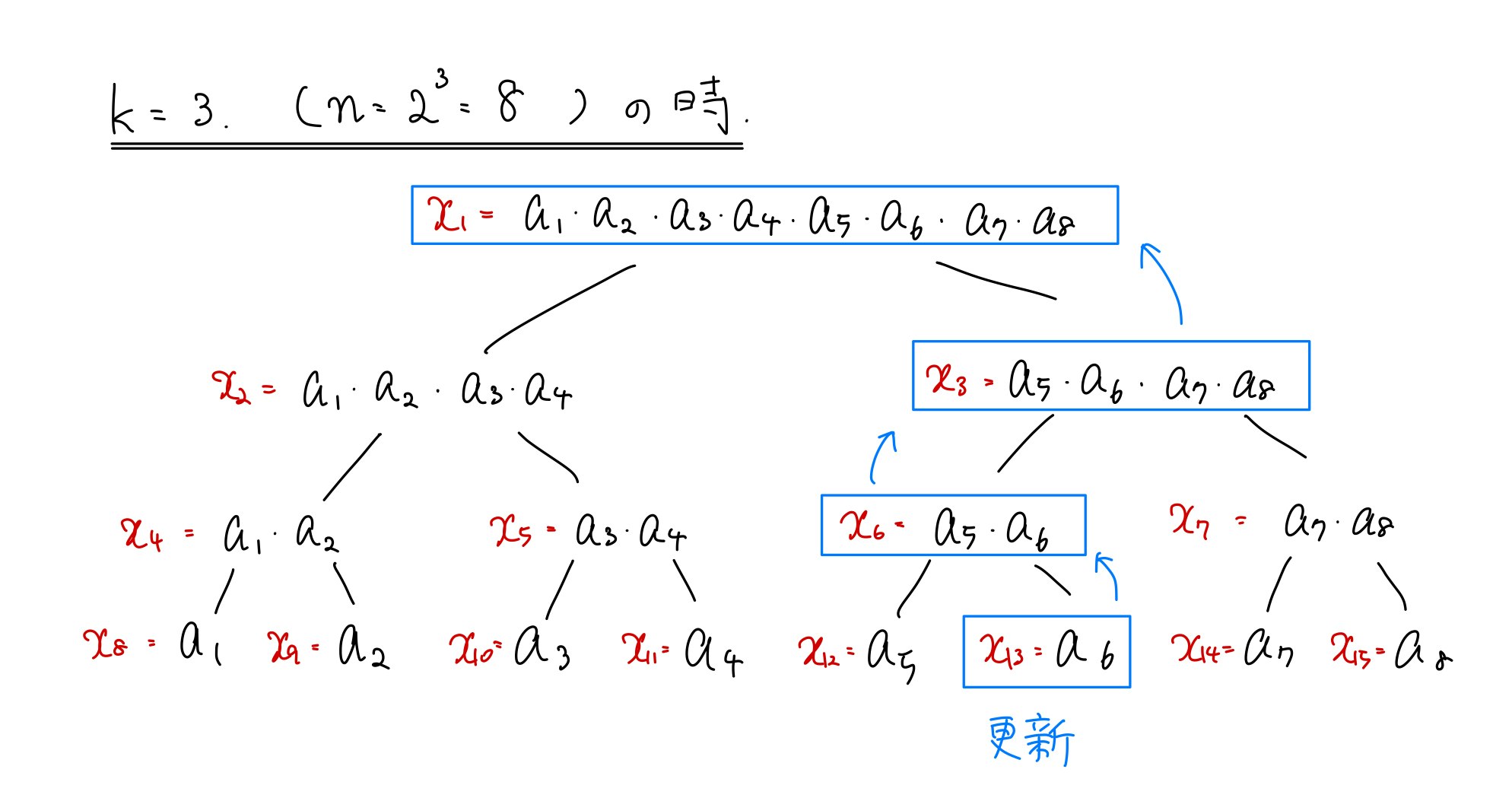
上の図のように、更新するノードから親ノードへと遡っていき、$x_1, x_3, x_6, x_{13}$を更新すれば良いです。更新するのは層の個数分のノードですから、計算量は$O(\log n)$となります。
では次に、指定の区間に対して$a_i・...・a_j$の値を求める操作を見てみましょう。例えば$a_2・a_3・...・a_7$を求めてみましょう。
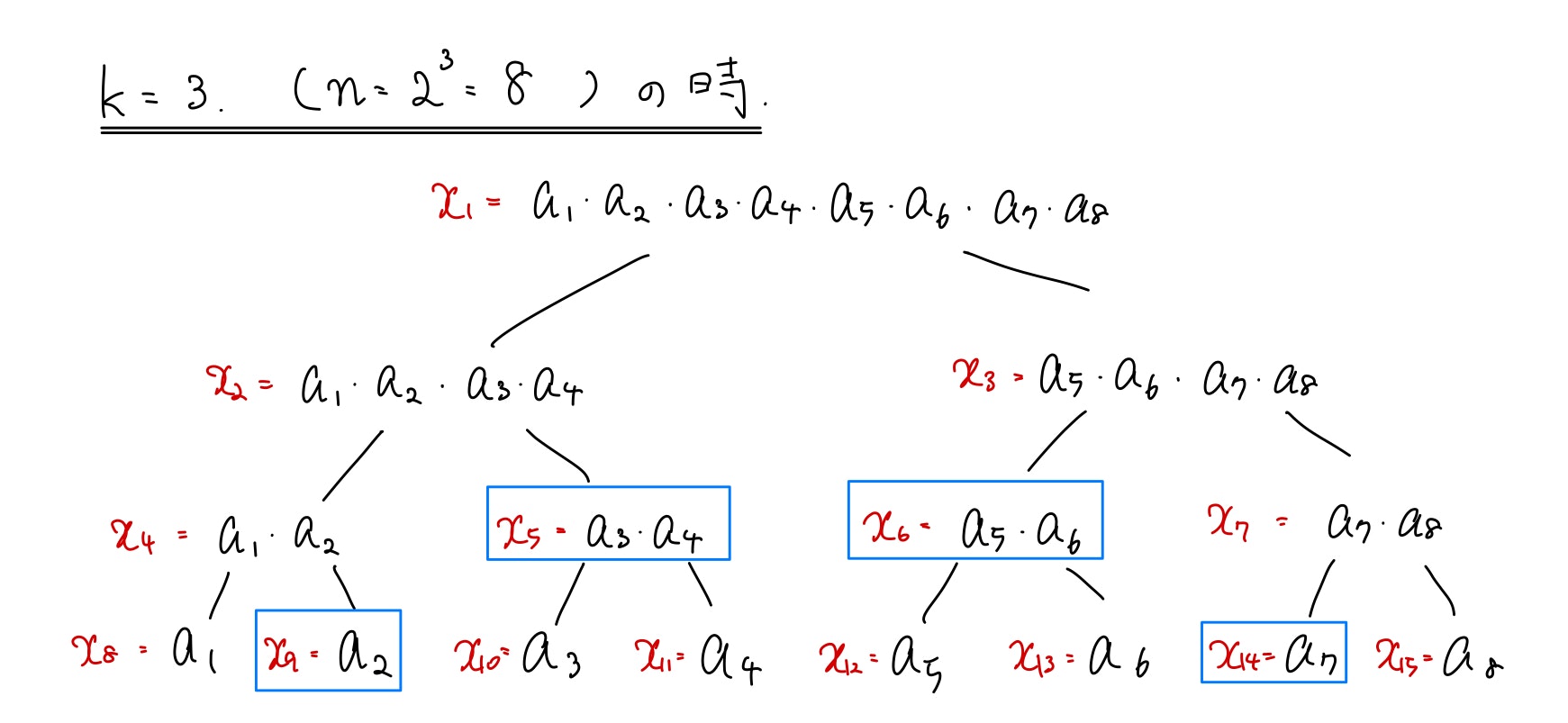
上の図で青い四角で囲んだものを見ていき、かけ合わせれば答えが求まります。計算量はこれも層の数だけ見ていけばよく、$O(\log n)$となります。
数列の個数が2のべき乗でない時は?
前項までの議論は、数列の項数が2のべき乗である時を考えていました。では、数列の個数が2のべき乗でない時はどうすればいいんでしょう?実は大体同じ手順で考えることができます。まず、完全2分木の葉の部分に数列をセットするわけなので、葉の個数は数列の項数より多くなければなりません。よって、$2^k\geq n$となるように$k$を設定し、完全2分木を作ります。
では余った部分には何を入れれば良いのでしょうか?実は単位元$e$を入れておけば矛盾なくセグメント木を作ることができます。試しに$n=5$の時を見てみましょう。
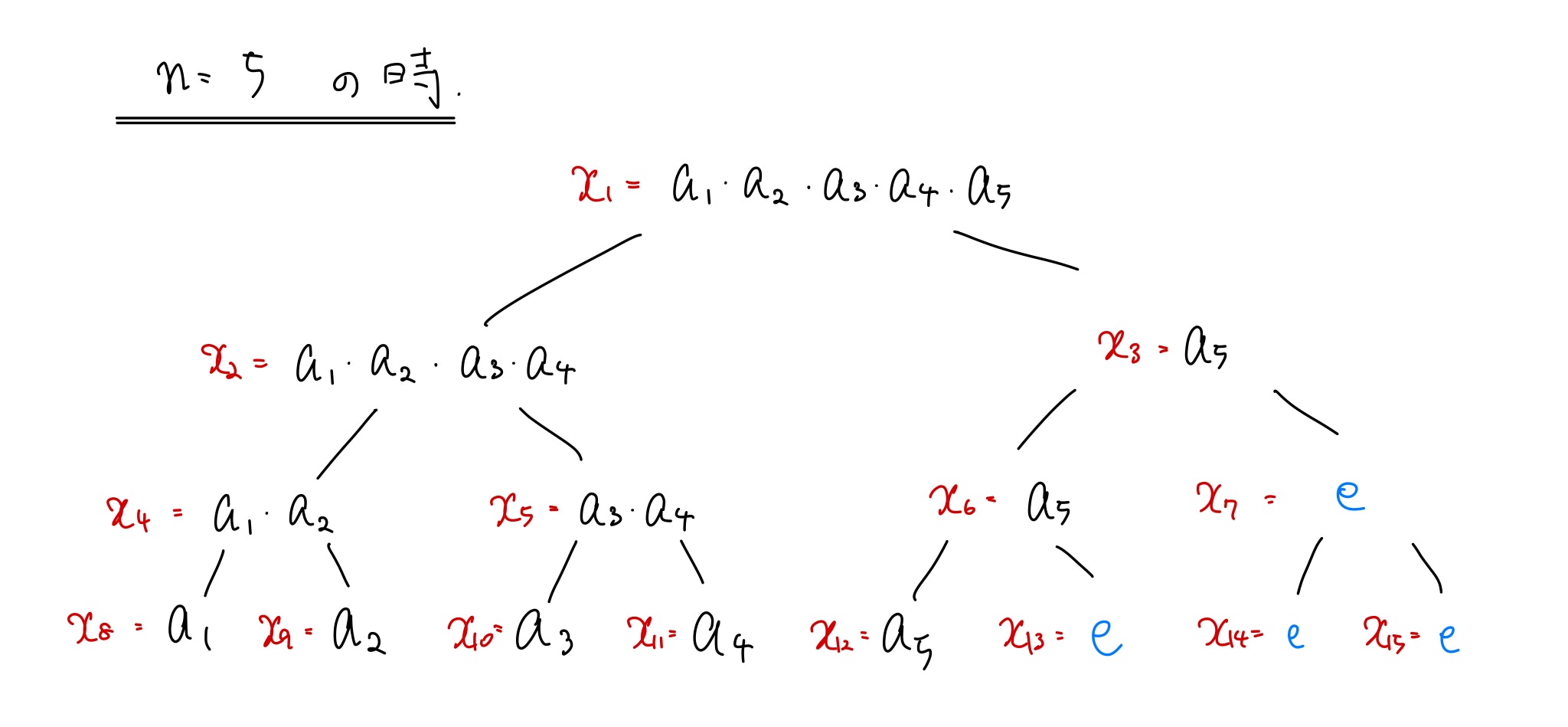
$x_8, ..., x_{12}$に数列$a$を入れ、余った$x_{13}, x_{14}, x_{15}$には単位元$e$を入れておきます。
$$2^2<6, 2^3\geq 6$$
ですから、$k=3$として完全2分木を作りました。単位元は作用する際に値に影響を与えないため、上図のように矛盾なく木構造を作ることが可能です。
いざ実装
ここからが地獄でした。私が実装に不慣れというのも多分にあるのですが、一番面倒だったのは添え字の管理でした。
とりあえず手順としては
- $2^k \geq n$となる最小のkを求め、2分木をモノイドの単位元で初期化する
- 葉の部分に数列を入れ、親ノードを逐次求めていく
- 更新メソッドの実装
- 区間の総積を求めるメソッドの実装
という感じです。1つ1つやっていきましょう。
1. 2分木の初期化
変数が少し変わっていてアレですが、$size$が元の数列の項数、$n$が葉の個数です。$n\geq size$となるまで$n$に$2$をかけていっています。
n = 1
while n < size:
n *= 2
node = [0]*(2*n-1)
2. 葉の部分に数列を入れ、親ノードをもとめる
2分木の葉の番号は$n-1, ..., 2n-2$になっています。なので、この頭から$size$個の部分に考える数列を代入していきます。
次に親ノードを求めていくのですが、ここで注意すべきことがあります。それは、2分木の最初の項の番号が$0$であることです。これにより親ノードと子ノードの関係は
$$x_i = x_{2i+1}・x_{2i+2}$$
になっています($i=0, 1, ..., n-2$)。関係がわからなくなった時には、具体的な項数で図を書いてみるとわかり易いです。
for i in range(size):
node[i+n-1] = a[i]
for i in range(n-2, -1, -1):
node[i] = node[2*i+1] ^ node[2*i+2]
3. 更新メソッドの実装
$a_i(i=0, 1, ..., n-1)$を更新する際、2分木中では番号$i+n-1$の項が更新されます。そこから親ノードの更新を逐次行っていくわけですが、番号$i$の親ノードは、$\frac{n-1}{2}$となります(切り捨て割り算)。この親ノードへの遷移に関しても、2分木の番号が$1$から始まる時とは異なるため、注意が必要です。
def update(i, x):
i += n-1
node[i] = x
while i > 0:
i = (i-1)//2
node[i] = node[2*i+1] ^ node[2*i+2]
4. 区間の総積を求めるメソッドの実装
$[L,R)$の区間に対して総積を求めることを考えましょう。まず$L,R$を2分木の葉の番号に直すために$n-1$を加えます。
ここで$L$の位置に着目します。このノードが、二股に分かれたうちの右側だった場合(総積について説明した画像における$a_2$みたいな場合)、そのノードを保存して1つ右のノードに移ります($L$に$1$を加える)。$R$についても同様な処理を行いますが、$L$と$R$で閉区間と開区間が異なるため、$R$に関してはノードの移動がありません。
こののち$L,R$共に親ノードに上がり、この操作を$L,R$が一致するまで行い、保存していったノードの値をすべてかけ合わせれば答えとなります。
def fold(L, R):
L += n-1
R += n-1
vL = 0
vR = 0
while R > L:
if L % 2 == 0:
vL ^= node[L]
L += 1
if R % 2 == 0:
vR ^= node[R-1]
L = (L-1)//2
R = (R-1)//2
return (vL^vR)
これでなんとかACすることができました。やったー!
反省
- 新しい知識が増えてよかった。
- 番号管理を適当にやっていたら無限にバグを吐いたので反省。冷静に図に書き出してゆっくり実装すれば問題なさそう。
- クラスをよく理解していないけど、まとめられると今後類題が出た時に楽っぽそう。どうせしばらくは競プロやるし、ライブラリ整備とかやろうかな。
- 記事を書きながらポテチ食べてたら上顎に刺さって痛い。