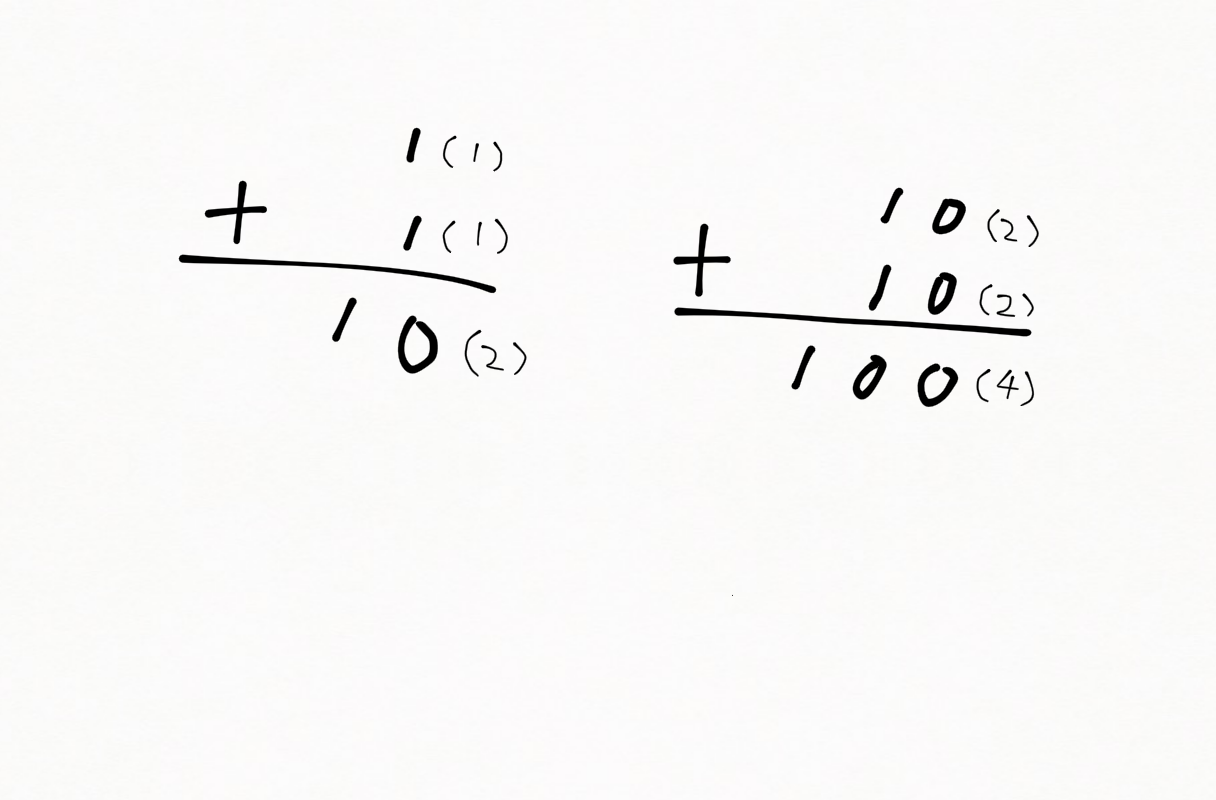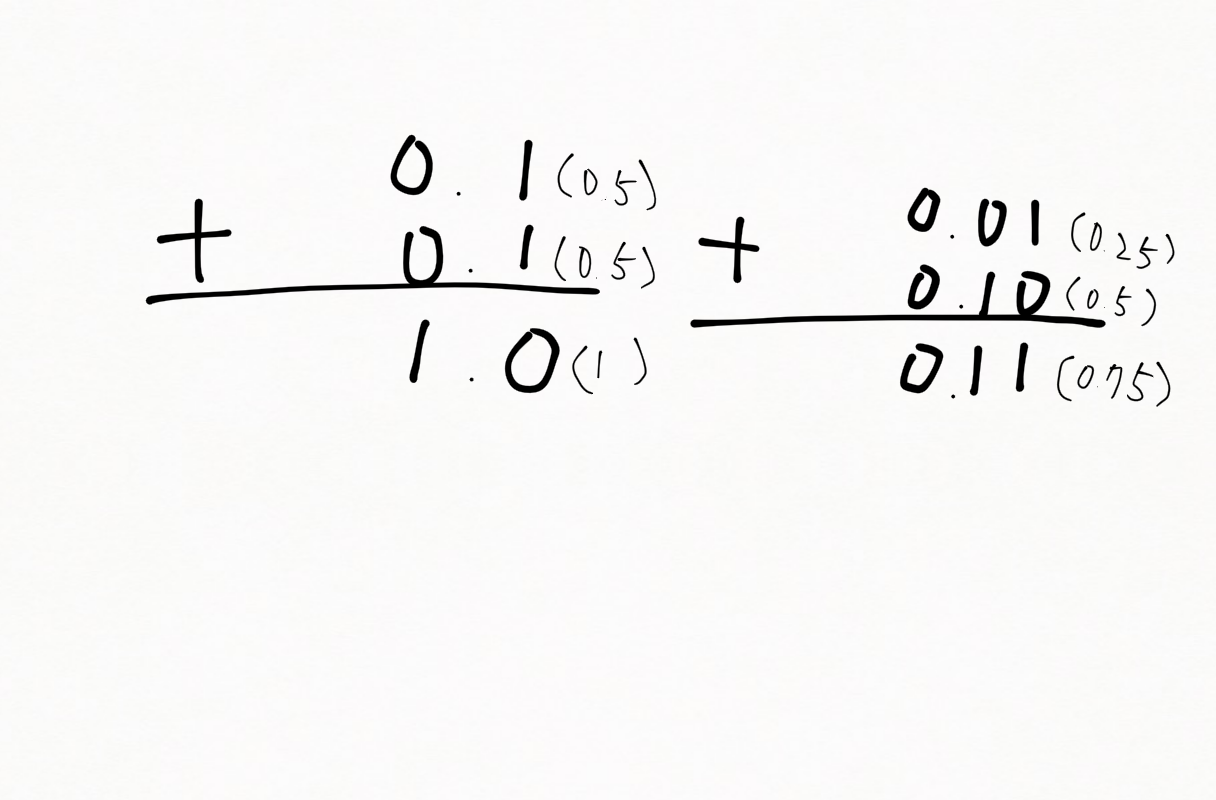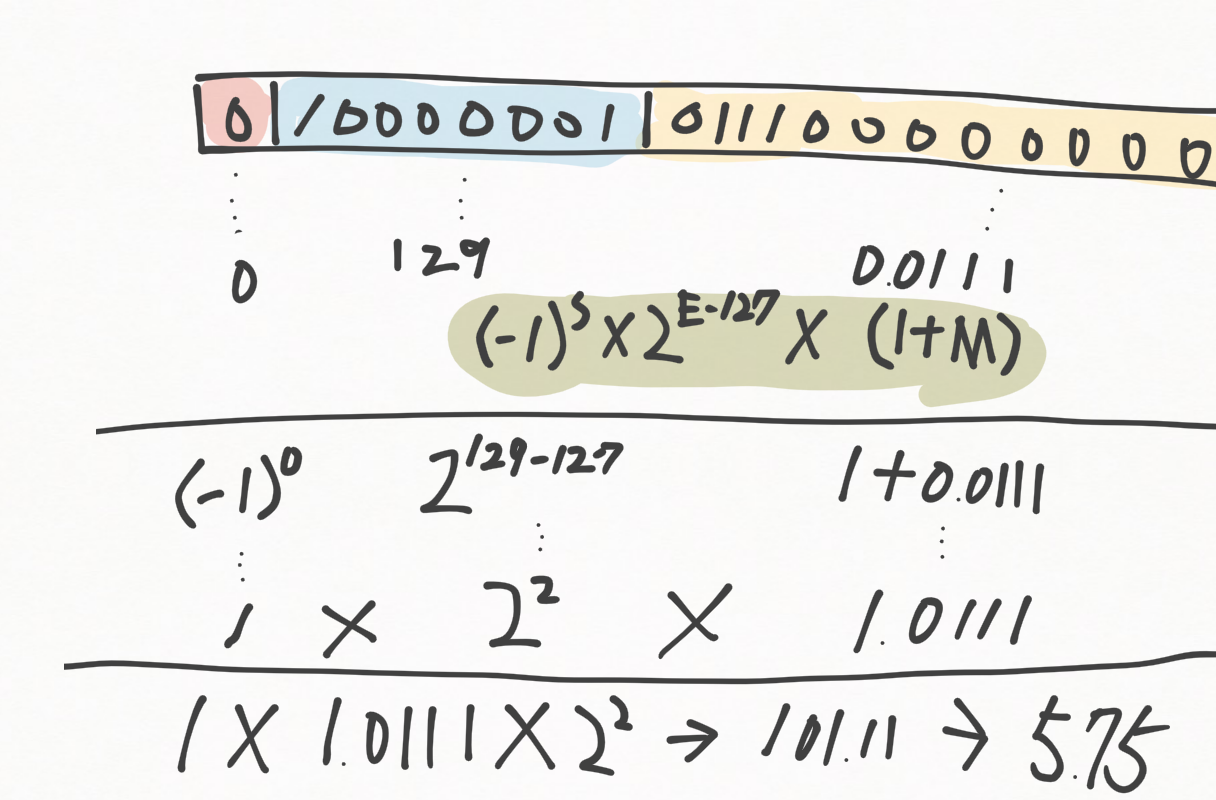Fringe81 アドベントカレンダー2017の14日目ですね。
近頃は覚えたことを復習するために、娘が話している体で一人二役の会話をしています。
娘は今日でちょうど生後4ヶ月になりました。
傍から見たら延々独り言でヤヴァいやつですが、自宅でしかやってないので今のところ大丈夫です。
そんなわけで、最近ちゃんと知ったIEEE754の浮動小数（0.1を10回足すと1にならないやつ）について娘と会話してみたいと思います。
説明を分かりやすくするため細かい説明などは端折っているのでご了承ください。
「おとーしゃんおとーしゃん。コンピュータはどうやって計算してるんでしか？」
「どうしたななちゃん。いくらなんでも唐突だね。」
「気になって眠れないでし！早く聞きたいでし！」
「じゃあまず、全てはON/OFFで表現しているのは知っているかな？」
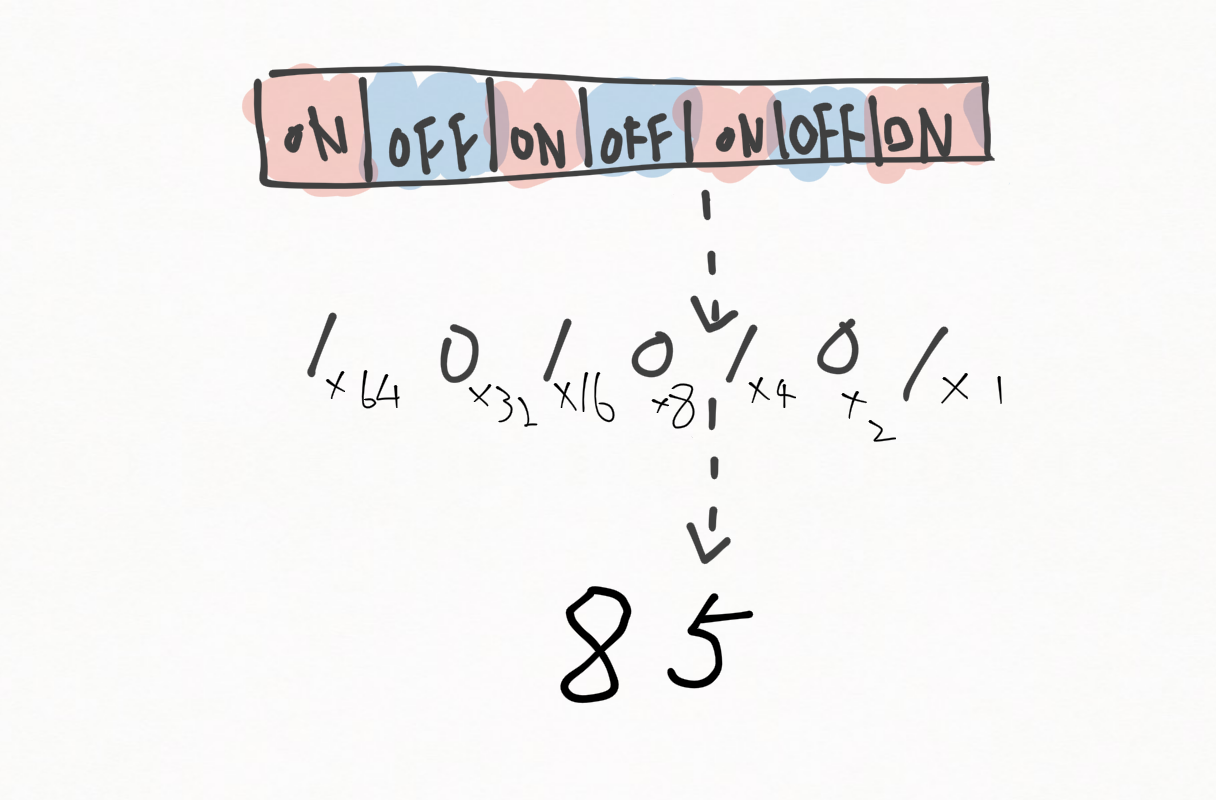
「それは知ってるでし～。大体こんなイメージでしよね？」
「その通り！これなら0と1だけ使ってどんな数字でも表せるね！というか2進数の変換も知ってるなんてすごいね！」
「たしかに大きい数字は困らないでしけど、0より小さい数字や1の半分はどうやって表すでしか？」
「よし、じゃあこれからななちゃんの気になる数字について説明していこうか。」
「コンピュータの種類やプログラムによって全部が同じということはないけど、最小でも数字を8桁の2進数で表現しているよ。」
「そうなんでしか。」
「もっと大きい数字を扱うときは16個、32個と8の倍数の桁で表現するよ。」
「そうなんでしか。」
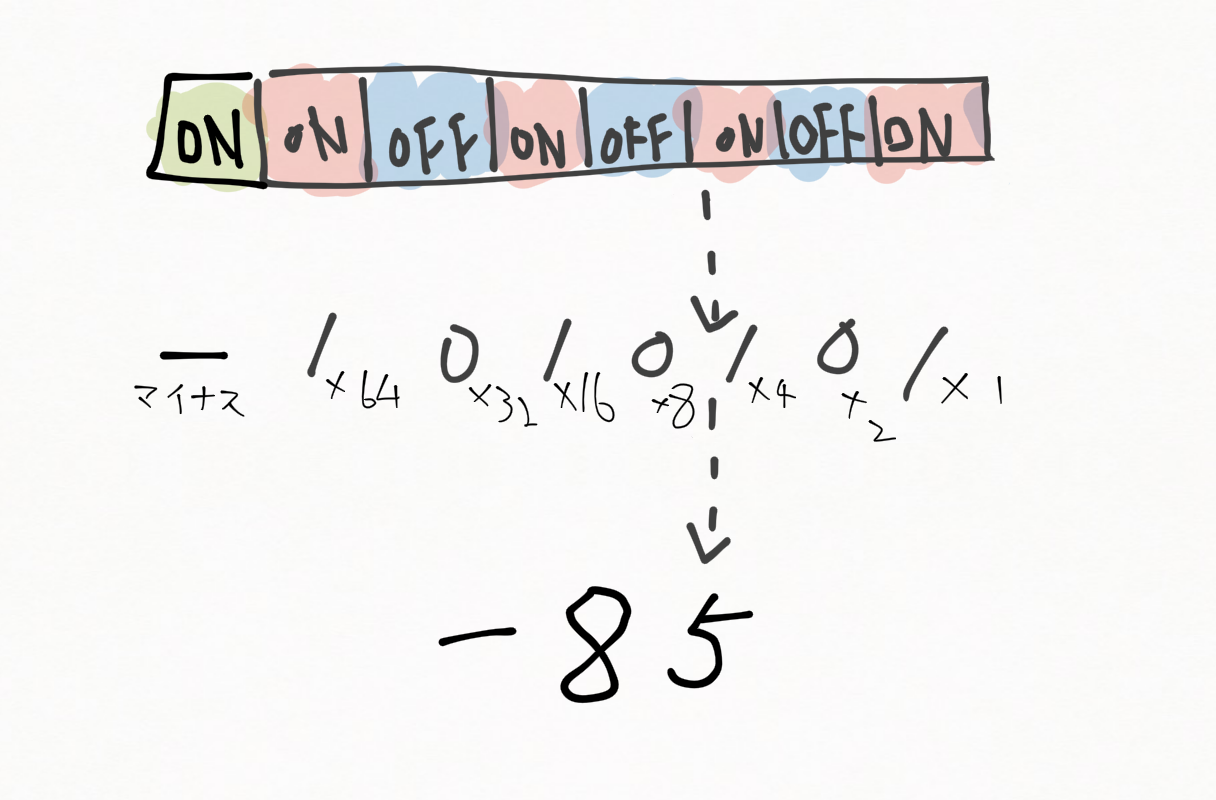
「そして、0より小さいマイナスの数字を表すときには1番左の桁をプラスかマイナスとして使うんだ。符号あり整数という言い方をしていて、大体こんな感じだね。」
「そうなんでしね～」
「ななちゃん反応が薄いね。おとうさん張り合いがないよ。」
「このあたりは知ってたでし。早く浮動小数点数の話が聞きたいでし。」
「さっきは『1の半分』なんて言いながら浮動小数点数を知っていたのか。ななちゃんさすがだね。」
「1の半分である0.5を2進数で表現するとどうなるかな？」
「0と1だけ使うんでしよね？0.5の5や、1/2の2は使えないでしよね？うーん・・・どうするでしか？」
「じゃあ図で追ってみよう。」
「2進数で1と1を足し合わせると、桁が増えて10になるよね？」
「2進数の10は10進数の2だから合ってるでし。」
「2進数で10と10を足し合わせるとまた桁が増えて100になるけど、何か法則性がわかるかな？」
「2進数の100は10進数の4でしから・・・倍の数になると桁が増えるでしか？」
「その通り！ななちゃんは察しが良いね！説明しやすいよ。」
「100が4で1000が8でしから、おとーしゃんの言う通りでしね。」
「これを1より細かい数字で考えるとこんな感じになるね。」
「なるほどでし！0.1(2)と0.1(2)を足して1(2)になるんでしから、0.1(2)は1(2)の半分、10進数の0.5になるでしね！」
「さらに0.01(2)は0.1(2)の半分で十進数で0.25と、どんどん細かい数字になっていくよ。」
「1の半分の0.5は分かったでし。じゃあ1の1/10はどうやって表すでしか？」
「実はこの方法だと1/2ならいいけど、1/10とかはおおよその数値でしか表現できないんだ。しかも桁も長くてキリがないんだ。」
「googleで調べたら、0.0001100110011001...ってなったでし！正確には出せないみたいでしね～」
「ななちゃん自分で答え調べちゃったんだね！お父さん用無しだよ！」
「2進数で小数を表現する方法は分かったでし。浮動小数点の表現はいつ出て来るでしか？」
「今からだよ。小数が出てくると0.00000101(2)だったり、桁数が多くなって見づらい事があるよね？」
「それは数えるのも面倒でし。」
「これを仮数部と指数部に分けた表現を浮動小数点表現と言うんだ。仮数部は数値で、指数部は桁を表していると考えればいいよ。」
「実際にはどんな風になるんでしか？」
「さっきの0.00000101(2)だったら、101(2)が仮数部で小数の8桁が指数部になるよ。ちょうどこんな感じだね。」
$0.00000101 = 101 × 2^{-8}$
「ひぇ～！ずいぶんと数えやすくなるでし！浮動小数点すごいでし！」
「そう！これならどんなに桁が多くても表すのが楽になるよね！」
「でも気になるでし！こんな感じでいくらでも表現できてややこしいでしよね？全部違う表現でも同じ数字でしよ？」
$101 × 2^{-8} = 10.1 × 2^{-7} = 1.01 × 2^{-6} = 0.101 × 2^{-5} ...$
「仮数部の小数点の位置と指数部の桁をいじれば同じ数字がいくらでも作れてややこしいでし。」
「実はIEEE754という規格で、仮数部は1.・・・とするという決まりがあるんだ。つまり、この表現が基本的なんだ。」
$1.01 × 2^{-6}$
「ほぇ～！あいとりぷるいー754さんはすごいでしね！これならみんなが同じ表現になるでしね。」
「ななちゃんIEEE知ってたんだね！もう教えることない気がするけどもうちょっとだけ続けるね！」
「IEEE754が規格ってことは、仮数部の桁以外にも決まり事があるでしか？」
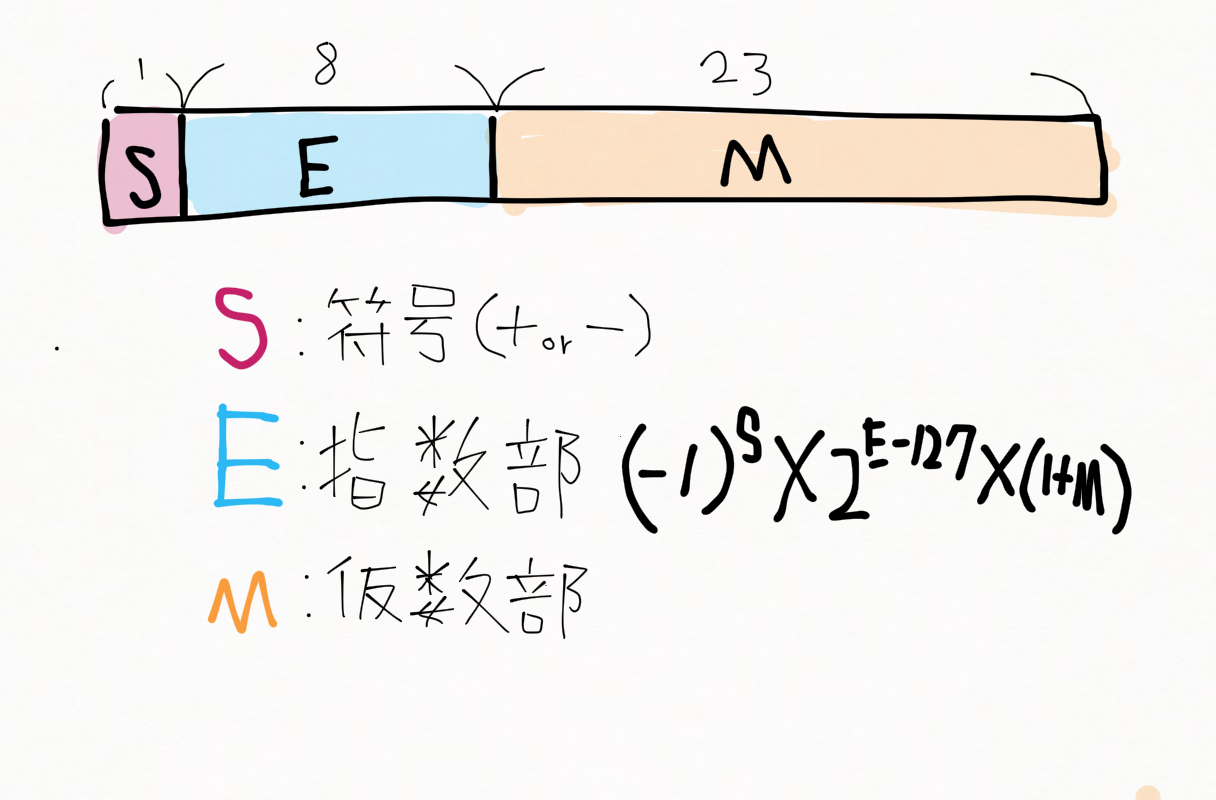
「もちろんあるよ！単精度と倍精度と呼ばれる形式があって、それぞれ32桁の2進数と64桁の2進数で表現するんだ。単精度だとこんな形式で表すよ。」
「初めの1桁が符号、2~9桁目が指数部、10~32桁目が仮数部だよ」
「字が汚すぎて式が頭に入ってこないでし・・・」
「ななちゃんなかなか辛辣だね！念のためもう一回書くね。」
$(-1)^{S} × 2^{E-127} × (1 + M)$
「頭に入ってこないのは字が汚いからだと思ったら、式がちょっとややこしいでしね。」
「ななちゃんは素直だね。そのまま素直な子に育って欲しいけどお父さん時々傷ついてるよ。」
「じゃあこの式で実際の数値を表現してみてほしいでし！」
「じゃあ試しに5.75を単精度形式の浮動小数点数にしてみよう！」
「してみるでし！」
「2進数にすると101.11になるね。」
「さらに仮数部と指数部に分けるでしね。」
「 $101.11 × 2^{0}$ にして分けたものを $1.0111 × 2^{2}$ の形式にするんだったね。」
「ここまでヒョイっと来たでしね。これで、さっきの式に当てはめてみるでし！」
「だいたいこんな感じだね！指数部の0は32桁までずっと続くよ。」
「ちょっと待つでし！なんで127足したり1引いたりしてるでしか！納得行かないでしよ！」
「さっきの式 $(-1)^{S} × 2^{E-127} × (1 + M)$ で、$E-127$したり$1+M$としてたよね？だから値を格納した状態では逆の計算をしてあげないといけないんだ。」
「そういうもんなんでしか…？まぁいいでしけど。」
「お父さんもなぜこうしたか経緯は知らないけど、気になるなら調べてみようね！」
「いいでし！気にならないでし！説明を続けるでし！」
「ななちゃんそういうとこあるよね！お父さんにそっくりだ！」
「じゃあ実際に単精度浮動小数点数の2進数を10進数に変換してみてほしいでし！」
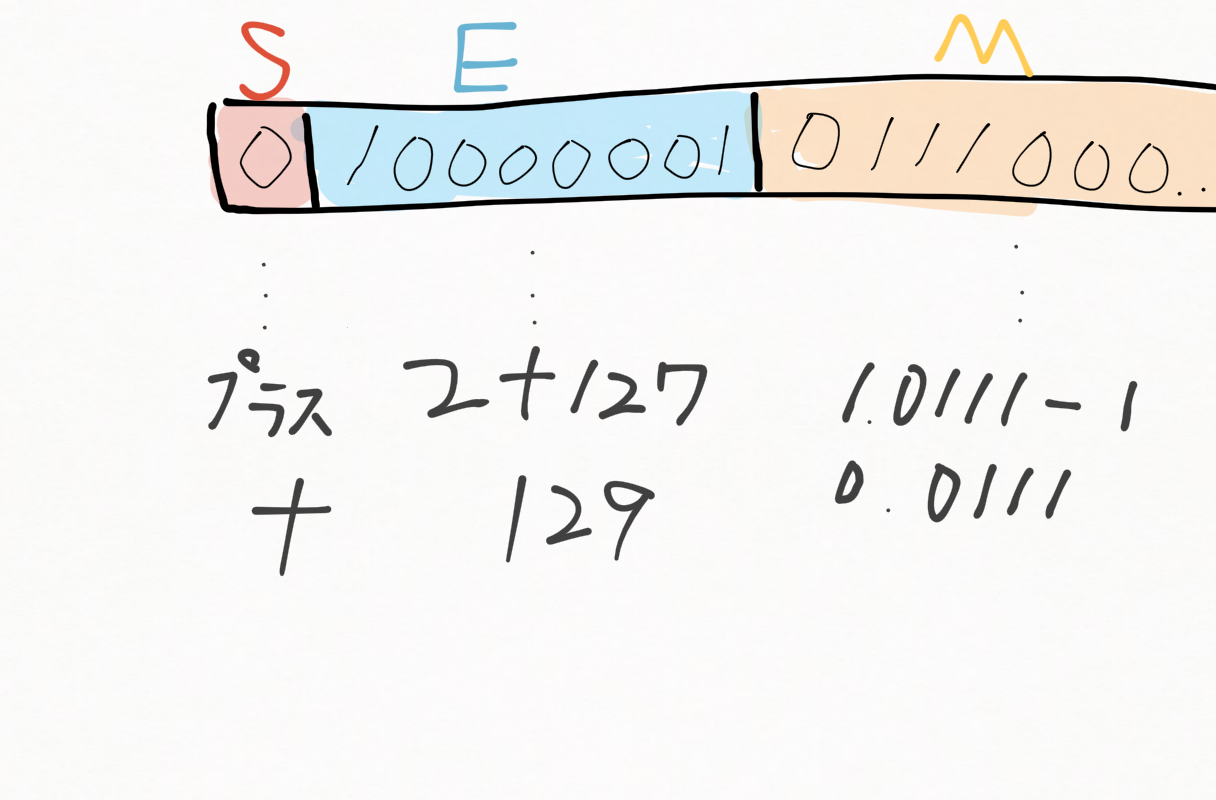
「01000000101110000000000000000000を5.75に変換してみるよ！」
「さすがに32桁はくどいでしね～」
「おぉ！なんかそれっぽい結果になったでしね！余白ギリギリまで書いてて感心でし！」
「そう！頑張って書いたよ！納得できたみたいでよかったよ。」
「ところで、0.1を10回足しても1にならないって話を聞いたことがあるんでしが、浮動小数点数が関わってるんでしか？」
「そうだよ。さっき0.1を浮動小数点数にした時、0.0001100110011001...となって正確には表せないという話が出たよね？正確じゃないもの同士を足していったらどんどん誤差が出てくるんだ。」
「そういうのをいわゆる用語で～？」
「情報落ちや、桁落ちっていうんだ。ななちゃんやっぱ知ってるみたいだね。それぞれの説明はしなくても良さそうだね！」
「0.1を10回足しても1にならないのは桁落ちしたせいでしか？」
「そういうことだね。0.1を単精度形式で表現するとわかるよ。」
「0.1を単精度で表現すると、実は0.0999999977648252になってしまうでし！」
「そう。精度の限界だね。0.1を10回足せば1になるけど、本当は0.1よりわずかに小さい数字同士を足していたんだ。」
「0.1よりわずかに小さい数字同士を足したら更に桁落ちして、徐々に誤差が大きくなっていたということなんでしね～。」
「ななちゃん、また賢くなったね！」
「やったでし！今日はこのへんで終わりにするでし！」
どうだったでしょうか。
将来娘がこの話を理解してくれるのかはわかりませんが、こんな感じで話すと復習になっていいかと思います。
Fringe81では30代前半のお父さんエンジニアが増えてきており、Slackでもお父さんチャンネルなどがあります。
これからの家庭の未来をつくるお父さんエンジニアの方々、我々と一緒に地球の未来も作ってみませんか？
もしよろしければ弊社サイトへ遊びに来てみてください。実際に会社へ見に来ても大丈夫ですよ。
「待ってるでしよ！」
続き書きました。