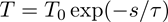はじめまして。株式会社Qunasysインターンの髙木です。
今回紹介する論文は、NISQ上で量子ビット(qubit)を割り当てる方法を新たに考案したものです。
(NISQ … Noisy-Intermediate Scale Quantum computerの略。現在世界中で開発が進む、誤り訂正機能を持たない量子コンピューターのこと。)
論文のタイトルとURL
Qubit Allocation for Noisy Intermediate-Scale Quantum Computers
https://arxiv.org/abs/1810.08291
著者
Will Finigan, Michael Cubeddu, Thomas Lively, Johannes Flick, and Prineha Narang
ハーバード大の方々。Lively氏はGoogleにも所属していますが、この論文はGoogleとは関係がないそうです。
ポイントは?
昨今、GoogleやIBMなど世界中の企業が(主にハード面で)量子ビットの研究を盛んに行っていますが、古典コンピュータと同じく、量子ビットにも役割を与えなければただの箱です。プログラムを実行する過程で、どのビットに初期化・演算を行い、結果を記録するのか、などの役割を割り当てる作業をコンパイルといいます。
今回の論文では、プログラム上の量子ビット(logical qubit)の役割を、現実の量子ビット(physical qubit)に精度よく振り分ける問題(qubit allocation問題)に対して、新たなアルゴリズムを開発しました。
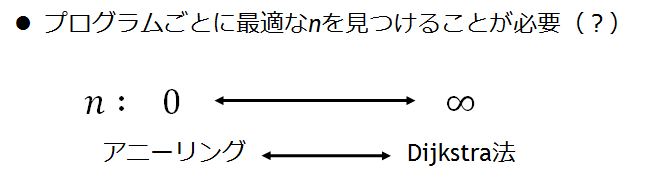
特徴としては、Dijkstra(ダイクストラ)法とアニーリングを結び付けて考えたことが挙げられます。
要するに…
量子コンピュータ用の新しいコンパイル方法を考えた
ということです。
先行研究と比べて何がすごい?
これまでプログラム上の量子ビットを配置するとき、ビット間のエラー率はほぼ全て同じものとして考えていました。そのため、qubit allocation問題に対しては"ゲートの数をいかにして減らすか"という点に主に焦点がおかれていました(ゲートを通るときはエラーが生じやすいので)。
しかし当然ながら、量子の世界(μmスケール)ではそんなに正確な性能をもつ素子は作ることができず、エラー率にもばらつきが生じます。そこで今回の論文では、エラー率のばらつきを考慮した新しい配置方法を考えました。
例
画像はこちらより引用
左図のようなシンプルな量子回路を考えます。A ~ Eはphysical qubit, 各qubit間の数字はfidelityを表しています。合計fidelityは積で表されるとします。
さて、3つの連結したqubit間で情報をやり取りしたい状況を考えます。これまでは各qubit間のfidelityは全て同じとして考えていたので、どの連結する3qubitでも同じ合計fidelityが得られるとしていました。しかし、実際は各qubit間のfidelityは同じものとは限りません。左図のような回路では、全ての隣り合う3qubitの組み合わせのうち、合計fidelityが最も高くなる組み合わせはD-E-Aとなります(右図)。このような「与えられたqubitの配列上で、合計fidelityが最も高くなるようなqubitの組み合わせを(qubit間のfidelityはそれぞれ異なるとして)求める」考え方をVariation-aware Qubit Allocation(VQA)と呼びます。
今回の論文では、VQA方式の新しい量子コンパイラを開発し、既存のコンパイラと比較しました。
また論文には出てこないのですが、関連する話題として、VQMという考え方があります。同じ回路で、Aの情報をCへと伝達させたい場合を考えます。合計fidelityが高くなるような伝達ルートを考えるとき、これまでは各qubit間のfidelityは全て同じとし、ゲート数の少なさを第一に考えていたので、最も合計fidelityが高くなるルートはA-B-Cとしていました。
しかし、左図のような回路であった場合、A-E-D-Cルートの方が、ゲート数が多くても合計fidelityは大きくなります(中表)。このような「与えられた2qubit間の合計fidelityが最も高くなるようなルートを(qubit間のfidelityはそれぞれ異なるとして)求める」考え方をVariation-aware Qubit Mapping(VQM)と呼びます。
技術の手法や肝は?
提案されたアルゴリズムは、Dijkstra法とアニーリングの考え方を組み合わせています。
Dijkstra法
簡単に言えば、スタート地点を最適解とし、その近傍に値がもっと良い解があればそれを最適解として更新していく方法です。
他の探索法と比べ、シンプルで計算量が少ないというメリットがありますが、local minimumにハマってしまう可能性も高いです。
例
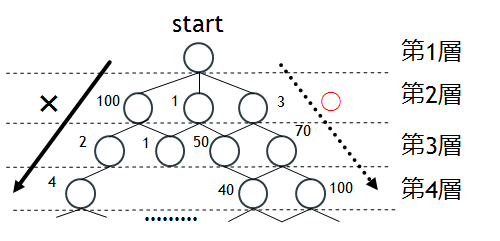
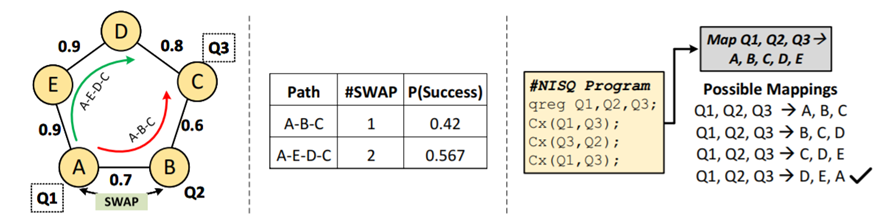
上図のような樹形図を考えます。第m層の○はm個のqubitの割り当てパターンを、○のそばの数字はその割り当てのfidelityを表しています。なお、回路全体のfidelityは、わかりやすくするため和で表されるものとします(積になっても考え方は変わりません)。
第2層の○のうち最もfidelityが高いのは100です。そのためDijkstra法は100を最適解とし、100から伸びる割り当てのみを探します。しかし、100から伸びるのは第3層の○のうち比較的小さい2,1のみです。仕方がないので2を選びます。さらに第4層でも候補は4しかありません。同じ層には40や100もあるにもかかわらず。このようにDijkstra法では一度local minimumにハマってしまうとなかなか抜け出せないというデメリットがあります。
アニーリング
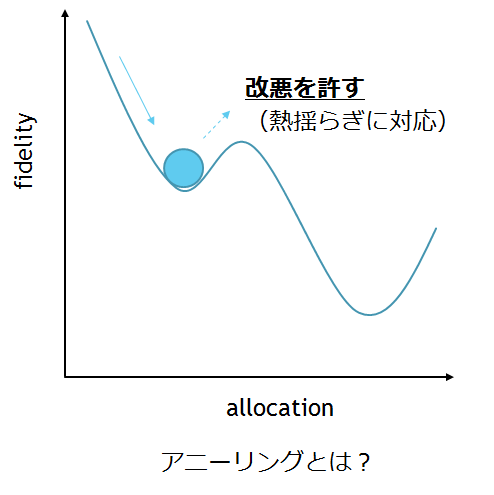
そこで導入するのがアニーリングの考え方です。アニーリング(焼きなまし法)はもともと、ポテンシャルが熱揺らぎによってlocal minimumを抜け出し、冷めるころにはglobal minimumに落ち着く、という統計力学の現象を応用した局所探索法です。この現象によって、熱く液状になった金属は、冷めるとしばしば規則正しく並んだ結晶を作ります。
アニーリングでは、解候補が今の状態より悪くても、改悪を許します。この改悪が熱揺らぎに対応し、改悪を起こす確率は(パラメータ化された)温度に依存します。(温度が低くなる=試行回数が増える=改悪確率は減る、ということ)
hybrid algorithm
Dijkstra法とアニーリングを組み合わせたものが、今回開発されたhybrid algorithmで、Dijkstra法n回につき、1回アニーリング的な改悪を許します。
例として先ほどの樹形図で、n=3のときを考えます。
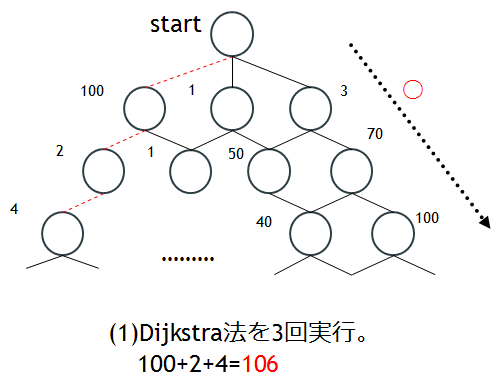
まずstartから一番大きいfidelityは100なので、100へと移動します。同じように移動先で大きいfidelityを選んでいくと、3回のDijkstra法で4の○へと移動します。ここまでのfidelityは
100+2+4=106
となります。
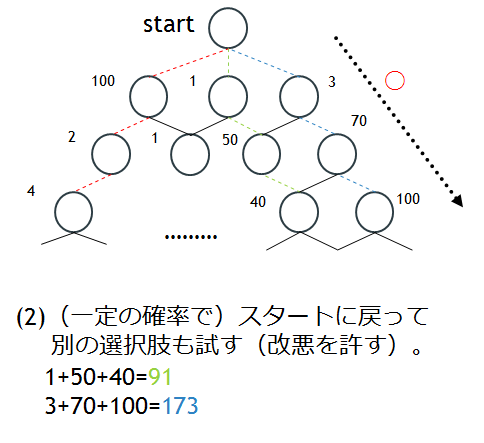
3回Dijkstra法を実行した後は再びstartまで戻り、他の選択肢も同じように3層分まで試してみて、fidelityを計算します。
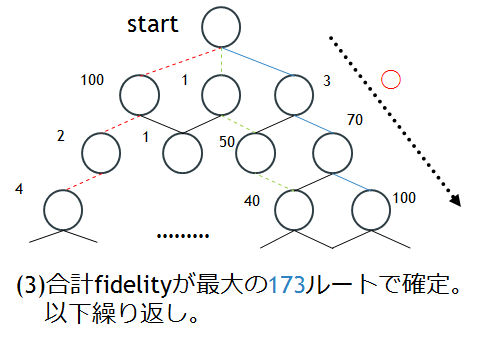
こうして得られた合計fidelityが最大のルートを最適解として確定します。以下(1)~(3)を繰り返します。Dijkstra法のみの時とは異なり、100 → 2 → 4ルートを避けることができました。
hybrid algorithmのメリット、デメリットは
○ local minimumにハマりにくくなる
○ 解の候補を減らせる
✖ nが小さいとやっぱりlocal minimumにハマる(ex:100 → 2 → 4ルートの先に最適解があったら…)
このアイデアはうまくいく?
(図は論文より抜粋)
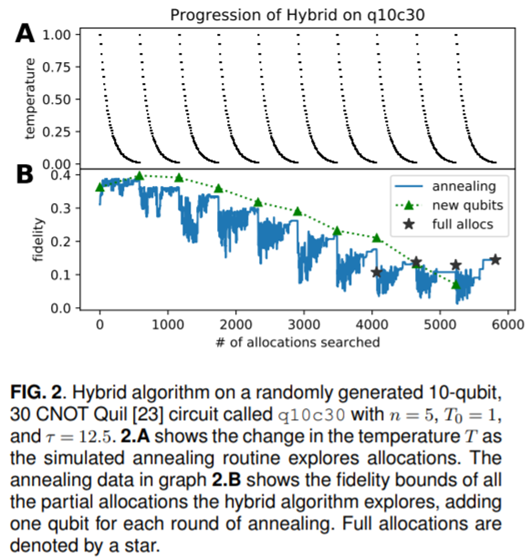
実際に30個のCNOTゲート上でhybrid algorithmを使った結果です。
始め1個のqubitからスタートし、fidelityが収束したところ(△)でqubitを1個ずつ増やしていくサイクルをqubitが10個になるまで続けました。
(T0 , τは定数)の関係があり、2.A図から探索回数が増えると各サイクルで確かに0に収束していることがわかります。また、それに伴い、各サイクルでfidelityが高い値に収束していることも確認できます。fidelityの収束値がqubitが増えるにつれて小さくなるのは、ノイズの影響が大きくなるためだと考えられます。
(図は論文より抜粋)
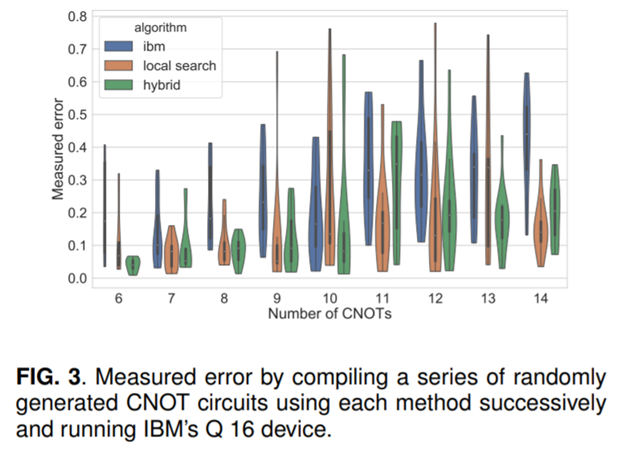
次に、CNOTのみからなるプログラムをランダムに作成し、3種類(IBM提供の既製、local serch(アニーリングなし)、hybrid)のコンパイラで実行しました。
- local searchは、ゲートの数が増えるほど、既製コンパイラよりも低いエラー率を示す
- hybridも既製よりは正確だが、local searchよりもエラー率にばらつきがある
ことがわかります。
議論はある?
樹形図のところでも書きましたが、hybrid algorithmでは、Dijkstra法とアニーリングのバランスを表すnが重要になってきます。nが大きければ改悪を許さず、Dijkstra法とほぼ同じ特色を持ち、逆に小さければ頻繁に改悪が起こり、アニーリングの特色(計算は正確だが時間がかかる)が強く表れるようになってきます。プログラムごとに最適なnを見つける方法が課題と言えそうです。