提出レポート(機械学習)
第1章:線形回帰モデル
・1点100文字以上で要点まとめ
線形回帰モデルは、回帰モデルの一つで、直線を用いることが特徴である。
曲線を用いるモデルは、非線形回帰と呼ぶ。
線形回帰モデルのパラメータは、
各入力それぞれに対応する重みづけ係数と、1つの切片から構成される。
それらは未知だが、教師データとの最小二乗法で推定できる。
汎化性能を確保するため、
教師データを、学習用データと検証用データとに分割し、
推定には学習用データだけを用いる。
最小二乗法の具体的な方法は、
平均二乗誤差を偏微分が0になるよう計算することで求められる。
・実装演習結果
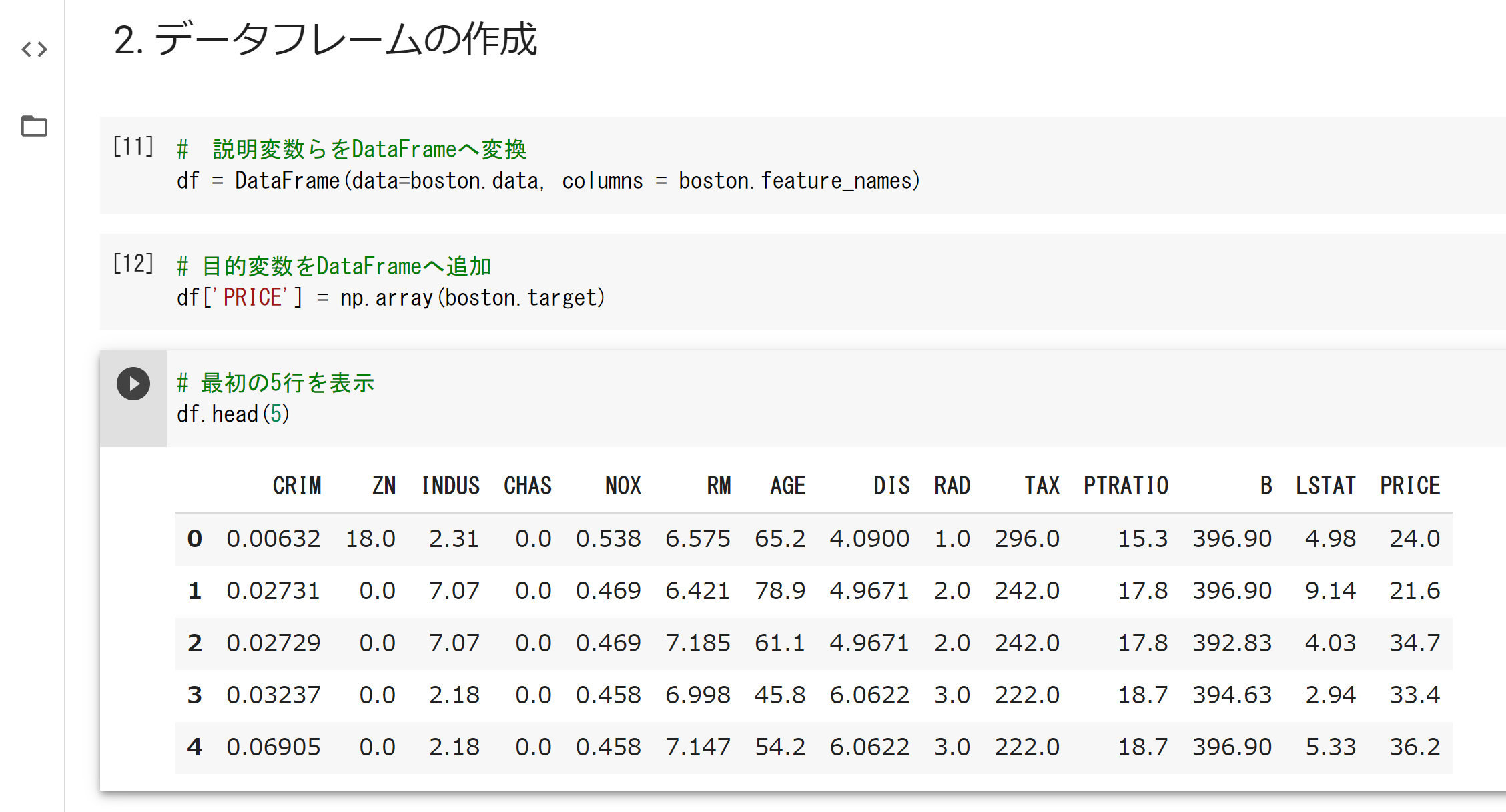
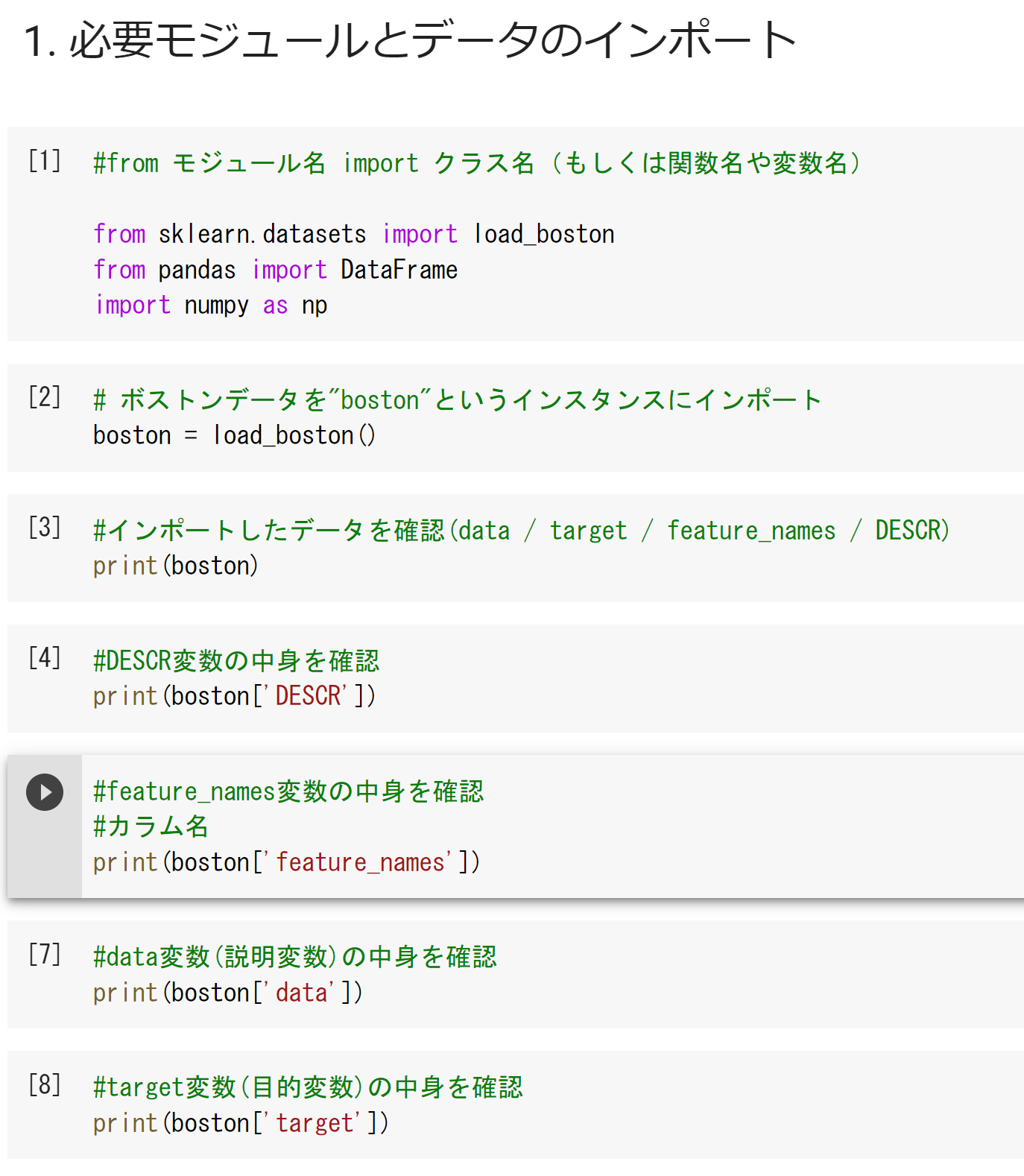
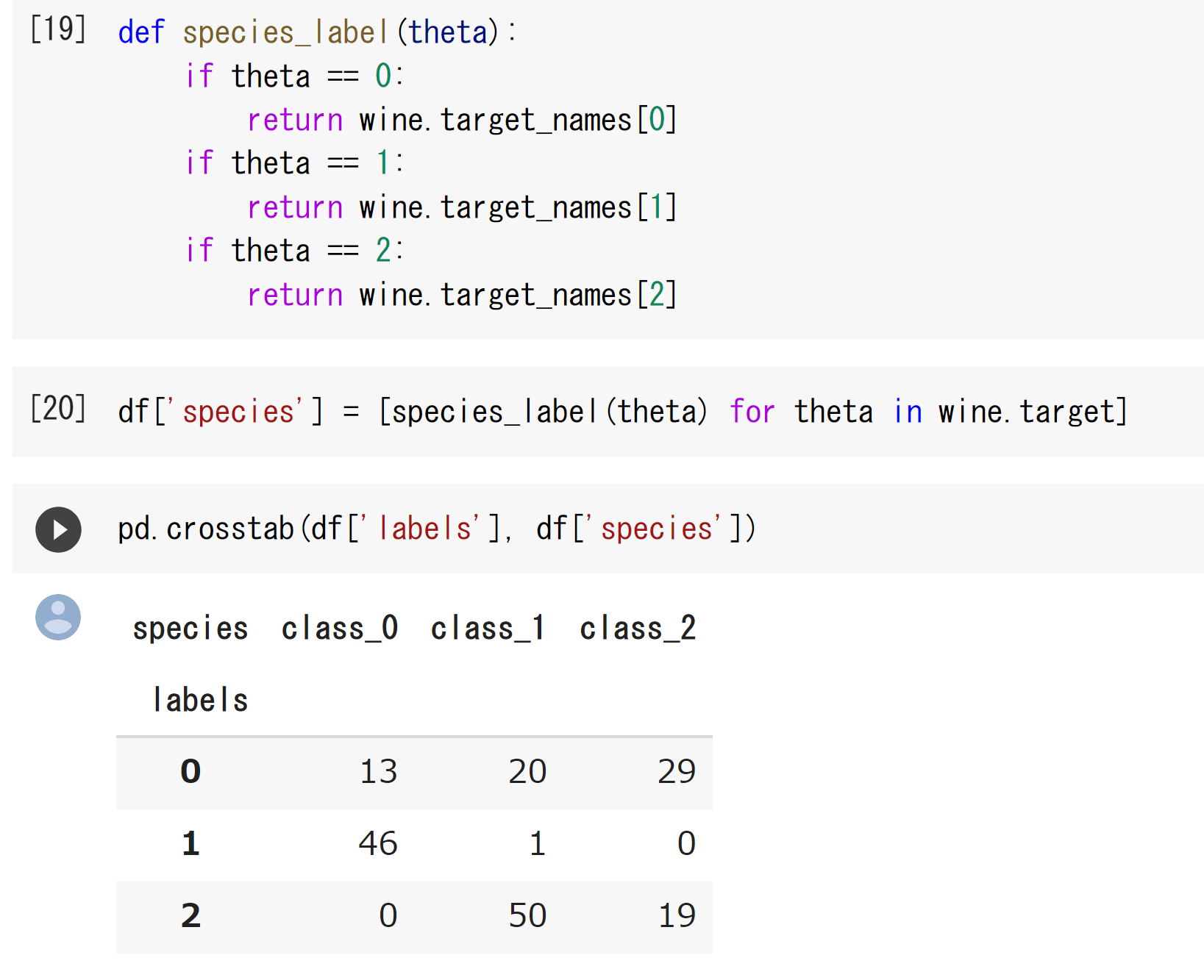
・bostonデータをカラム付きデータファイルに変換している
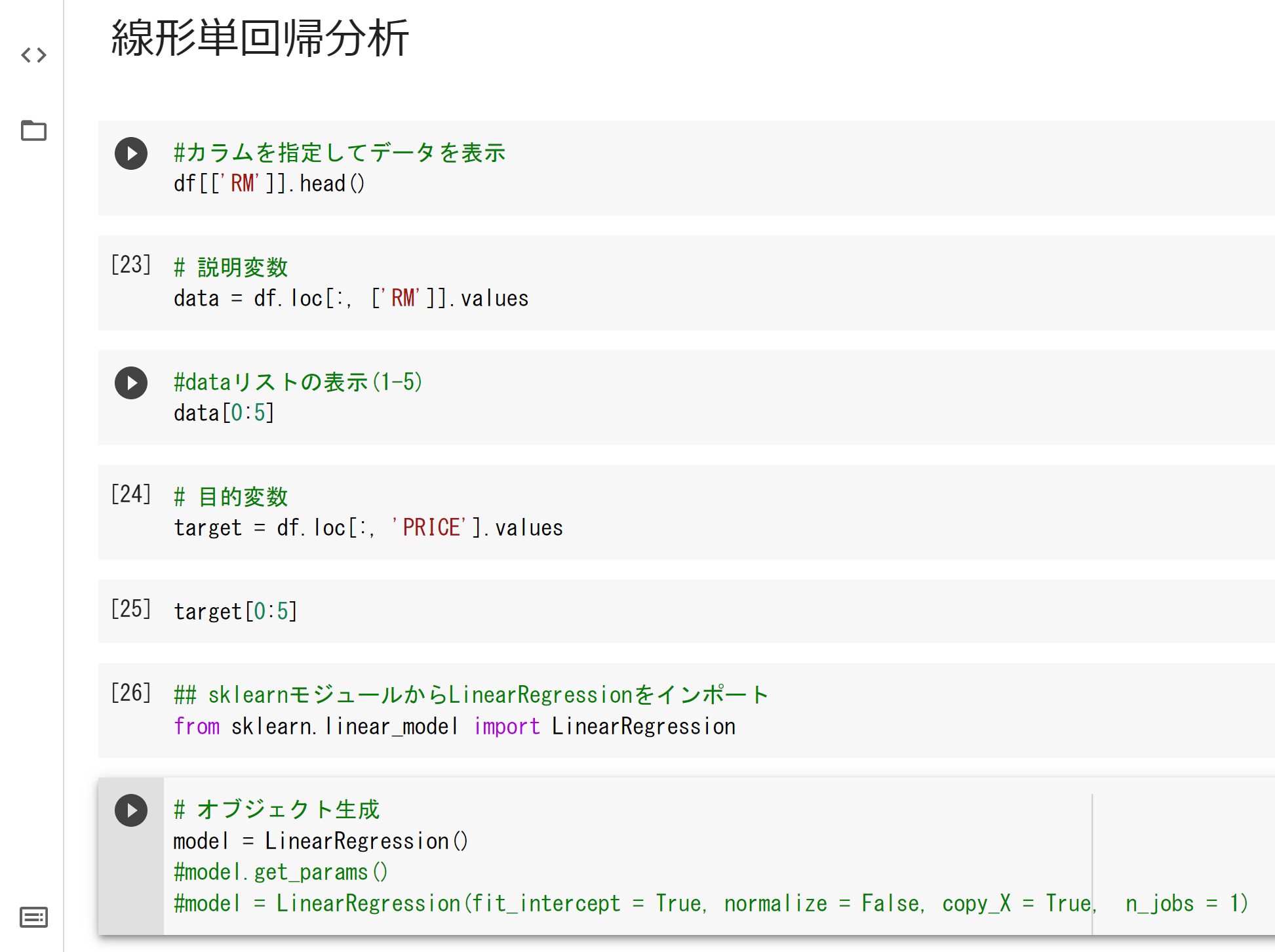
[23][25]が、「.head()」ではなく、「[0:5]」なのは、
データフレームではなく、np.array形式のため。
.head()が使えないことを確認済み
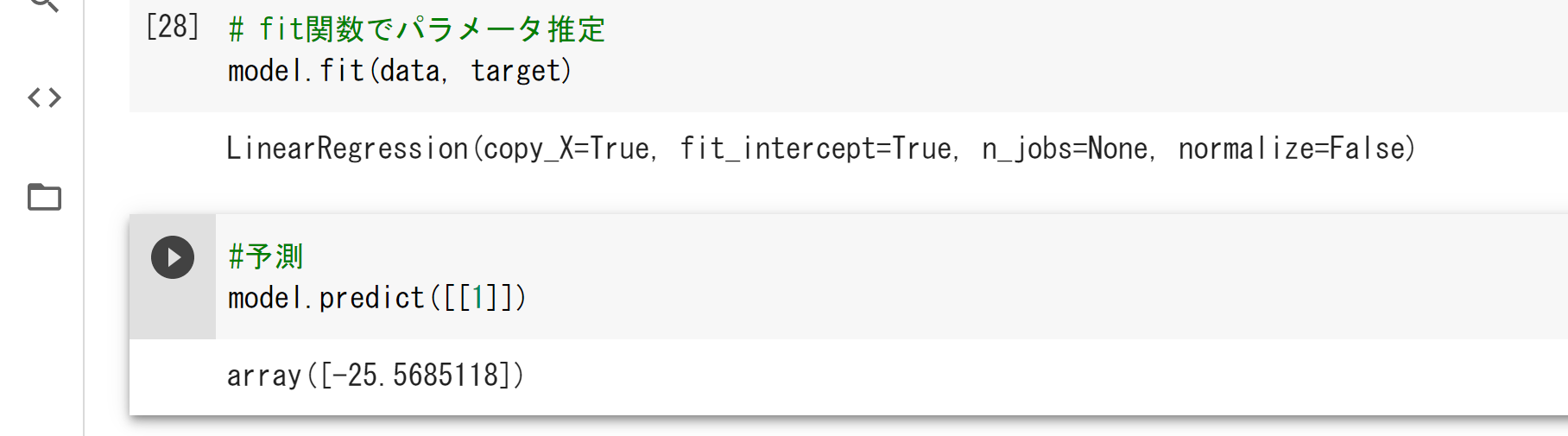
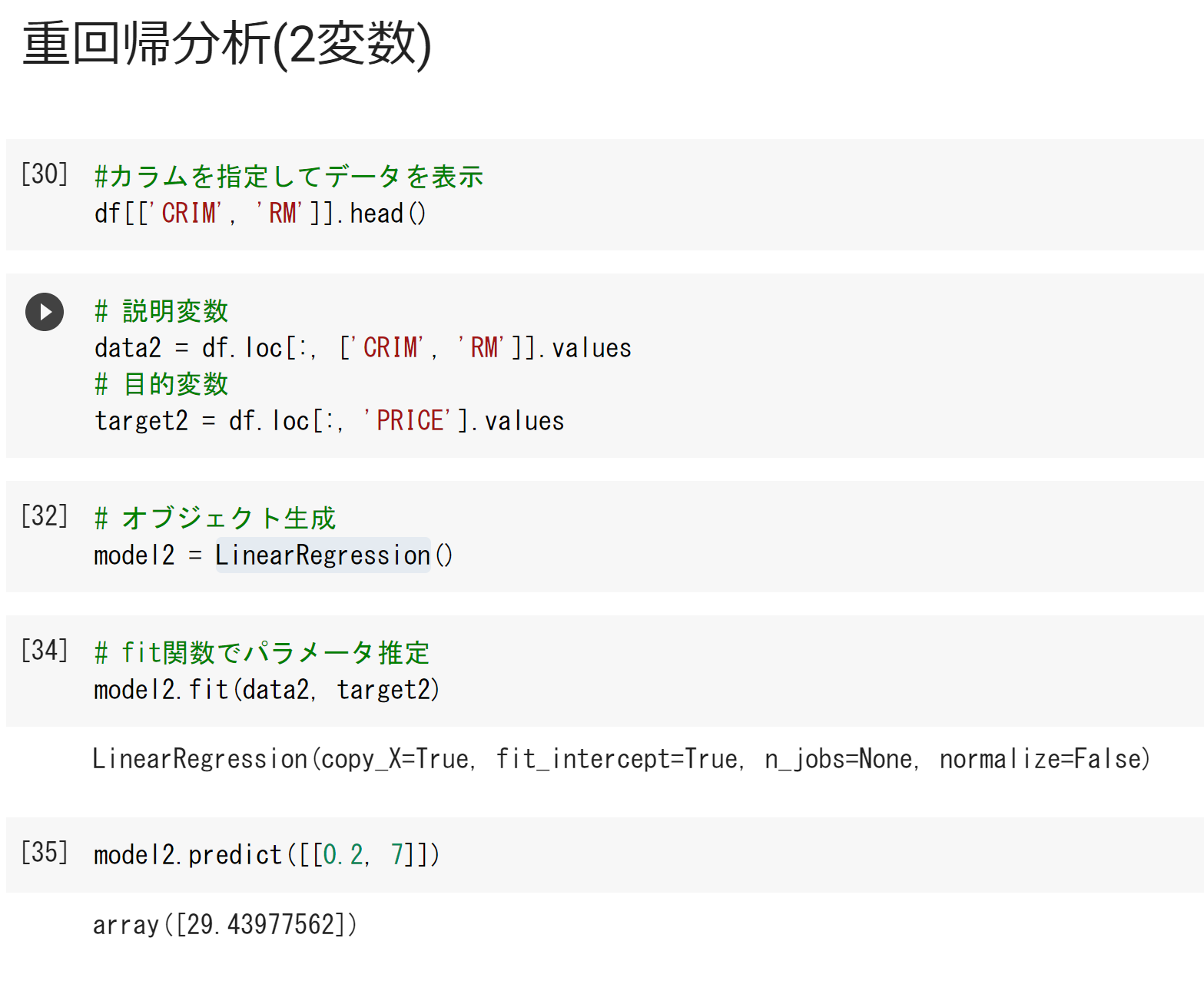
[28]の引数
copy=Xは、メモリでデータを複製するか
fit_interceptは、切片を含めるか否か
n_jobsは、計算に使用するジョブの数
normalizeは、入力データを正規化するか否か。
[27]で引数を省略しているので、全てデフォルト値が返されている
・確認テストなど考察結果
該当なし
・関連記事レポートによる加点
修了試験より
線形回帰の性質について
「モデルの表現力を下げたほうが良い場合がある」について考察
線形回帰であるから、表現力を下げることは、
入力データの次元削減または切片の削除と思われる。
一般的に次元削減をしないほうが、良い精度が得られるように思われた。
しかし、入力データ間に相関が高い組み合わせがある場合は、
片方を削除したほうが良い結果が得られる。
この場合が例外の一つなので「よい場合がある」が正解になると考えた。
第2章:非線形回帰モデル
・1点100文字以上で要点まとめ
非線形回帰は、線形回帰の説明変数部分に非線形関数(基底関数)を使用したもの。
基底関数には、多項式関数、ガウス型基底関数、スプライン関数/ Bスプライン関数が主に使用される。
学習データに対して、再現精度が得られないモデルを未学習という。
一方で、学習データに対してだけ、再現精度が高いモデルを過学習という。
過学習が起きると汎化性能が落ちる。
防止するため、正則化処理が行われる。
モデルの複雑さにペナルティを与える考えで、
ラッソ回帰・リッジ回帰が挙げられるれる。
汎化性能を測る方法として、
ホールドアウト法・クロスバリデーションが挙げられる。
・実装演習結果
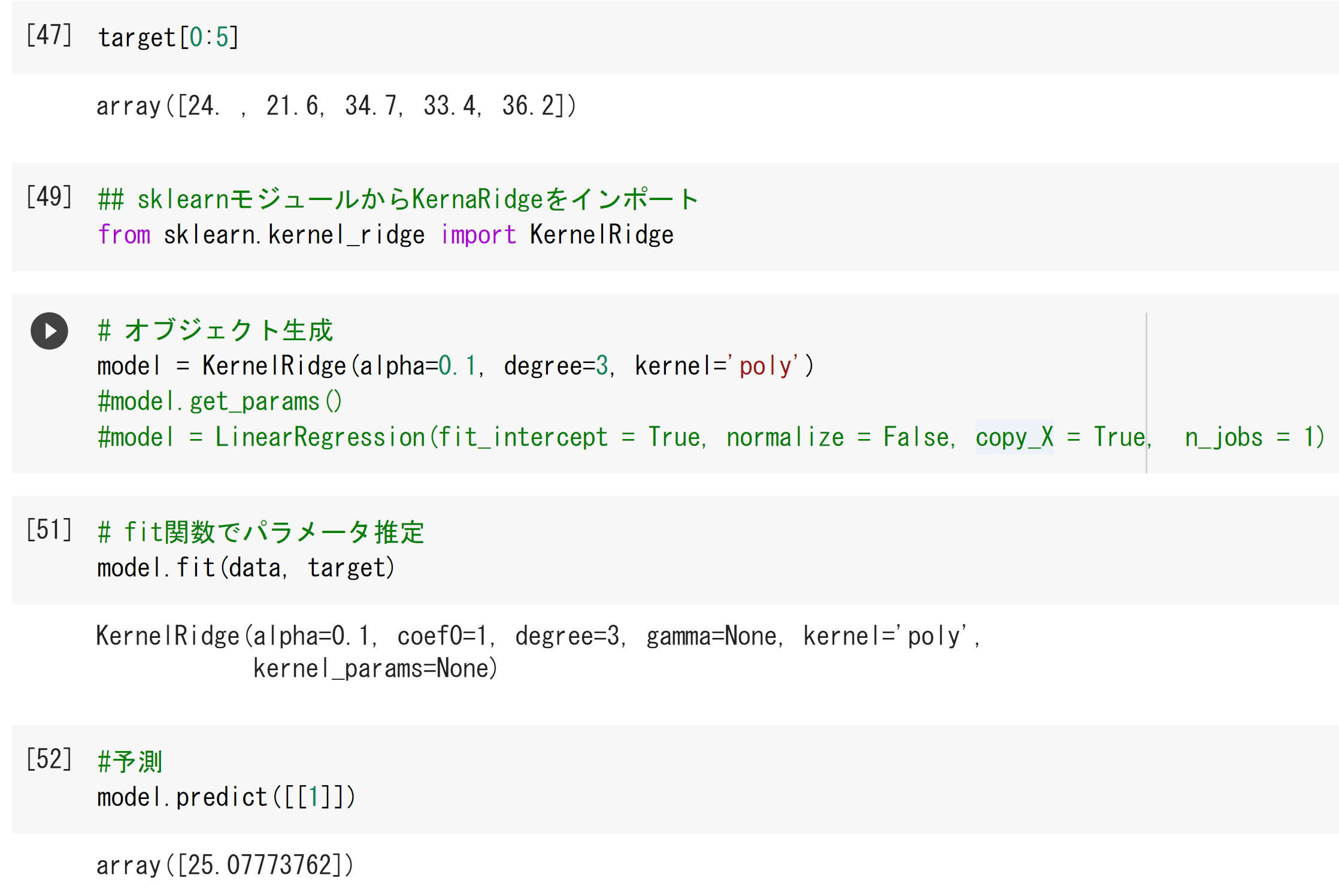
線形回帰のコードに対し、[49][50」を改変しても実施できることを確認
・確認テストなど考察結果
該当なし
・関連記事レポートによる加点
【講義外の私の知識との紐づけ】
人間の感覚器の特性はウェーバーフェフィナー則に従い、
物理量の対数で表示されることが多い(例:音階、音圧レベル、輝度など)
これらも、非線形回帰の一種と言えるかもしれないと感じた
また、同様によく用いられる感覚器モデルとしてフーリエ変換が挙げられる。
異なる位相・周波数の足し合わせで表現するという観点で、
これも非線形回帰の一つと言えるかもしれないと感じた。
第3章:ロジスティック回帰モデル
・1点100文字以上で要点まとめ
ロジスティック回帰は、教師あり学習の分類。
回帰ではない点に注意。
線形回帰と同様に、入力値に重みづけを畳み込み切片を足した、
線形結合を行い、結果をシグモイド関数に入力する。
シグモイド関数は出力が0~1となる関数なので、
出力は、y=1となる確率となる。
シグモイド関数と類似した関数はほかにもある(累積正規分布など)が、
シグモイド関数は、その微分値を自身を用いて表せられるため、
学習時の計算コストを下げられる強みがある。
最適なパラメータを推測ためには、
MSEではなく尤度関数を用いる。
尤度関数はパラメータの関数として表され、
最大尤度となるパラメータが最適なパラメータと推測される。
ただし、計算の単純化のため、
尤度関数の対数の最大値を探索する。
勾配降下法で計算されるが、メモリを大量に要する。
そこで、確率的勾配降下法がよく用いられる。
モデルの正当性評価の指標としては、
正解率のほか、
再現率・適合率とその両方を組み合わせたF値が用いられる。
・実装演習結果
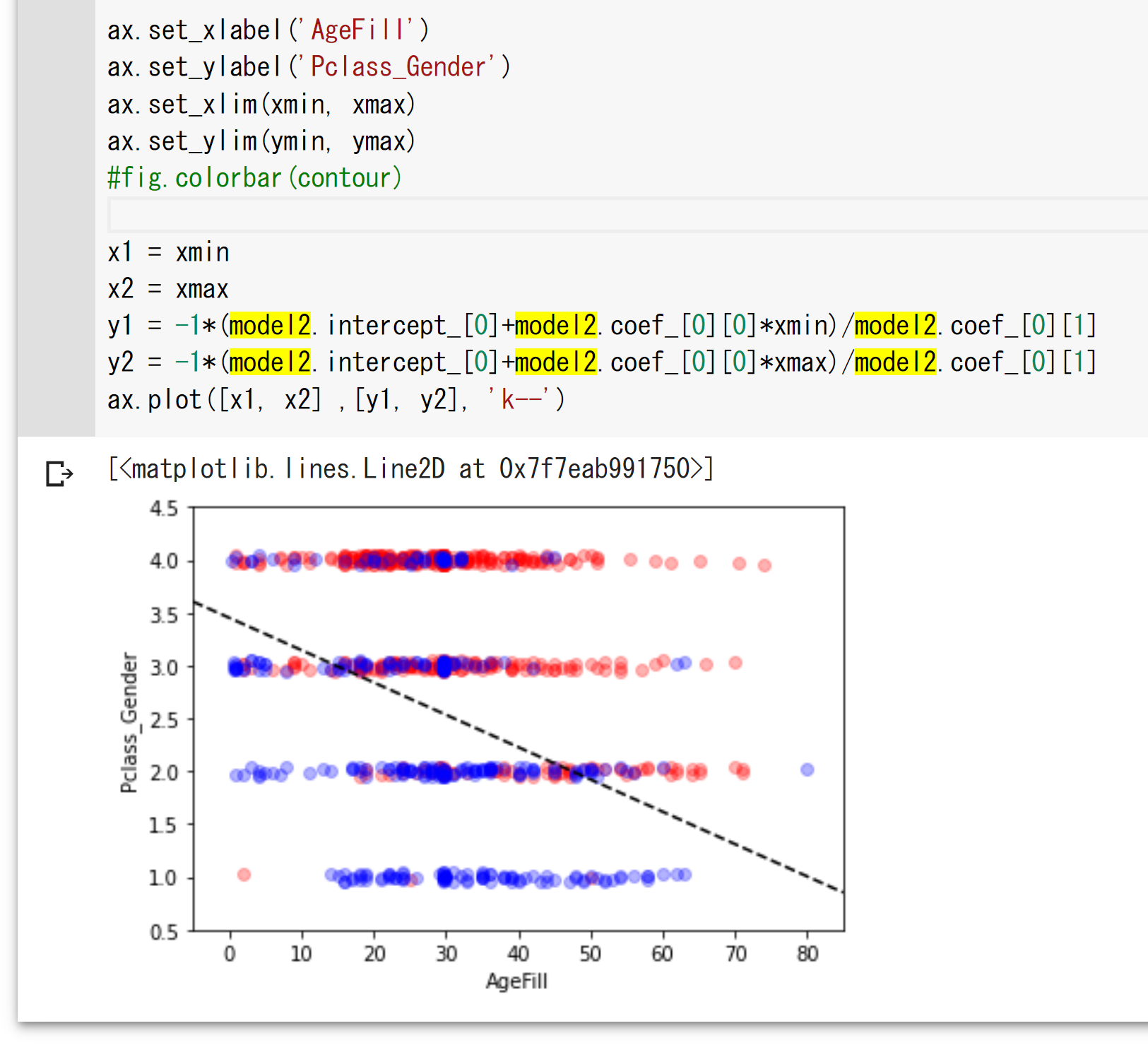
点は、元データの値を示すが、
点線は、サイキットラーンを用いたロジスティック回帰で得られた
傾きと切片から導いた直線を表す
・確認テストなど考察結果
該当なし
・関連記事レポートによる加点
【事業に活用することを想像した】
ロジスティック回帰は出力は0か1となる。
しかし、その前の確率を利用したほうが良い場面もあると思われる。
例えば、自動販売機に飲料水を補充するタスクを考える。
売り切れになっているかを予測するモデルができたとして、
出力の0か1かだけで補充の行動決定をすると、
移動時間のロスは考慮されない。
例えば、1と予測された自動販売機のすぐ近くに、
確率が0.49なので0と出力された自動販売機があれば、
感覚的にそこにも補充すべきと思われる。
なので、最後の0か1かを出力する前段の確率を用いて、
最適探索と組み合わせることもできるのではないかと思う。
第4章:主成分分析
・1点100文字以上で要点まとめ
情報をなるべく残したまま、次元削減する手法。
情報量を分散の大きさと捉える。
ラグランジュ関数の最大値を求めることで、
係数ベクトルを求められるが、
数学的には、係数ベクトルが固有ベクトル、分散が固有値にあたる。
大きい順に分散を、第一主成分から数えていく。
1つの固有値の、固有値の総量に対する割合を寄与率という。
・実装演習結果
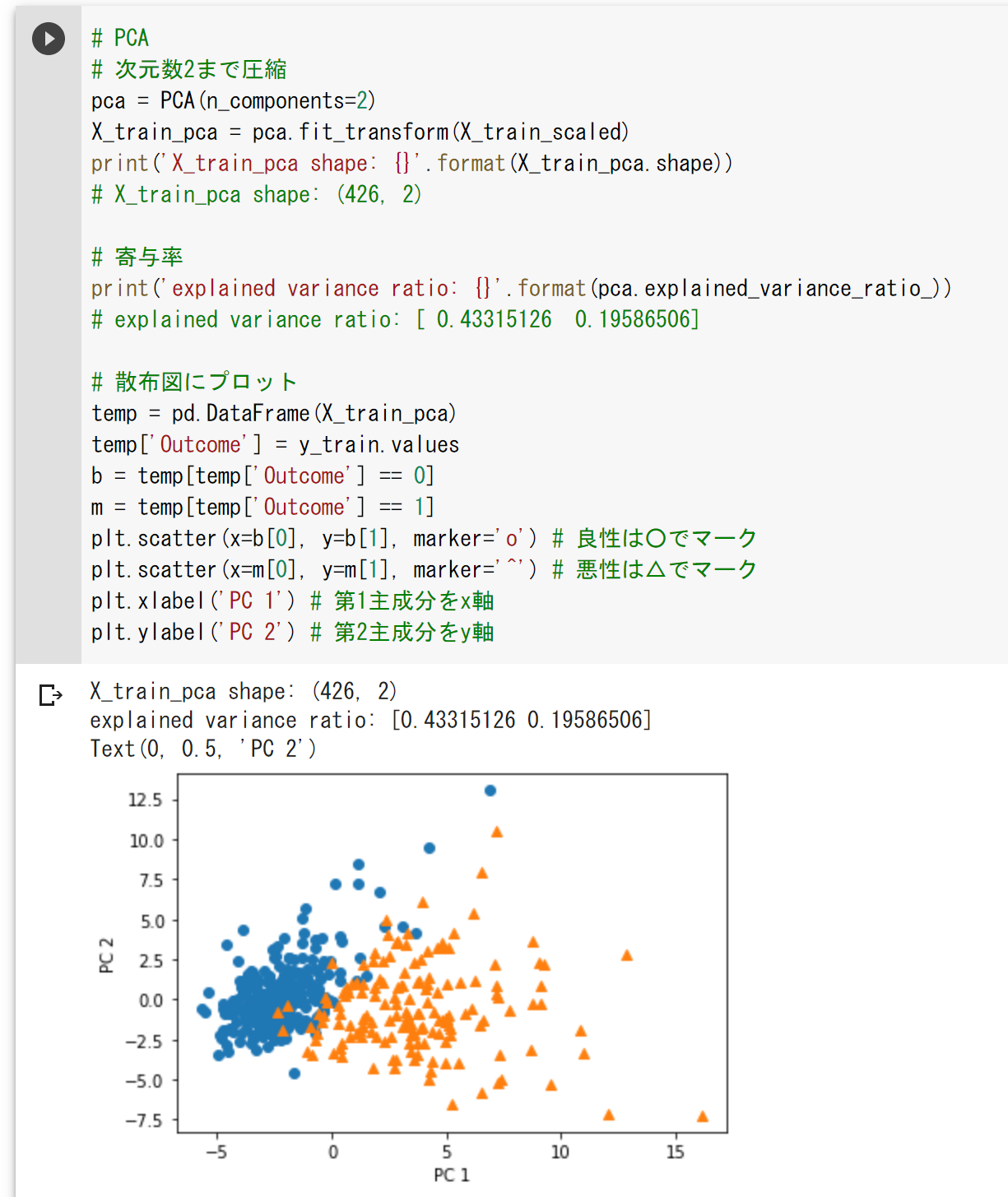
次元数を2次元まで圧縮。
寄与率はそれぞれ第1,2主成分に対し、0.43と0.20。
・確認テストなど考察結果
該当なし
・関連記事レポートによる加点
ステージテスト(148-1~4)から得た気づき
分散が寄与率に大きく影響することから、
入力の外れ値の除去や標準化が、
正確な主成分分析には重要であると感じた。
第5章:アルゴリズム
・1点100文字以上で要点まとめ
・k-近傍法
教師なし分類タスクの一つ。
ある点から、最も近いk個のデータを広い、
多数決でその点のクラス割り当てを行う。
kの数字によって、結果が異なり、
一般的にkが多いほど、クラス間の境界は滑らかになる。
・k-平均法
教師なし分類タスクの一つ。
k個の中心点を定義し、
各データ点について、最も近い中心を求めて、その中心点のクラスに分類する。
クラス毎の中心点を更新したのち、蒸気を繰り返す。
初期の中心によって結果が異なる。
・実装演習結果
・確認テストなど考察結果
該当なし
・関連記事レポートによる加点
該当なし
第6章:サポートベクターマシン
・1点100文字以上で要点まとめ
サポートベクターマシンは、教師なし学習の分類手法。
マージン最大化がコンセプト。
マージンは、決定境界からの距離を表す。
本来は線形分離の手法だが、
入力値にカーネル関数を用いて高次元空間に投影することで、
非線形分離も行えるようになる。
しかし、分離可能なカーネル関数は無限に存在し、
入出力の両方にカーネル関数の内積をとることは計算量が膨大になるため、
この問題を解決するために、カーネルトリックが用いられる。
・実装演習結果
該当なし
・確認テストなど考察結果
該当なし
・関連記事レポートによる加点
該当なし