Fortran 多次元配列のアクセス順序による計算時間の違い

いつものようにNAGFortranのページでFortran Tipsを読み返していたらこんなページを見つけたので、実際に確かめてみました。三次元配列同士の積を、配列の大きさを50-1000まで変えて計算しました。

190801 コードを一部修正しました。

コード

cal_array.f90

program main
  implicit none
  integer :: i,j,k,n
  real(kind=8),allocatable ::  a(:,:,:) , b(:,:,:)
  real(kind=8) :: t1,t2,s1,s2

  do  n = 50,1000,25
    allocate(a(n,n,n))
    allocate(b(n,n,n))
    call random_number(a)
    call random_number(b)
!----------- right -----------!
    call cpu_time(t1)
    do i = 1,n
       do j = 1,n
          do k = 1,n
             a(i,j,k) = a(i,j,k) * b(i,j,k)
          end do
       end do
    end do
    call cpu_time(t2)
 !----------- right -----------!
 !----------- left-----------!
    call cpu_time(s1)
    do i = 1,n
       do j = 1,n
          do k = 1,n
             a(k,j,i) = a(k,j,i) * b(k,j,i)
          end do
       end do
    end do
    call cpu_time(s2)
 !----------- left -----------!
  print*, n, t2-t1, s2-s1
  deallocate(a)
  deallocate(b)
  end do
end     program main

結果

ノイズを減らすために、実際には5回計算を行い算術平均を取っています。

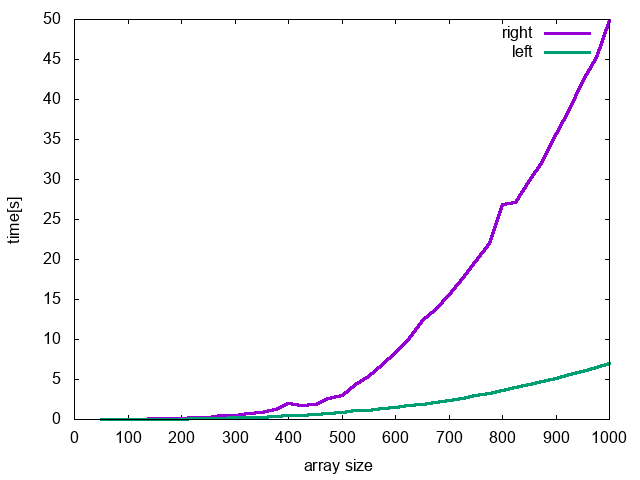
配列の大きさが500を超えたあたりから右側からアクセスした場合の計算時間が大幅に増加しています。一方で左側からアクセスした場合は緩やかにしか変化していません。
小さい配列しか扱わなければそこまで気にしなくても良いのかもしれませんが、大規模な計算をする場合、配列のアクセス順序によって計算時間のパフォーマンスが目に見えて変わりうるという結果になりました。

余談

N=1000の計算だとメモリが16GB前後必要でした。実行される際はお気をつけて…。