経済・ファイナンスデータの計量時系列分析（沖本）７章 Rコード

#７章
７章のRコードの解答例です。
多変量GARCHのライブラリがまだ何個か見つけれてないので、見つけ次第修正。

コードで気になった点
・resultがS4クラスという形で帰ってきたので、それの参照法でちょっと詰まった。（あまり普及していないパッケージだと、結果のオブジェクトの形が一般的でない可能性があるので、そこらへんでエラーが出ていたらちゃんとデータの形を確認して参照の仕方を調べる。）
・時系列系は回帰した後常に誤差項をplot + 誤差項のACF(コレログラム）をプロットして確認してあげるのが良さそう。
・GARCHらへんは色々ライブラリがあるしやりたいことがときによって大きく異なりそうなので、都度調べる必要がありそう。ただ予測の時に機械学習系は分散を考慮しないきらいがあるので、ここは伝統的な計量時系列分析が強みを持てる部分かなとも思う。

##コード　7.4

setwd("Okimoto/7")
library(tidyverse)
library(gdata)
library(lubridate)
library("rugarch")

data = read.xls("msci_day.xls")

data$Date = ymd(data$Date)
data = mutate(data,us_2 = us*us )

par(mfrow = c(2,2))
plot(data$Date,data$us)
plot(data$Date,data$us_2)
acf(data$us,plot = T)
acf(data$us_2,plot = T)


garch11 = ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1,1)),mean.model = list(armaOrder=c(1,0),include.mean = TRUE),distribution.model = "std")
garch11result = ugarchfit(spec = garch11,data = data$us)
garch11result

res_garch = garch11result@fit$residuals
acf(res_garch,plot = T)

gjr11 = ugarchspec(variance.model = list(model = "gjrGARCH", garchOrder = c(1,1)),mean.model = list(armaOrder=c(1,0),include.mean = TRUE),distribution.model = "std")
gjr11result = ugarchfit(spec = gjr11,data = data$us)
gjr11result

res_gjr = gjr11result@fit$residuals
acf(res_gjr,plot = T)

egarch11 = ugarchspec(variance.model = list(model = "eGARCH", garchOrder = c(1,1)),mean.model = list(armaOrder=c(1,0),include.mean = TRUE),distribution.model = "std")
egarch11result = ugarchfit(spec = gjr11,data = data$us)
egarch11result

res_egarch = egarch11result@fit$residuals
acf(res_egarch,plot = T)

#結果
##output
長いので一部抜粋

---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics 	
-----------------------------------
GARCH Model	: gjrGARCH(1,1)
Mean Model	: ARFIMA(1,0,0)
Distribution	: std 

Optimal Parameters
------------------------------------
         Estimate  Std. Error    t value Pr(>|t|)
mu     824.583821   10.007052 8.2400e+01 0.000000
ar1      1.000000    0.000334 2.9979e+03 0.000000
omega    1.274867    0.573333 2.2236e+00 0.026175
alpha1   0.000000    0.009791 7.0000e-06 0.999995
beta1    0.940971    0.013911 6.7643e+01 0.000000
gamma1   0.090982    0.022393 4.0631e+00 0.000048
shape    9.101599    2.035765 4.4708e+00 0.000008

Robust Standard Errors:
         Estimate  Std. Error    t value Pr(>|t|)
mu     824.583821    1.413686 5.8329e+02 0.000000
ar1      1.000000    0.000401 2.4957e+03 0.000000
omega    1.274867    0.638501 1.9967e+00 0.045863
alpha1   0.000000    0.010419 6.0000e-06 0.999995
beta1    0.940971    0.019285 4.8793e+01 0.000000
gamma1   0.090982    0.026539 3.4282e+00 0.000608
shape    9.101599    2.640493 3.4469e+00 0.000567

LogLikelihood : -4999.902 

Information Criteria
------------------------------------
                   
Akaike       7.1990
Bayes        7.2254
Shibata      7.1989
Hannan-Quinn 7.2089

Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
                        statistic   p-value
Lag[1]                      5.973 1.453e-02
Lag[2*(p+q)+(p+q)-1][2]     6.355 1.652e-05
Lag[4*(p+q)+(p+q)-1][5]     7.315 1.448e-02
d.o.f=1
H0 : No serial correlation

Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
                        statistic p-value
Lag[1]                      4.263 0.03896
Lag[2*(p+q)+(p+q)-1][5]     5.527 0.11599
Lag[4*(p+q)+(p+q)-1][9]     6.195 0.27639
d.o.f=2

Weighted ARCH LM Tests
------------------------------------
            Statistic Shape Scale P-Value
ARCH Lag[3]    0.6934 0.500 2.000  0.4050
ARCH Lag[5]    0.7232 1.440 1.667  0.8164
ARCH Lag[7]    1.0355 2.315 1.543  0.9077

Nyblom stability test
------------------------------------
Joint Statistic:  2.3528
Individual Statistics:              
mu     0.08768
ar1    0.45109
omega  0.08341
alpha1 0.23005
beta1  0.11746
gamma1 0.13395
shape  0.58373

Asymptotic Critical Values (10% 5% 1%)
Joint Statistic:     	 1.69 1.9 2.35
Individual Statistic:	 0.35 0.47 0.75

Sign Bias Test
------------------------------------
                   t-value    prob sig
Sign Bias            1.871 0.06159   *
Negative Sign Bias   2.237 0.02547  **
Positive Sign Bias   1.049 0.29439    
Joint Effect         9.530 0.02302  **


Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
  group statistic p-value(g-1)
1    20     58.04    7.858e-06
2    30     88.40    6.398e-08
3    40    126.96    3.041e-11
4    50    153.18    1.178e-12


Elapsed time : 0.662637 

##graph

自己相関がかなり強いのはdailyを使ってるから？
（Monthlyにして再チェック必要）

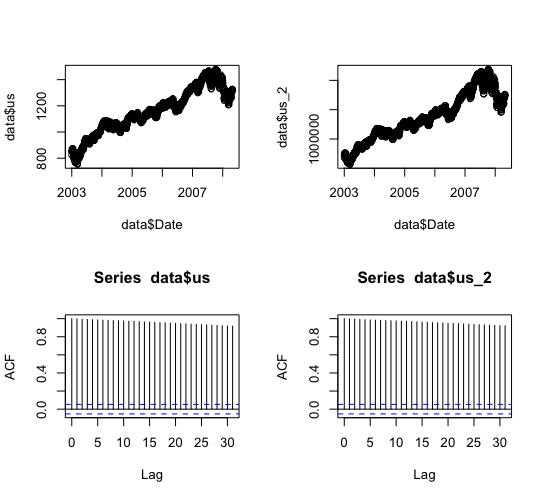
residualの系列相関はちゃんと落とせているので、推定はうまくいっていそう
（homoscedasticityのモデルと比較する必要あり）

##参考にした記事
GARCH系のライブラリまとめ
https://www.rdocumentation.org/packages/rugarch/versions/1.4-4/topics/ugarchspec-methods
S4クラスのオブジェクトの扱い方（resultがS4クラスで帰ってきてちょっと参照の仕方に困ったので）
http://www.okadajp.org/RWiki/?S4+%E3%82%AF%E3%83%A9%E3%82%B9%E3%81%A8%E3%83%A1%E3%82%BD%E3%83%83%E3%83%89%E5%85%A5%E9%96%80#h39bd201
GARCH周りの基本的なライブラリのまとめ
http://user.keio.ac.jp/~nagakura/R/ts_R4.pdf