正しいモデル選択をするためにモデル評価が大事になってきます。いくつか方法がありますが、代表的なものを列挙します。
- Hold Out法
- Cross Validation法
- Leave One Out法
- Bootstrap法
- WAIC
- WBIC
leave one outはcross validationにおいて、データ数とグループ数が等しい場合を指します。まずはこの方法を使って、性能評価を行い、正しくモデル選択ができるか検証してみます。
テストデータの作成
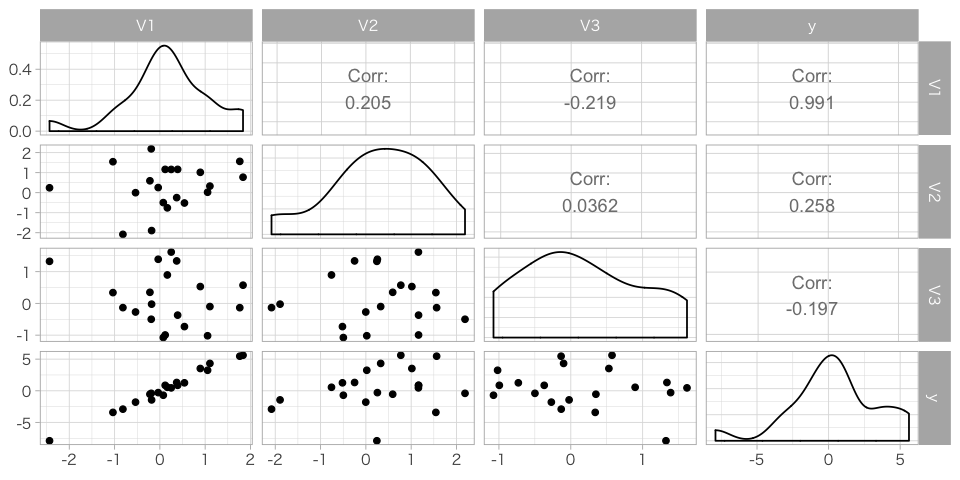
下の因果グラフに基づき、テストデータを生成します。誤差項はすべて、正規分布に従うとします。1回のサンプリング数は10とします。
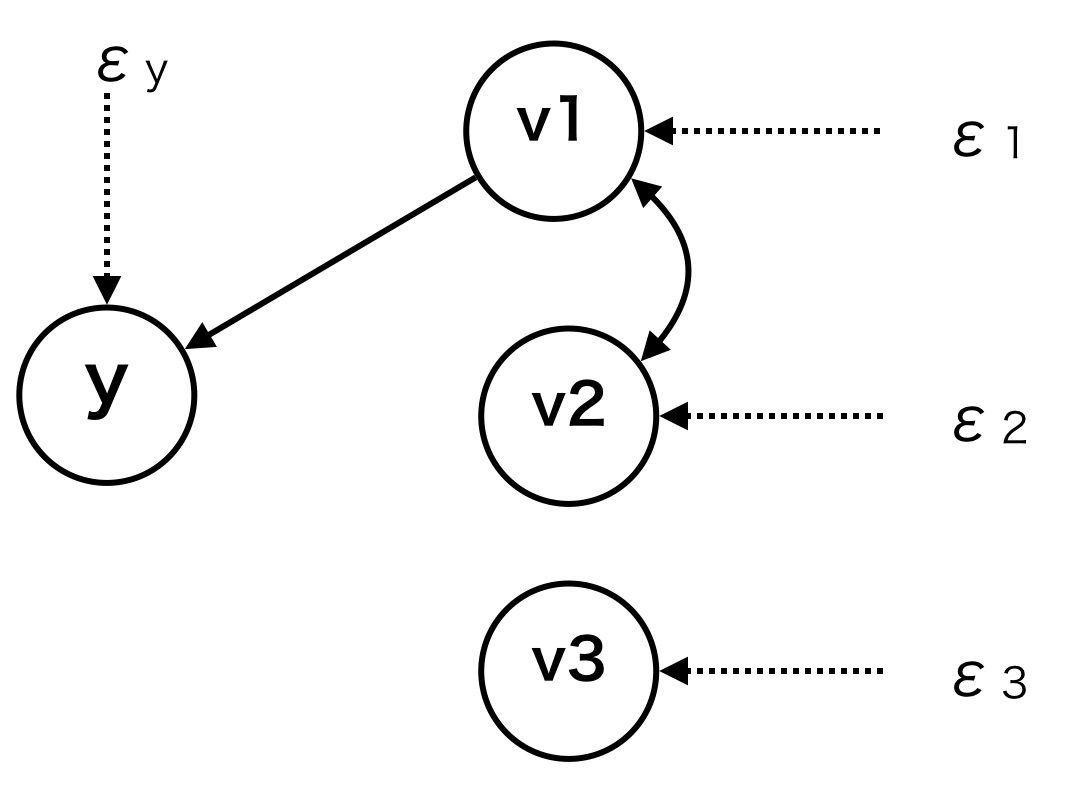
n= 10
mu = c(0,0)
sd = c(1,1)
cor =.2
cov = sd %*% t(sd) * cor
diag(cov) = sd^2
generate_data = function(){
mvrnorm(n,mu,cov) %>% as.tibble() %>% mutate(V3 = rnorm(n,0,1),y=3 * V1 + rnorm(n,0,.5))
}
モデルの候補
- Y ~ V1 (正しいモデル)
- Y ~ V1+V2
- Y ~ V1+V2+V3
- Y ~ (V1+V2)^2 (相互作用も考慮したモデル)
- Y ~ (V1+V2+V3)^2
Leave one out法
では、Leave one outに基づいてモデルを選択してみます。
models = list(y~V1, y~V1+V2, y~V1+V2+V3)
result = models %>% map(~{
model = .x
1:nrow(df) %>% map(
~(lm(model, data=df[-.x,]) %>% predict(df[.x,]) - df$y[.x])^2
)
})
result %>% simplify_all() %>% set_names(str_c("model_",1:3)) %>% as.tibble %>% summarise_all(mean) %>% which.min
# >>model_1
上記のデータセットでは正しくモデル1が選ばれたようです。
次に上記の流れ(データ生成+モデル選択)を1000回繰り返します。果たして正しいモデルを選択できたのでしょうか?
models = list(y~V1, y~V1+V2, y~V1+V2+V3, y~(V1+V2)^2, y~(V1+V2+V3)^2)
1:100 %>% map(~{
df = generate_data()
result = models %>% map(~{
model = .x
1:nrow(df) %>% map(
~(lm(model, data=df[-.x,]) %>% predict(df[.x,]) - df$y[.x])^2
)
})
result %>% simplify_all() %>% set_names(1:length(models)) %>% as.tibble %>% summarise_all(mean) %>% which.min
})
result %>% unlist %>% as_tibble %>%
ggplot(aes(value)) + geom_bar() + labs(x="モデル",y="カウント数")
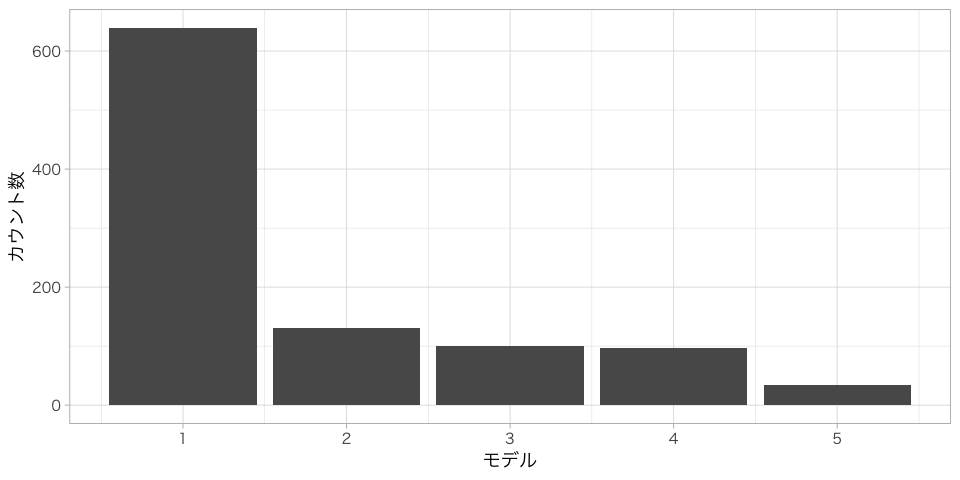
さて、気になる結果です。一番選択されやすいモデルは正しいモデル①であったものの、それ以外のモデルも少なからず選択されています。
| Model | Count |
|---|---|
| 1 | 639 |
| 2 | 130 |
| 3 | 101 |
| 4 | 96 |
| 5 | 34 |
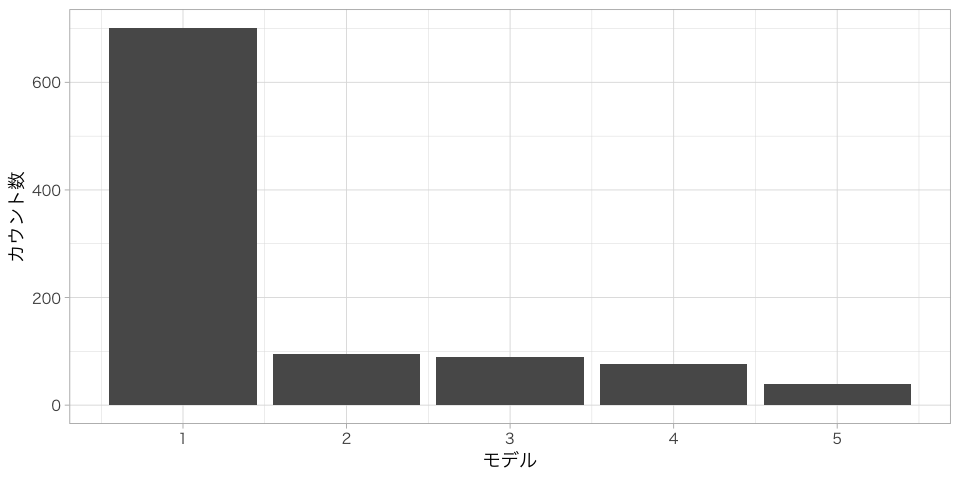
次にサンプルサイズを100に増やして、同じように実験してみます。
結果はこちら。
| Model | Count |
|---|---|
| 1 | 701 |
| 2 | 95 |
| 3 | 89 |
| 4 | 76 |
| 5 | 39 |
想像どおり、サンプル数を増やすことによって、より正しくモデル選択ができるようになりました。
しかし、それでも正答率は70%ほど。データのみから正しいモデルを選択することはかなり困難な印象です。Leave one out以外にWAICも汎化誤差の近似として使いますが、性能は似たようなものらしいです(うろ覚え)。
今回は正規分布かつ線形モデルでテストデータを作成しました。
しかし、現実は背景因子の確率分布も複雑であり、因果関係も線形構造ではないことが多いでしょう。
やはり、その道の専門家と手を取り合い、少しでも多くのドメイン知識に基づいて、モデルを作成していく&候補を絞っていく作業が重要になってくるのではないでしょうか。
Bootstrap法(追記)
1つの標本からリサンプリングを繰り返して生成する標本をブートストラップ標本と呼びます。
手元のデータから最尤推定で求めたパラメタでMSEを計算しても、真のデータ分布を使ったMSEはそれより大きくなる。それをブートストラップ標本を使って修正する方法です。詳しくは「はじパタ第2章」参照してください。
result = 1:100 %>% map(~{
df = generate_data()
models %>% map(~{
model=.x
expected_bias = 1:100 %>% map_dbl(~{
sample = df %>% sample_frac(replace=T)
fit = lm(model,data=sample)
fitted_MSE = fit$residuals^2 %>% mean
predicted_MSE = (predict(fit, df) - df$y)^2 %>% mean
bias = predicted_MSE-fitted_MSE
bias
}) %>% mean
lm(model,df)$residuals %>% .^2 %>% mean + expected_bias
}) %>% which.min
})
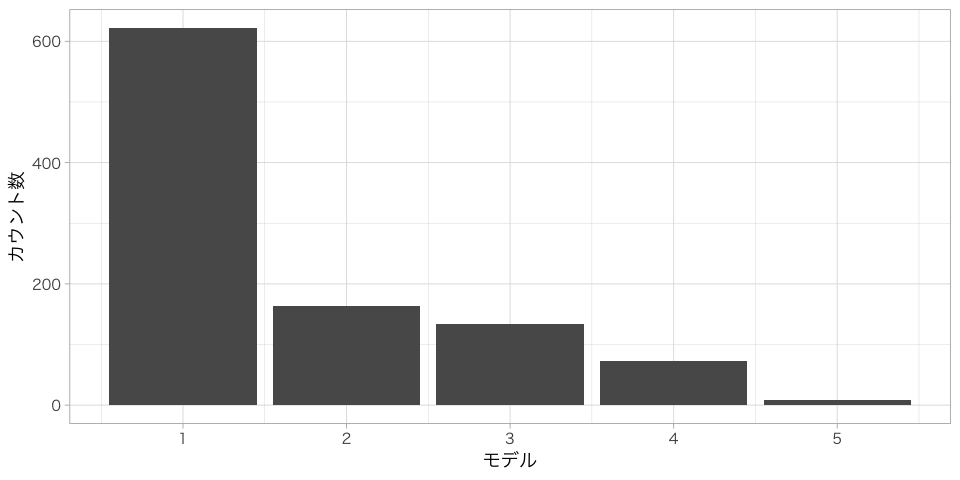
気になる結果は。。。
| Model | Count |
|---|---|
| 1 | 622 |
| 2 | 164 |
| 3 | 134 |
| 4 | 72 |
| 5 | 8 |
今回のテストデータだけからは結論付けれませんが、LOOVと比較すると性能が悪いような気がします。