はじめに
この記事は、統計学を勉強し始めた人に向けて書いています。最尤法やベイズという用語は聞いたけれども、具体的にイメージがしにくいという人に向けて、それらの手法の一面を解説する内容です。
最尤法やベイズといった手法の根幹はとてもシンプルです。そして多くの教科書では最初にその数式を見せ、考え方の基礎を解説します。しかし統計の初学者にとって、それらシンプルな式が意味することを見出すのはとても難しいです。そこでこの記事では、統計学を勉強し始めた頃の自分を思い出しながら、まず前回説明した最尤法の限界を説明し、それとの対比としてリッジ回帰を紹介し、更にリッジ回帰をベイズ的に捉え直すことでベイズ統計学の考え方を説明したいと思います。
なおこの記事内での数式や記号は、基本的に機械学習の教科書「パターン認識と機械学習」(C. M. Bishop)を踏襲しています。また、この記事は前回「最尤法とは、ベイズとは (1.最小二乗法と最尤法)」の続きとなっております。
前回URL → https://qiita.com/YusukeToda1984/items/1b0a10ec1f847c6cbd36
最尤法の弱点
前回の記事では、まず最小二乗法について説明し、それに対して確率の考え方を導入することで最尤法についての説明を行いました。最尤法はパラメータの推定手法として「良い」手法であることは、数学的にも証明されています。非常にかいつまんで言うと、データの数が十分に大きいケースでは、パラメータの推定値が真の値に近づくという性質などが示されています。しかし、時に十分な数のデータを得られないことも多い現実の問題で、最尤法はうまく機能するのでしょうか?
ここで、シミュレーションデータを用いた具体例をお見せしましょう。あなたは教員で、12人の生徒を受け持っており、10教科(数学、物理、化学、生物、現代文、古文、世界史、日本史、音楽、体育)の生徒の期末成績のデータを持っています。生徒たちはとある模試を受け、その点数が公表されました。その模試は秘匿性の高いもので、あなたは問題の内容について知ることができません。そこであなたは、期末試験の点数と模試の点数を比較することで、模試の内容がどのようなものであったか推論することにしました。
この問題では、学校の成績が独立変数 $x_{ij}$ 、模試の点数が従属変数 $t_{j}$ となります。ここでは $i = 1, ..., 10$ が科目、$j = 1, ..., 12$ が生徒に対応します。$x_{ij}$ と $t_j$ をプロットした結果が Fig. 1 です。

このデータはシミュレーションで作成しているので、$x$ と $t$ の真の関係性を知ることができます。この式は Fig. 1 にも点線で表示してあります。実はこの模試では、数学・物理・化学の問題しか出題されていませんでした。以下の式は、データの生成に使用した真の関係性です。実際にはこれは分からないので、データからこの式を推定したいと思います。
\begin{align}
t &= 50 + 1.3 x_1 + 0.5 x_2 + x_3 + e \tag{1} \\
p(e) &= N(e|0, 9) \tag{2}
\end{align}
推定のため、あなたは次のようなモデルを立てました。各教科の点数にパラメータ $w_i$ を掛けて足し合わせることで模試の点数を表現できるというモデルです。これは適切なモデルと言えます。もし物理・古文・日本史の問題が $1:2:1$ の割合で出たら、対応する $w_i$ の値を同じ比率に設定すれば、模試の点数を表現できるだからです。
\begin{align}
t = w_0 + \sum_{i = 1}^{10} w_i x_i + e \tag{3} \\
p(e) = N(e|0, \sigma_e^2) \tag{4}
\end{align}
ここまでで出てきた文字を整理します。なお、これらは真の式 $(1), (2)$ とは関係ありません(本当は真の式は知らないはずなので)。
- $x_i$ は独立変数で、教科 $i$ の点数です。
- $t$ は従属変数で、模試の点数です。
- $w_i$ はパラメータで、教科 $i$ がどれほど模試の点数に影響しているかを表します。
- $e$ は残差で、このモデルで説明できない効果です。出題傾向と得意分野の組合せや、当日の生徒の体調などが考えられます。ここでは分散が $\sigma_e^2$ の正規分布に従っていると仮定します。
モデルが立てられたので、さっそく最尤法で推定してみましょう。こちらが推定されたパラメータの値です。Fig. 2には赤い線で図示しています。
\begin{align}
(w_0, ..., w_{10}, \sigma_e^2) =
\ (&-103.20, \ 1.98, \ -0.88, \ 2.32, \ 0.13, \ 1.18, \\
&0.51, \ -0.79, \ -0.44, \ -0.73, \ 1.66, 1.34)
\end{align}

Fig.2 によると、4番目の生物以外の科目は模試の成績に影響しているように見えます。しかし、この結果にはいくつか疑問が挙がります。いくつかの教科については、期末試験の点数が悪いほど模試の成績は良いという結果になっています。また、模試で試験されたとは思えない音楽や体育も模試に影響しているとされてしまいました。これはどういうことでしょうか?
過学習とリッジ回帰
原因は、パラメータの数に対してデータの数が少なすぎる点にあります。今回の場合、パラメータ $w_i$ の数は $11$ ありますが、生徒の人数は $12$ です。このような場合、最尤法でパラメータを正確に推定するのは困難です。最尤法は、モデルからデータが生成される確率である尤度を最大化する方法です。今回のようにデータが少ないと、モデルがデータに当てはまるように無理やりパラメータを調整してしまいます。この現象は過学習、オーバーフィッティングと呼ばれます。
データの件数が足りない時に過学習を回避するにはどうすればよいでしょうか。そのために一度、最尤法の枠組みを置いておき、代わりに前回登場した最小二乗法を思い出してみます。なお、この例では残差 $e$ が正規分布に従っていると仮定したので、最小二乗法と最尤法の結果は一致します。
最小二乗法の考え方を元に、モデルを表し直してみます。
- 従属変数 $t_j$ は、推定値 $y_j$ と残差 $e_j$ に分解できる。なお、$j=1,...,12$ はそれぞれの生徒を表す。
t_j = y_j + e_j \tag{5}
- 推定値 $y$ は、独立変数 $x_1, ..., x_{10}$ の多項式になっている。
y_j = w_0 + \sum_{i = 1}^{10} w_i x_{ij} \tag{6}
- パラメータは、残差の二乗和を最小化するものとして得られる。
\sum_{j=1}^{12} e_j^2 \tag{7}
さて、このまま最小二乗法を当てはめると最尤法と同じように失敗してしまします。そのため、これに別の仮定を加えなければならなさそうです。
最小二乗法(最尤法)で推定されたモデルのパラメータの値は、真の値よりも大きかったり小さかったりと、かなりぶれた値になっていました。例えば、本来は $0$ であるはずの $w_4, ..., w_{10}$ が、かなりぶれた値になっています。このことに注目すると、残差と同時にパラメータの値も小さくすればよい、と考えることができそうです。
この発想を具体的にするために、残差二乗和の代わりに最小化するものを考えましょう。以下が今回導入する新しい指標です。
\sum_{j=1}^{12} e_j^2 + \lambda \sum_{i=0}^{10} w_i^2 \tag{8}
第一項は残差二乗和で、第二項はパラメータの二乗和です。ただ、残差とパラメータを同程度に小さく抑えるのが良いとは限りません。第二項にかかる $\lambda$ は「どちらの項をより小さく抑えるか」の調整のために加えられた新しいパラメータです。
この指標の最小化によってパラメータを推定する手法はリッジ回帰と呼ばれ、統計解析において有名な手法の一つです。成績のサンプルデータに当てはめた結果を見てみましょう。Fig. 3 の青線が結果を示しています。なお、$\lambda$ の値は通常、他のパラメータ $w_i$ とは別に交差検証などの方法を使って決定しますが、ここでは説明は省きます。
\begin{align}
(w_0, ..., w_{10}, \lambda) = (& 118.91, \ 1.03, \ 0.38, \ 0.58, \ -0.03, \ 0.02 ,\\
&0.05, \ 0.01, \ 0.02, \ 0.19, \ -0.36, \ 0.88)
\end{align}
 パラメータ $w_i$ の推定値がいずれも真の値に近づいていることが分かります。このように「パラメータの値を小さくする」という仮定を入れることで、データ件数が少ない場合も推定が安定することが分かります。
パラメータ $w_i$ の推定値がいずれも真の値に近づいていることが分かります。このように「パラメータの値を小さくする」という仮定を入れることで、データ件数が少ない場合も推定が安定することが分かります。
ベイズ的リッジ回帰
前の記事では最初に最小二乗法を説明し、それに確率分布を導入することで最尤法の説明をしました。今回も、先ほど説明したリッジ回帰に確率分布を導入することで、ベイズの考え方を取り入れていきます。
まずは最尤法の設定を確認しましょう。式 $(9)$ は独立変数 $x_i$ と従属変数 $t$ の関係を表し、式 $(10)$ は残差が正規分布に従うという設定を表しています。
\begin{align}
t = w_0 + \sum_{i = 1}^{10} w_i x_i + e \tag{9} \\
p(e) = N(e|0, \sigma_e^2) \tag{10}
\end{align}
ここまでだと通常の最尤法ですので、もう一つ仮定を加えます。残差だけではなく、パラメータにも確率分布を導入します。
p(w_i) = N(w_i|0, \sigma_w^2) \ \ \ \ (j = 1, ..., 10) \tag{11}
パラメータ $w_i$ が $0$ を中心とした正規分布に従うと仮定しています。これはリッジ回帰において、残差二乗和に加えてパラメータ二乗和についても最小化を行ったことに対応しています。最尤法で発生する過学習を防ぐため、「パラメータは0付近に分布する」という仮定を入れることで、徒にパラメータの推定値が振れてしまうことを防ぎたいのです。
さて、パラメータの確率分布の設定ができたところで、その推定を行ってみましょう。しかしこの場合、何を最大化/最小化すればよいのでしょうか。
最尤法では $p(\mathbf{t}|\mathbf{X}, \boldsymbol{\theta})$ で表される尤度を最大化することで、パラメータの推定を行いました。なお、記号はそれぞれ従属変数 $\mathbf{t}$、独立変数 $\mathbf{X}$、パラメータ $\boldsymbol{\theta}$ を表します。しかし、この場合は尤度の最大化で問題を解決することはできません。尤度を計算すると
\begin{align}
p(\mathbf{t}|\mathbf{X}, \boldsymbol{\theta})
& = p(\mathbf{t}|\mathbf{X}, w_0, ..., w_{10}, \sigma_e^2, , \sigma_w^2) \\
& = p(e) \\
& = N(e|0, \sigma_e^2) \tag{12}
\end{align}
となり、残差の分布しか考慮されません。なぜなら尤度において、パラメータ $\boldsymbol{\theta}=(w_0,...,w_{10})$ はあくまで条件づける側の変数として組み込まれているからです。$w_i$ が条件づける変数である以上、$w_i$ の値は既に与えられているものと見なされます。最尤法ではパラメータ $w_i$ を動かして尤度が最大となる推定値を探しますが、この時 $w_i$ 自身の分布は考慮されません。
では、何を最大化するとよいのでしょうか。パラメータの分布を考慮するなら、パラメータが条件づけられる変数として組み込まれている指標を使う必要があります。ここで、ベイズの定理を思い出してみましょう。
p({\rm B}|{\rm A}) = \frac {p({\rm A}|{\rm B})p({\rm B})} {p({\rm A})} \tag{15}
この式は条件付き確率の定義から導出されるので、どのような場合も成り立ちます。この式の ${\rm A}$ に $\mathbf{t}$, ${\rm B}$ に $\boldsymbol{\theta}$ を代入してみると、尤度を使って「パラメータが条件づけられる方に入っている確率」を作ることができます。なお $\boldsymbol{\rm{X}}$ は確率変数ではないので、必要なところに適宜入ります。
\begin{align}
p(\boldsymbol{\theta}|\boldsymbol{\rm{X}}, \boldsymbol{\rm{t}}) & =
\frac {p(\mathbf{t} |
\boldsymbol{\theta}, \boldsymbol{\rm{X}}) \,
p(\boldsymbol{\theta})}
{p(\mathbf{t})} \\
& \propto p(\mathbf{t}|\boldsymbol{\theta}, \boldsymbol{\rm{X}}) \, p(\boldsymbol{\theta})
\tag{15}
\end{align}
尤度 $p(\mathbf{t}|\boldsymbol{\theta}, \boldsymbol{\rm{X}})$ とパラメータ $p(\boldsymbol{\theta})$ の分布の積を取ることで、$p(\boldsymbol{\theta}|\boldsymbol{\rm{X}}, \mathbf{t})$ という新しい分布を導き出すことができました。最後の式展開で分母を省きましたが、これは $p(\mathbf{t})$ は両辺を積分すると1になることを保証する、いわば積分定数のようなものだからです。さて、この式の意味について、パラメータの分布 $p(\boldsymbol{\theta})$ と比較して考えてみます。
$p(\boldsymbol{\theta})$ はパラメータに対して、データに関係なくあらかじめ設定した分布で、ここでは平均 $0$ の正規分布としました。一方 $p(\boldsymbol{\theta}|\boldsymbol{\rm{X}}, \mathbf{t})$ は、データ $\boldsymbol{\rm{X}}, \mathbf{t}$ で条件づけられており、データが与えられた上でのパラメータの分布であると言えます。
これらは重要な分布なので、命名することにします。$p(\boldsymbol{\theta})$ はデータが得られる前の時点でパラメータに課せられる分布なので 事前分布 と呼びます。一方 $p(\boldsymbol{\theta}|\boldsymbol{\rm{X}}, \mathbf{t})$ はデータが与えられた後、データを元に計算される分布なので 事後分布 と呼びます。
事後分布は、尤度 $p(\mathbf{t}|\boldsymbol{\theta}, \boldsymbol{\rm{X}})$ と事前分布 $p(\boldsymbol{\theta})$ の積で表されます。すなわち、最小二乗法や最尤法で考慮される尤度と、今回式 $(11)$ として導入されたパラメータの事前分布の両方を考慮できる指標と言えます。それでは、最尤法で尤度が最大となる $\boldsymbol{\theta}$ を推定値としたように、事後分布が最大となる $\boldsymbol{\theta}$ を推定値としてプロットしてみましょう。先程のリッジ回帰と同様に、過学習が避けられていることが分かります。
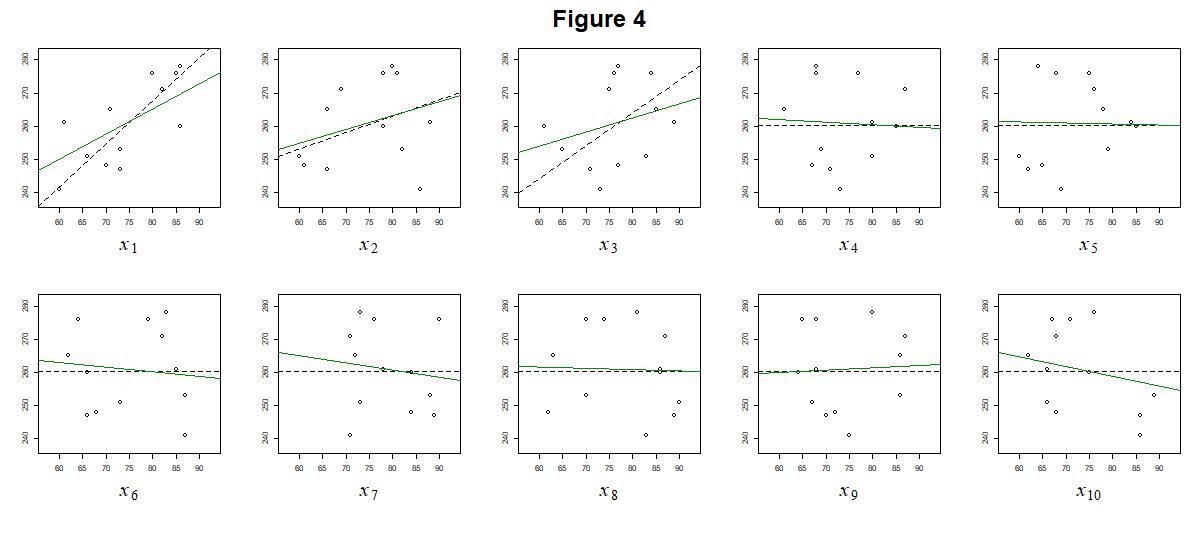
前回の記事では、最小二乗法に確率を用いることで最尤法を導出しました。ここまでの話はそれと全く同じ流れになっており、まず確率に基づかないリッジ回帰を導入して、そのパラメータに対する仮定に確率を導入することでベイズ的な取り扱いについて説明してきました。しかし、ベイズ的な考え方にはもう一つとても重要な特徴があります。最後にそれを説明しましょう。
ベイズ的な考え方
先程のセクションでは「事後分布が最大となる $\boldsymbol{\theta}$」を推定値としました。こうした考え方はMAP推定 (maximum a posteriori, 最大事後確率推定) と呼ばれています。この手法ではベイズの定理を活用していますが、いわゆる「ベイズ統計学」と呼ばれる考え方の一部に過ぎません。
ここまでに登場した最小二乗法、最尤法、MAP推定のいずれにおいても、パラメータには「真の値」があり、それをいかに正確に推定するかという問題を考えてきました。そのために使われるツールは、残差二乗和・尤度・事後分布など様々でしたが、目的としては真のパラメータをより正確に当てることに注目してきました。
しかし、いわゆるベイズ主義においては、パラメータの「真の値」というものを考えることはありません。代わりに、パラメータはあくまで「分布」として捉えられます。データが与えられない状態では、パラメータの分布に関してはあいまいな分布しか仮定できません(事前分布)。データが与えられ尤度が計算できると、事前分布との積を取ることでよりデータに則した分布を得ることができます(事後分布)。
具体的な例を見てみましょう。Fig. 5 は、サンプルデータにおいて得られたパラメータの事前分布(赤)と事後分布(青)を図示しています。黒の縦線は、サンプルデータを生成するために用いられた「真の値」です。

真のパラメータが $0$ でない $w_1, w_2, w_3$ については、事後分布のピークが事前分布のピークよりも真のパラメータの値に寄っていることが分かります。これは「データが得られる前は平均 $0$ の正規分布を想定していたが、データを参照した結果、$0$ より大きい値を中心とした分布の方が現象をうまく説明できた」ことを表します。また他のパラメータに関しても、事後分布の形が $0$ を中心に鋭くなっています。これは「事前に仮定していた平均 $0$ の正規分布にデータが加わったことで、パラメータが $0$ 付近に分布するという確信が強くなった」と言えます。
ベイズ統計学の利点
これまで、簡単な回帰分析を例にとり、ベイズ統計学の基礎的な考え方を説明してきました。これにより、ベイズ統計学のコンセプトについて、ぼんやりとしたイメージをつかめて頂ければ嬉しいです。ただ、ここで説明した例はベイズ統計学の応用例のほんの一部に過ぎず、実際は更に色々な応用方法があります。ここでは最後にベイズ統計学の利点について、ごく簡単に触れます。
まず、事前分布を導入したことにより、パラメータの推定に柔軟な事前の仮定を反映させることができる点が挙げられます。下の図はプログラミング言語RのBGLRというパッケージに使われている、線形回帰のパラメータの事前分布です[1]。正規分布(黒線)を使用する場合はベイズ的リッジ回帰になりますが、それ以外にも自由な形の分布が指定できることが分かります。
また、パラメータを分布として扱うことで、パラメータの推定方法も工夫できるようになります。尤度を扱う最尤法と異なり、ベイズ的な考え方では全ての登場人物を確率分布として捉えることができるからです。具体的には、MCMC(マルコフ連鎖モンテカルロ法)や変分ベイズといった方法が挙げられます。これにより、計算には多くの時間を要するかもしれないものの、複雑なモデルであっても適切なパラメータの推定を行うことができます。
その他、以下のような利点が考えられます。
- データ内の欠測値を変数として扱うことができるので、欠損を含むサンプルを除外しなくて良い(最尤法の場合は除外しなければならないケースが多い)
- 事後分布を推定すれば、パラメータの推定値のぶれを評価することができる(複雑なモデルの場合、最尤法でパラメータのぶれを評価するには工夫が必要にあなる)
逆に、最尤法に比べた欠点として考えられるのは以下の点でしょうか。
- 事後分布を推定しなければいけないので計算に時間がかかる
- 事前分布の設定が適切でないと説得力のある結果ではなくなる
どちらの手法を取るのが良いかは、ケースバイケースということになるでしょう。傾向として、単純な回帰や分類問題においては最尤法を用いた統計学を使うことが主で、複雑なモデルを扱おうとするとベイズがちらほらと顔を出すように思います。
以上、2回分の記事で最尤法とベイズという統計学の枠組みについてお話してきました。読んで下さった方の参考に少しでもなれていれば幸いです。ただし、この記事は分かりやすさを重視したため、結果の導出過程をすっとばしています。本格的に勉強したい方であれば、より詳しい資料を参考にして自分で計算してみることもお勧めします。
参考文献
[1] Pérez, P., & Campos, G. D. (2014). Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics, 198(2), 483-495. doi:10.1534/genetics.114.164442
図の描画はRで行いました。スクリプトをGitHubで公開しています → https://github.com/YT100100/QiitaArticles/blob/master/20200426_WhatIsBayes_Section2_Fig.R
